| Россия |
Эквивалентность и порядок. Изоморфизмы
100. Докажите, что линейно упорядоченные
множества  и
и  (с
описанным выше порядком) не
изоморфны.
(с
описанным выше порядком) не
изоморфны.
101. Будут ли изоморфны линейно упорядоченные
множества  и
и  ?
?
102.Будут ли изоморфны линейно упорядоченные
множества  и
и  ?
?
Отображение 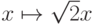 осуществляет изоморфизм между
интервалами
осуществляет изоморфизм между
интервалами 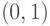 и
и  .
Но уже не так просто построить изоморфизм между
множествами рациональных точек этих интервалов (то есть
между
.
Но уже не так просто построить изоморфизм между
множествами рациональных точек этих интервалов (то есть
между  и
и  ),
поскольку
умножение на
),
поскольку
умножение на  переводит рациональные числа в
иррациональные. Тем не менее изоморфизм построить можно. Для
этого надо взять возрастающие последовательности рациональных чисел
переводит рациональные числа в
иррациональные. Тем не менее изоморфизм построить можно. Для
этого надо взять возрастающие последовательности рациональных чисел 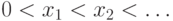 и
и 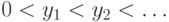 , сходящиеся
соответственно к
, сходящиеся
соответственно к  и
и  и построить кусочно -
линейную
функцию
и построить кусочно -
линейную
функцию  , которая переводит
, которая переводит  в
в  и линейна на каждом
из отрезков
и линейна на каждом
из отрезков ![[x_i,x_{i+1}]](/sites/default/files/tex_cache/ed75161bcea8dc1b8e616c48806cc6e7.png) (рис.7.1
).
Легко понять, что она будет искомым
изоморфизмом.
(рис.7.1
).
Легко понять, что она будет искомым
изоморфизмом.
103. Покажите, что множество рациональных чисел интервала 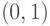 и
множество
и
множество  изоморфны. (Указание: здесь тоже
можно построить ломаную; впрочем, у этой задачи есть и другое решение,
которое начинается с того, что функция
изоморфны. (Указание: здесь тоже
можно построить ломаную; впрочем, у этой задачи есть и другое решение,
которое начинается с того, что функция 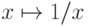 переводит
рациональные числа в рациональные.)
переводит
рациональные числа в рациональные.)
Более сложная конструкция требуется в следующей задаче (видимо, ничего проще, чем сослаться на общую теорему 13, тут не придумаешь).
104. Докажите, что множество двоично - рациональных чисел
интервала 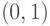 изоморфно множеству
изоморфно множеству  . (Число считается двоично - рациональным, если оно имеет вид
. (Число считается двоично - рациональным, если оно имеет вид 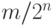 , где
, где  - целое число, а
- целое число, а  - натуральное.)
- натуральное.)
Два элемента  ,
,  линейно упорядоченного множества
называют соседними, если
линейно упорядоченного множества
называют соседними, если  и не
существует элемента между
ними, то есть такого
и не
существует элемента между
ними, то есть такого  , что
, что  . Линейно
упорядоченное
множество называют плотным,
если в нем нет соседних
элементов (то есть между любыми двумя есть третий).
. Линейно
упорядоченное
множество называют плотным,
если в нем нет соседних
элементов (то есть между любыми двумя есть третий).
Теорема 13. Любые два счетных плотных линейно упорядоченных множества без наибольшего и наименьшего элементов изоморфны.
Доказательство.
Пусть  и
и  - данные нам множества. Требуемый
изоморфизм
между ними строится по шагам. После
- данные нам множества. Требуемый
изоморфизм
между ними строится по шагам. После  шагов у нас есть два
шагов у нас есть два  - элементных подмножества
- элементных подмножества  и
и  ,
элементы которых мы будем называть " охваченными", и
взаимно однозначное соответствие между ними, сохраняющее
порядок. На очередном шаге мы берем какой - то неохваченный
элемент одного из
множеств (скажем, множества
,
элементы которых мы будем называть " охваченными", и
взаимно однозначное соответствие между ними, сохраняющее
порядок. На очередном шаге мы берем какой - то неохваченный
элемент одного из
множеств (скажем, множества  ) и сравниваем его со всеми
охваченными
элементами
) и сравниваем его со всеми
охваченными
элементами  . Он может оказаться либо меньше всех,
либо больше, либо попасть между какими - то двумя. В
каждом из случаев мы можем найти неохваченный элемент в
. Он может оказаться либо меньше всех,
либо больше, либо попасть между какими - то двумя. В
каждом из случаев мы можем найти неохваченный элемент в  ,
находящийся в том же положении (больше всех,
между первым и вторым
охваченным сверху,
между вторым и третьим
охваченным сверху и т.п.).
При этом мы пользуемся тем, что
в
,
находящийся в том же положении (больше всех,
между первым и вторым
охваченным сверху,
между вторым и третьим
охваченным сверху и т.п.).
При этом мы пользуемся тем, что
в  нет наименьшего элемента, нет наибольшего и нет соседних
элементов, - в зависимости от того, какой из трех случаев имеет
место. После этого мы добавляем выбранные элементы к
нет наименьшего элемента, нет наибольшего и нет соседних
элементов, - в зависимости от того, какой из трех случаев имеет
место. После этого мы добавляем выбранные элементы к 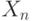 и
и 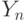 ,
считая их соответствующими друг другу.
,
считая их соответствующими друг другу.
Чтобы в пределе
получить изоморфизм между множествами  и
и  , мы
должны
позаботиться о том, чтобы все элементы обоих множеств были рано
или поздно охвачены. Это можно сделать так: поскольку каждое
из множеств счетно, пронумеруем его элементы и будем выбирать
неохваченный элемент с наименьшим номером (на нечетных шагах -
из
, мы
должны
позаботиться о том, чтобы все элементы обоих множеств были рано
или поздно охвачены. Это можно сделать так: поскольку каждое
из множеств счетно, пронумеруем его элементы и будем выбирать
неохваченный элемент с наименьшим номером (на нечетных шагах -
из  , на четных - из
, на четных - из  ). Это соображение завершает
доказательство.
). Это соображение завершает
доказательство.
105. Сколько существует неизоморфных счетных плотных
линейно упорядоченных множеств (про наименьший и наибольший
элементы ничего не известно). (Ответ:  .)
.)
106. Приведите пример двух плотных линейно упорядоченных множеств
мощности континуум без наименьшего и наибольшего элементов,
не являющихся изоморфными.
(Указание: возьмите множества  и
и  .)
.)
Теорема 14.
Всякое счетное линейно упорядоченное множество
изоморфно некоторому подмножеству множества  .
.
Доказательство.
Заметим сразу же, что вместо множества  можно было взять
любое плотное счетное всюду плотное множество без первого
и последнего элементов, так как они все изоморфны.
можно было взять
любое плотное счетное всюду плотное множество без первого
и последнего элементов, так как они все изоморфны.
Доказательство этого утверждения происходит так же, как и в теореме 13 - с той разницей, что новые необработанные элементы берутся только с одной стороны (из данного нам множества), а пары к ним подбираются в множестве рациональных чисел.
107. Дайте другое доказательство теоремы 14, заметив,
что любое множество  изоморфно подмножеству множества
изоморфно подмножеству множества  .
.