| Россия |
Функции
До сих пор мы старались ограничиваться минимумом формальностей и говорили о функциях, их аргументах, значениях, композиции и т.п. без попыток дать определения этих понятий. Сейчас мы дадим формальные определения.
Пусть  и
и  - два множества. Рассмотрим множество
всех
упорядоченных пар
- два множества. Рассмотрим множество
всех
упорядоченных пар 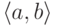 , где
, где 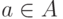 и
и 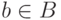 . Это множество называется декартовым
произведением множеств
. Это множество называется декартовым
произведением множеств  и
и  и
обозначается
и
обозначается  .
(К вопросу о том, что такое упорядоченная пара, мы еще вернемся)
.
(К вопросу о том, что такое упорядоченная пара, мы еще вернемся)
Любое подмножество  множества
множества  называется отношением между множествами
называется отношением между множествами  и
и  . Если
. Если 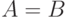 ,
говорят о бинарном отношении на
множестве
,
говорят о бинарном отношении на
множестве  .
Например, на множестве натуральных чисел можно рассмотреть
бинарное отношение " быть делителем", обычно обозначаемое
символом
.
Например, на множестве натуральных чисел можно рассмотреть
бинарное отношение " быть делителем", обычно обозначаемое
символом 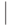 . Тогда можно в принципе было бы написать
. Тогда можно в принципе было бы написать  и
и 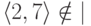 .
Обычно,
однако, знак отношения пишут между объектами (например,
.
Обычно,
однако, знак отношения пишут между объектами (например,  ).
).
59.Вопрос для самоконтроля: отношения " быть делителем" и " делиться на" - это одно и то же отношение или разные? (Ответ: конечно, разные - в упорядоченной паре порядок существен.)
Если аргументами функции являются элементы множества  , а
значениями - элементы множества
, а
значениями - элементы множества  , то можно рассмотреть
отношение между
, то можно рассмотреть
отношение между  и
и  , состоящее из пар
вида
, состоящее из пар
вида  . По аналогии с графиками функций на плоскости
такое множество можно назвать графиком функции
. По аналогии с графиками функций на плоскости
такое множество можно назвать графиком функции  . С формальной
точки зрения, однако,
удобнее не вводить отдельного неопределяемого
понятия функции, а вместо этого отождествить функцию с ее
графиком.
. С формальной
точки зрения, однако,
удобнее не вводить отдельного неопределяемого
понятия функции, а вместо этого отождествить функцию с ее
графиком.
Отношение  называется функцией
из
называется функцией
из  в
в  , если оно
не содержит
пар с одинаковым первым
членом и разными вторыми. Другими словами, это означает,
что для каждого
, если оно
не содержит
пар с одинаковым первым
членом и разными вторыми. Другими словами, это означает,
что для каждого 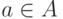 существует не более одного
существует не более одного  ,
при котором
,
при котором 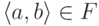 .
.
Те элементы 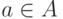 , для которых такое
, для которых такое  существует,
образуют область определения
функции
существует,
образуют область определения
функции  .
Она обозначается
.
Она обозначается  (от английского слова domain). Для любого элемента
(от английского слова domain). Для любого элемента 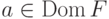 можно определить значение
функции
можно определить значение
функции  на аргументе
на аргументе  (" в точке
(" в точке  ", как иногда говорят) как тот
единственный элемент
", как иногда говорят) как тот
единственный элемент 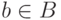 , для которого
, для которого 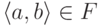 .
Этот элемент записывают как
.
Этот элемент записывают как 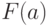 . Все такие
элементы
. Все такие
элементы  образуют множество значений
образуют множество значений 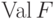 .
.
Если 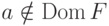 , то говорят, что функция не
определена
на
, то говорят, что функция не
определена
на  . Заметим, что по нашему определению функция из
. Заметим, что по нашему определению функция из  в
в  не обязана быть определена на всех элементах множества
не обязана быть определена на всех элементах множества  - ее
область определения может быть любым подмножеством
множества
- ее
область определения может быть любым подмножеством
множества  . Симметричным образом множество ее значений может
не совпадать с множеством
. Симметричным образом множество ее значений может
не совпадать с множеством  .
.
Если область определения функции  из
из  в
в  совпадает с
совпадает с  , то
пишут
, то
пишут 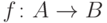 .
.
Пример: тождественная функция 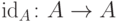 переводит множество
переводит множество  в себя, причем
в себя, причем 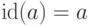 для
любого
для
любого 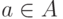 . Она представляет собой множество пар вида
. Она представляет собой множество пар вида  для всех
для всех 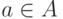 . (Индекс
. (Индекс  в
в 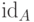 иногда опускают,
если ясно, о каком множестве идет речь.)
иногда опускают,
если ясно, о каком множестве идет речь.)
Композицией
двух функций 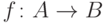 и
и 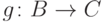 называют функцию
называют функцию 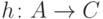 , определенную
соотношением
, определенную
соотношением 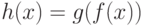 . Другими словами,
. Другими словами,  представляет собой
множество пар
представляет собой
множество пар 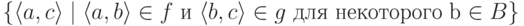 .
Композиция функций обозначается
.
Композиция функций обозначается 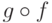 (мы, как и в
большинстве книг, пишем справа функцию, которая применяется
первой).
(мы, как и в
большинстве книг, пишем справа функцию, которая применяется
первой).
Очевидно, композиция (как операция над функциями)
ассоциативна, то есть  , поэтому в композиции нескольких подряд
идущих функций можно опускать скобки.
, поэтому в композиции нескольких подряд
идущих функций можно опускать скобки.
Пусть 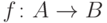 . Прообразом
подмножества
. Прообразом
подмножества  называется множество всех элементов
называется множество всех элементов 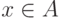 , для
которых
, для
которых  .
Оно обозначается
.
Оно обозначается 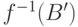 :
:

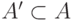 называется
множество всех
значений функции
называется
множество всех
значений функции  на всех элементах множества
на всех элементах множества 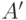 .
Оно
обозначается
.
Оно
обозначается 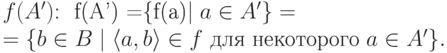
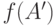 может привести к путанице (одни и
те же круглые скобки употребляются и для значения функции, и для
образа множества), но
обычно ясно, что имеется в виду.
может привести к путанице (одни и
те же круглые скобки употребляются и для значения функции, и для
образа множества), но
обычно ясно, что имеется в виду.60. Какие из следующих равенств верны?

(Здесь 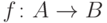 ,
, 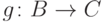 ,
, 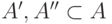 ,
,  ,
, 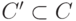 .)
.)
