| Россия |
Эквивалентность и порядок. Изоморфизмы
Отношения эквивалентности и порядка
Напомним, что бинарным отношением на множестве  называется
подмножество
называется
подмножество 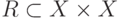 ; вместо
; вместо 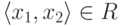 часто пишут
часто пишут  .
.
Бинарное отношение  на множестве
на множестве  называется отношением эквивалентности,
если выполнены следующие свойства:
называется отношением эквивалентности,
если выполнены следующие свойства:
- (рефлексивность)
 для
всех
для
всех 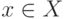 ;
; - (симметричность)
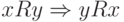 для всех
для всех  ;
; - (транзитивность)
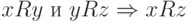 для любых элементов
для любых элементов 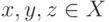 .
.
Имеет место следующее очевидное, но часто используемое утверждение:
Теорема 11.
(а)
Если множество  разбито в объединение непересекающихся
подмножеств, то отношение " лежать в одном подмножестве"
является отношением эквивалентности.
разбито в объединение непересекающихся
подмножеств, то отношение " лежать в одном подмножестве"
является отношением эквивалентности.
(б) Всякое отношение эквивалентности получается описанным способом из некоторого разбиения.
Доказательство.
Первое утверждение совсем очевидно; мы приведем доказательство
второго, чтобы было видно, где используются все пункты
определения эквивалентности. Итак, пусть  - отношение
эквивалентности. Для каждого элемента
- отношение
эквивалентности. Для каждого элемента 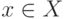 рассмотрим его класс эквивалентности - множество
всех
рассмотрим его класс эквивалентности - множество
всех 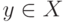 , для которых верно
, для которых верно 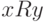 .
.
Докажем, что для двух различных  ,
,  такие
множества либо
не пересекаются, либо совпадают. Пусть они пересекаются, то есть
имеют общий элемент
такие
множества либо
не пересекаются, либо совпадают. Пусть они пересекаются, то есть
имеют общий элемент  . Тогда
. Тогда 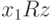 и
и 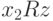 , откуда
, откуда 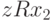 (симметричность) и
(симметричность) и  (транзитивность), а также
(транзитивность), а также 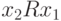 (симметричность). Поэтому для любого
(симметричность). Поэтому для любого  из
из 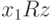 следует
следует 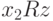 (транзитивность) и
наоборот.
(транзитивность) и
наоборот.
Осталось заметить, что в силу рефлексивности каждый элемент  принадлежит задаваемому им классу, то есть действительно
все множество
принадлежит задаваемому им классу, то есть действительно
все множество  разбито на непересекающиеся классы.
разбито на непересекающиеся классы.
78. Покажите, что требования симметричности и транзитивности можно
заменить одним: 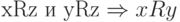 (при сохранении требования рефлексивности).
(при сохранении требования рефлексивности).
79. Сколько различных отношений эквивалентности существует на множестве 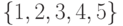 ?
?
80. На множестве  задано два отношения эквивалентности,
обозначаемые
задано два отношения эквивалентности,
обозначаемые 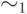 и
и  , имеющие
, имеющие  и
и 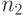 классов
эквивалентности соответственно.
Будет ли их пересечение
классов
эквивалентности соответственно.
Будет ли их пересечение ![x\sim y \hm\Leftrightarrow [(x\sim_1 y)\text{ и }(x\sim_2 y)]](/sites/default/files/tex_cache/79dfcbf567c926698592456ef0441bf7.png) отношением эквивалентности? Сколько у него может быть классов?
Что можно сказать про объединение отношений?
отношением эквивалентности? Сколько у него может быть классов?
Что можно сказать про объединение отношений?
81. (Теорема Рамсея)
Множество всех  - элементных подмножеств
бесконечного множества
- элементных подмножеств
бесконечного множества  разбито на
разбито на  классов
(
классов
(  ,
,  -
натуральные числа). Докажите, что найдется бесконечное множество
-
натуральные числа). Докажите, что найдется бесконечное множество 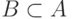 , все
, все  - элементные подмножества
которого
принадлежат одному классу.
- элементные подмножества
которого
принадлежат одному классу.
(При 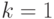 это очевидно: если бесконечное множество разбито
на конечное число классов, то один из классов бесконечен. При
это очевидно: если бесконечное множество разбито
на конечное число классов, то один из классов бесконечен. При  и
и  утверждение можно сформулировать так:
из бесконечного множества людей можно выбрать либо
бесконечно много попарно знакомых, либо бесконечно много
попарно незнакомых. Конечный вариант этого утверждения - о том,
что среди любых шести людей есть либо три попарно знакомых,
либо три попарно незнакомых, - известная задача для школьников.)
утверждение можно сформулировать так:
из бесконечного множества людей можно выбрать либо
бесконечно много попарно знакомых, либо бесконечно много
попарно незнакомых. Конечный вариант этого утверждения - о том,
что среди любых шести людей есть либо три попарно знакомых,
либо три попарно незнакомых, - известная задача для школьников.)
Множество классов эквивалентности называют фактор -
множеством
множества  по отношению эквивалентности
по отношению эквивалентности  .
(Если отношение согласовано с дополнительными структурами
на
.
(Если отношение согласовано с дополнительными структурами
на  , получаются фактор - группы, фактор - кольца и т.д)
, получаются фактор - группы, фактор - кольца и т.д)
Отношения эквивалентности нам не раз еще встретятся, но сейчас наша основная тема - отношения порядка.
Бинарное отношение  на множестве
на множестве  называется отношением
частичного порядка,
если выполнены такие свойства:
называется отношением
частичного порядка,
если выполнены такие свойства:
(Следуя традиции, мы используем символ  (а не букву) как знак
отношения порядка.) Множество с заданным на нем отношением частичного
порядка называют частично упорядоченным.
(а не букву) как знак
отношения порядка.) Множество с заданным на нем отношением частичного
порядка называют частично упорядоченным.
Говорят, что два элемента 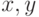 частично упорядоченного
множества сравнимы,
если
частично упорядоченного
множества сравнимы,
если  или
или  . Заметим,
что определение частичного порядка не требует, чтобы любые два
элемента множества были сравнимы. Добавив это требование, мы получим
определение линейного порядка ( линейно упорядоченного
множества ).
. Заметим,
что определение частичного порядка не требует, чтобы любые два
элемента множества были сравнимы. Добавив это требование, мы получим
определение линейного порядка ( линейно упорядоченного
множества ).
Приведем несколько примеров частичных порядков:
- Числовые множества с обычным отношением порядка (здесь порядок будет линейным).
- На множестве
 всех пар
действительных
чисел можно ввести частичный порядок, считая, что
всех пар
действительных
чисел можно ввести частичный порядок, считая, что 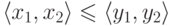 , если
, если  и
и  . Этот порядок уже не будет линейным: пары
. Этот порядок уже не будет линейным: пары 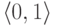 и
и 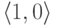 не сравнимы.
не сравнимы. - На множестве функций с действительными аргументами и значениями
можно ввести частичный порядок, считая, что
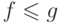 , если
, если 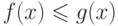 при всех
при всех 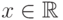 . Этот порядок не
будет
линейным.
. Этот порядок не
будет
линейным. - На множестве целых положительных чисел можно определить порядок,
считая, что
 , если
, если  делит
делит  .
Этот порядок
тоже не будет линейным.
.
Этот порядок
тоже не будет линейным. - Отношение " любой простой делитель числа
 является также и
делителем
числа
является также и
делителем
числа  " не будет отношением порядка на множестве целых
положительных чисел (оно рефлексивно и транзитивно, но не
антисимметрично).
" не будет отношением порядка на множестве целых
положительных чисел (оно рефлексивно и транзитивно, но не
антисимметрично). - Пусть
 - произвольное множество. Тогда на
множестве
- произвольное множество. Тогда на
множестве 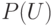 всех
подмножеств множества
всех
подмножеств множества  отношение включения
отношение включения  будет
частичным порядком.
будет
частичным порядком. - На буквах русского алфавита традиция определяет некоторый
порядок
(
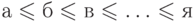 ).
Этот порядок линеен - про любые две буквы можно сказать, какая из
них раньше (при необходимости заглянув в словарь).
).
Этот порядок линеен - про любые две буквы можно сказать, какая из
них раньше (при необходимости заглянув в словарь). - На словах русского алфавита определен лексикографический
порядок (как в словаре). Формально определить его можно так:
если слово
 является началом слова
является началом слова  , то
, то  (например,
(например, 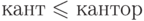 ). Если ни одно из слов
не является началом другого, посмотрим на первую по порядку
букву, в которой слова отличаются: то слово, где эта буква
меньше в алфавитном порядке, и будет меньше. Этот порядок также
линеен (иначе что бы делали составители словарей?).
). Если ни одно из слов
не является началом другого, посмотрим на первую по порядку
букву, в которой слова отличаются: то слово, где эта буква
меньше в алфавитном порядке, и будет меньше. Этот порядок также
линеен (иначе что бы делали составители словарей?). - Отношение равенства (
 )
также является отношением частичного порядка, для которого
никакие два различных элемента не сравнимы.
)
также является отношением частичного порядка, для которого
никакие два различных элемента не сравнимы. - Приведем теперь бытовой пример. Пусть есть множество
 картонных
коробок. Введем на нем порядок, считая, что
картонных
коробок. Введем на нем порядок, считая, что  , если коробка
, если коробка  целиком помещается внутрь
коробки
целиком помещается внутрь
коробки  (или
если
(или
если  и
и  - одна и та же коробка). В зависимости от
набора
коробок этот порядок может быть или не быть линейным.
- одна и та же коробка). В зависимости от
набора
коробок этот порядок может быть или не быть линейным.
Пусть 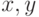 - элементы частично упорядоченного
множества
- элементы частично упорядоченного
множества  .
Говорят, что
.
Говорят, что 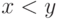 , если
, если  и
и  . Для этого отношения
выполнены такие
свойства:
. Для этого отношения
выполнены такие
свойства:
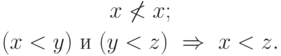
 и
и  , то есть
, то есть  ,
,  ,
,  ,
,  , то
, то  по
транзитивности; если бы оказалось, что
по
транзитивности; если бы оказалось, что 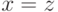 , то мы бы имели
, то мы бы имели 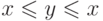 и потому
и потому 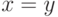 по
антисимметричности, что
противоречит предположению.)
по
антисимметричности, что
противоречит предположению.)Терминологическое замечание: мы читаем знак  как " меньше
или равно", а знак
как " меньше
или равно", а знак  - как " меньше", неявно
предполагая, что
- как " меньше", неявно
предполагая, что  тогда и только тогда, когда
тогда и только тогда, когда  или
или 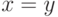 .
К счастью, это действительно так. Еще одно замечание: выражение
.
К счастью, это действительно так. Еще одно замечание: выражение  ("
("  больше
больше  ") означает,
что
") означает,
что 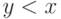 ,
а выражение
,
а выражение  ("
("  больше или
равно
больше или
равно  ") означает,
что
") означает,
что  .
.

 для
всех
для
всех  для всех
для всех  для всех
для всех