| Россия |
Эквивалентность и порядок. Изоморфизмы
82. Объясните, почему не стоит читать  как "
как "  не больше
не больше  ".
".
В некоторых книжках отношение частичного порядка определяется
как отношение  , удовлетворяющее двум указанным свойствам. В
этом случае отношение
, удовлетворяющее двум указанным свойствам. В
этом случае отношение ![x\hm\le y \hm\Leftrightarrow [(x\hm<y)
\text{ или } (x\hm=y)]](/sites/default/files/tex_cache/1329dab11cabbc5ffb57a24b0650a2eb.png) является отношением частичного порядка в
смысле нашего определения.
является отношением частичного порядка в
смысле нашего определения.
83.Проверьте это.
Во избежание путаницы отношение  иногда называют отношением строгого порядка, а отношение
иногда называют отношением строгого порядка, а отношение  - отношением нестрогого порядка. Одно и то же частично упорядоченное
множество можно задавать по - разному: можно сначала определить
отношение нестрогого порядка
- отношением нестрогого порядка. Одно и то же частично упорядоченное
множество можно задавать по - разному: можно сначала определить
отношение нестрогого порядка  (рефлексивное,
антисимметричное и транзитивное) и затем из него получить
отношение строгого порядка
(рефлексивное,
антисимметричное и транзитивное) и затем из него получить
отношение строгого порядка  , а можно действовать и наоборот.
, а можно действовать и наоборот.
84. Опуская требование антисимметричности в определении частичного порядка,
получаем определение предпорядка.
Докажите, что любой
предпорядок устроен так: множество делится на непересекающиеся
классы, при этом  для любых двух элементов
для любых двух элементов  ,
,  из одного класса, а на фактор - множестве задан
частичный
порядок, который и определяет результат сравнения двух элементов
из разных классов.
из одного класса, а на фактор - множестве задан
частичный
порядок, который и определяет результат сравнения двух элементов
из разных классов.
Вот несколько конструкций, позволяющих строить одни упорядоченные множества из других.
- Пусть
 - подмножество частично упорядоченного
множества
- подмножество частично упорядоченного
множества  .
Тогда на множестве
.
Тогда на множестве  возникает естественный частичный порядок, индуцированный из
возникает естественный частичный порядок, индуцированный из  .
Формально говоря,Если порядок на
.
Формально говоря,Если порядок на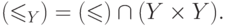
 был линейным, то и индуцированный порядок
на
был линейным, то и индуцированный порядок
на  ,
очевидно, будет линейным.
,
очевидно, будет линейным. - Пусть
 и
и  - два непересекающихся частично
упорядоченных множества. Тогда на их объединении можно
определить частичный порядок так: внутри каждого множества
элементы сравниваются как раньше, а любой элемент
множества
- два непересекающихся частично
упорядоченных множества. Тогда на их объединении можно
определить частичный порядок так: внутри каждого множества
элементы сравниваются как раньше, а любой элемент
множества  по определению меньше любого элемента
по определению меньше любого элемента  .
Это
множество естественно обозначить
.
Это
множество естественно обозначить  .
(Порядок будет
линейным, если он был таковым на каждом из множеств.)
.
(Порядок будет
линейным, если он был таковым на каждом из множеств.)Это же обозначение применяют и для пересекающихся (и даже совпадающих множеств). Например, говоря об упорядоченном множестве
 , мы берем две
непересекающиеся копии натурального ряда
, мы берем две
непересекающиеся копии натурального ряда  и
и 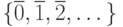 и рассматриваем
множество
и рассматриваем
множество 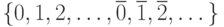 , причем
, причем  при всех
при всех  и
и  , а внутри каждой копии порядок
обычный.
, а внутри каждой копии порядок
обычный. - Пусть
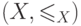 и
и 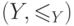 - два
упорядоченных
множества. Можно определить порядок на произведении
- два
упорядоченных
множества. Можно определить порядок на произведении  несколькими
способами. Можно считать, что
несколькими
способами. Можно считать, что 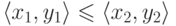 , если
, если  и
и  (покоординатное сравнение). Этот порядок, однако, не будет
линейным, даже если исходные порядки и были линейными: если
первая координата больше у одной пары, а вторая у другой, как их
сравнить? Чтобы получить линейный
порядок, договоримся, какая координата будет " главной" и
будем сначала сравнивать по ней, а потом (в случае равенства) -
по другой. Если главной считать
(покоординатное сравнение). Этот порядок, однако, не будет
линейным, даже если исходные порядки и были линейными: если
первая координата больше у одной пары, а вторая у другой, как их
сравнить? Чтобы получить линейный
порядок, договоримся, какая координата будет " главной" и
будем сначала сравнивать по ней, а потом (в случае равенства) -
по другой. Если главной считать  - координату, то
- координату, то  , если
, если  или если
или если  , а
, а  . Однако по
техническим
причинам удобно считать главной вторую координату. Говоря о
произведении двух линейно упорядоченных множеств как о линейно
упорядоченном множестве, мы в дальнейшем подразумеваем именно
такой порядок (сначала сравниваем по второй координате).
. Однако по
техническим
причинам удобно считать главной вторую координату. Говоря о
произведении двух линейно упорядоченных множеств как о линейно
упорядоченном множестве, мы в дальнейшем подразумеваем именно
такой порядок (сначала сравниваем по второй координате).
85. Докажите, что в частично упорядоченном
множестве  (порядок покоординатный)
нет бесконечного
подмножества, любые два элемента
которого были бы несравнимы. Верно ли аналогичное
утверждение для
(порядок покоординатный)
нет бесконечного
подмножества, любые два элемента
которого были бы несравнимы. Верно ли аналогичное
утверждение для  ?
?
86. Докажите аналогичное утверждение для 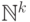 (порядок
покоординатный).
(порядок
покоординатный).
87. Пусть  - конечное множество из
- конечное множество из  элементов.
Рассмотрим
множество
элементов.
Рассмотрим
множество 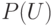 всех подмножеств множества
всех подмножеств множества  ,
упорядоченное
по включению. Какова максимально
возможная мощность множества
,
упорядоченное
по включению. Какова максимально
возможная мощность множества  , если
индуцированный на
, если
индуцированный на  порядок линеен? если никакие два
элемента
порядок линеен? если никакие два
элемента  не сравнимы? (Указание: см. задачу 14.)
не сравнимы? (Указание: см. задачу 14.)
88. Сколько существует различных линейных порядков на
множестве из  элементов?
элементов?
89. Докажите, что всякий частичный порядок на конечном множестве
можно продолжить до линейного (" продолжить" означает, что
если  в исходном порядке, то и в новом это останется
так).
в исходном порядке, то и в новом это останется
так).
90. Дано бесконечное частично упорядоченное множество  . Докажите,
что в нем всегда найдется либо бесконечное подмножество попарно
несравнимых элементов, либо бесконечное подмножество, на котором
индуцированный порядок линеен.
. Докажите,
что в нем всегда найдется либо бесконечное подмножество попарно
несравнимых элементов, либо бесконечное подмножество, на котором
индуцированный порядок линеен.
91. (Конечный вариант предыдущей задачи.) Даны целые положительные числа  и
и  . Докажите, что во всяком частично
упорядоченном множестве
мощности
. Докажите, что во всяком частично
упорядоченном множестве
мощности  можно указать либо
можно указать либо 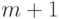 попарно
несравнимых
элементов, либо
попарно
несравнимых
элементов, либо  попарно сравнимых.
попарно сравнимых.
92. В строчку написаны  различных чисел. Докажите, что можно
часть из них вычеркнуть так, чтобы осталась либо возрастающая
последовательность длины
различных чисел. Докажите, что можно
часть из них вычеркнуть так, чтобы осталась либо возрастающая
последовательность длины 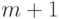 , либо убывающая
последовательность длины
, либо убывающая
последовательность длины  . (Указание: можно воспользоваться
предыдущей задачей.)
. (Указание: можно воспользоваться
предыдущей задачей.)
93. Рассмотрим семейство всех подмножеств натурального ряда, упорядоченное по включению. Существует ли у него линейно упорядоченное (в индуцированном порядке) подсемейство мощности континуум? Существует ли у него подсемейство мощности континуум, любые два элемента которого несравнимы?
Элемент частично упорядоченного множества называют наибольшим, если он больше любого другого элемента, и максимальным, если не существует большего элемента. Если множество не является линейно упорядоченным, то это не одно и то же: наибольший элемент автоматически является максимальным, но не наоборот. (Одно дело коробка, в которую помещается любая другая, другое - коробка, которая никуда больше не помещается.)
Аналогичным образом определяются наименьшие и минимальные элементы.
Легко понять, что наибольший элемент в данном частично упорядоченном множестве может быть только один, в то время как максимальных элементов может быть много.
94. Докажите, что любые два максимальных элемента
не сравнимы. Докажите, что в конечном частично
упорядоченном множестве  для любого элемента
для любого элемента  найдется максимальный элемент
найдется максимальный элемент  , больший или
равный
, больший или
равный  .
.
