|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Нечеткие алгоритмы обучения
Алгоритм формирования нечеткого отношения предпочтения
Пусть  — множество таких альтернатив, что каждое
— множество таких альтернатив, что каждое 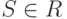 характеризуется
набором оценок по
характеризуется
набором оценок по  признакам:
признакам: 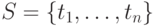 , и пусть
, и пусть  —
семейство всех непустых конечных подмножеств множества
—
семейство всех непустых конечных подмножеств множества  .
Для некоторого
.
Для некоторого 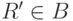 известно подмножество выбранных
альтернатив
известно подмножество выбранных
альтернатив 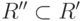 , т.е. для любых
, т.е. для любых 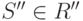 и
и 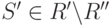 имеет место доминирование
имеет место доминирование  .
Предварительно, при анализе исходного множества альтернатив, сформирован
эталонный набор нечетких оценок
.
Предварительно, при анализе исходного множества альтернатив, сформирован
эталонный набор нечетких оценок  .
Значения функции принадлежности нечеткой оценки
.
Значения функции принадлежности нечеткой оценки 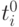 указывают на степень
близости значений
указывают на степень
близости значений  -го признака к значениям, определяющим
идеальную
альтернативу. Используя множество предпочтений
-го признака к значениям, определяющим
идеальную
альтернативу. Используя множество предпочтений
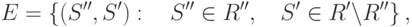
 .
.Пример.
Рассмотрим задачу выбора для рыболовецкого судна рационального
района промысла с учетом следующих показателей: 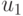 —
время
перехода в район лова,
—
время
перехода в район лова, 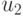 — прогноз вылова,
— прогноз вылова, 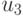 —
стоимостная характеристика прогнозируемого объекта лова,
—
стоимостная характеристика прогнозируемого объекта лова,  —
гидрометеоусловия. Показатели, в сущности, играют роль лингвистических
переменных.
—
гидрометеоусловия. Показатели, в сущности, играют роль лингвистических
переменных.
Лицу, принимающему решение, предложены
альтернативы  —
— 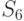 (см.табл.12.1). Пусть
выбрана
альтернатива
(см.табл.12.1). Пусть
выбрана
альтернатива  . Для обучения формируются две таблицы:
. Для обучения формируются две таблицы:
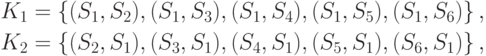
| U1 | U2 | U3 | U4 | U1 | U2 | U3 | U4 | ||
| S1 | хор. | хор. | хор. | уд. | S1 | плох. | хор. | плох. | уд. |
| S2 | оч. хор. | плох. | хор. | уд. | S2 | уд. | хор. | хор. | неуд. |
| S3 | оч. хор. | хор. | хор. | неуд. | S3 | плох. | хор. | хор. | уд. |
| S4 | уд. | хор. | хор. | уд. | S4 | уд. | хор. | норм. | уд. |
| S5 | оч. плох. | хор. | хор. | уд. | S5 | уд. | норм. | норм. | уд. |
| S6 | хор. | норм. | плох. | уд. | S6 |
Для каждой пары наборов 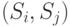 вычисляются оценки
сравнения
вычисляются оценки
сравнения  -го
элемента первого набора с
-го
элемента первого набора с  -м элементом второго набора:
-м элементом второго набора:

 определяет конкретный оператор, например, нечеткую
меру сходства.
определяет конкретный оператор, например, нечеткую
меру сходства.В результате получаются две таблицы наборов нечетких оценок поэлементного сравнения. На основе полученных таблиц, используя логические операторы и логические функции двух переменных, выделяются полезные признаки и минимальный базис. Содержательное значение утверждения, соответствующего минимальному базису, следующее:
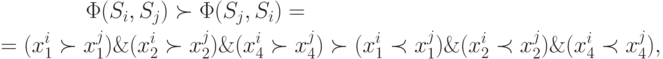
 — лингвистическое значение
— лингвистическое значение  -го показателя,
-го показателя,  —
логический признак. Физический смысл приведенного утверждения:
район
—
логический признак. Физический смысл приведенного утверждения:
район  предпочтительнее района
предпочтительнее района 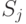 , если
утверждение [(время перехода до
, если
утверждение [(время перехода до  "меньше",
чем до
"меньше",
чем до 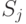 ), и (прогноз вылова в
), и (прогноз вылова в  "больше", чем в
"больше", чем в 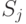 ), и (погодные
условия в
), и (погодные
условия в  "лучше", чем в
"лучше", чем в 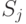 )]
более истинно, чем обратное
утверждение [(время перехода до
)]
более истинно, чем обратное
утверждение [(время перехода до  "больше", чем
до
"больше", чем
до 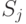 ), и (прогноз
вылова в
), и (прогноз
вылова в  "меньше", чем в
"меньше", чем в 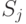 ), и
(погодные условия в
), и
(погодные условия в  "хуже",
чем в
"хуже",
чем в 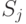 )].
)].Далее предположим, что среди неизвестных ситуаций 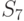 -
- 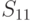 (табл. 12.1)
необходимо выбрать лучшую альтернативу, используя минимальный базис.
В табл. 12.2 изображена матрица предпочтений
(табл. 12.1)
необходимо выбрать лучшую альтернативу, используя минимальный базис.
В табл. 12.2 изображена матрица предпочтений  ,
элементы которой вычислялись посредством гарантированной оценки
,
элементы которой вычислялись посредством гарантированной оценки
![\[
\mu ^{ij} (K_1 ) = \mathop {\max }\limits_{v \in [0,1]} \;\mu _{H_1 (S_i ,S_j
)} (v),](/sites/default/files/tex_cache/3f8056fd49bac37de45af1d3ad907682.png)
| S7 | S8 | S9 | S10 | S11 | |
|---|---|---|---|---|---|
| S7 | 0,88 0,38 | 1 0,38 | 0,88 0,38 | 0,88 0,38 | |
| S8 | 0,75 1 | 0,75 1 | 0,75 1 | 0,75 1 | |
| S9 | 1 0,38 | 0,88 0,38 | 0,88 0,38 | 0,88 0,38 | |
| S10 | 1 0,38 | 1 0,38 | 1 0,38 | 1 0,38 | |
| S11 | 0,88 0,38 | 0,88 0,38 | 0,88 0,38 | 0,88 0,38 |
 — значение
— значение  -го признака на паре
альтернатив
-го признака на паре
альтернатив 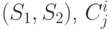 — значение
— значение  -го
признака на парах
альтернатив
-го
признака на парах
альтернатив  -го класса (
-го класса ( 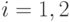 ). Каждый элемент
матрицы содержит два значения.
Левое значение указывает степень, с которой
). Каждый элемент
матрицы содержит два значения.
Левое значение указывает степень, с которой  доминирует над
доминирует над 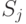 .
Правое значение указывает степень, с которой
.
Правое значение указывает степень, с которой 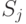 доминирует над
доминирует над  .
Для построения нечеткого графа предпочтений альтернатив (рис.12.5)
используется следующее правило определения отношения доминирования
.
Для построения нечеткого графа предпочтений альтернатив (рис.12.5)
используется следующее правило определения отношения доминирования  :
: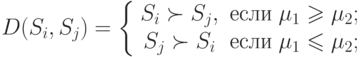

Согласно рис. 12.5, 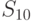 является недоминируемой
альтернативой, т.е.
не существует альтернативы, которая с ненулевой степенью доминирует над
является недоминируемой
альтернативой, т.е.
не существует альтернативы, которая с ненулевой степенью доминирует над 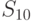 .
.

