|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Нечеткая логика
В сочетании слов "нечеткий" и "логика" есть что-то необычное. Логика в обычном смысле слова есть представление механизмов мышления, то, что никогда не может быть нечетким, но всегда строгим и формальным. Однако математики, исследовавшие эти механизмы мышления, заметили, что в действительности существует не одна логика (например, булева), а столько, сколько мы пожелаем, потому что все определяется выбором соответствующей системы аксиом. Конечно, как только аксиомы выбраны, все утверждения, построенные на их основе, должны быть строго, без противоречий увязаны друг с другом согласно правилам, установленным в этой системе аксиом.
Человеческое мышление — это совмещение интуиции и строгости, которое, с одной стороны, рассматривает мир в целом или по аналогии, а с другой стороны — логически и последовательно и, значит, представляет собой нечеткий механизм. Законы мышления, которые мы захотели бы включить в программы компьютеров, должны быть обязательно формальными; законы мышления, проявляемые в диалоге человека с человеком — нечеткие. Можем ли мы поэтому утверждать, что нечеткая логика может быть хорошо приспособлена к человеческому диалогу? Да — если математическое обеспечение, разработанное с учетом нечеткой логики, станет операционным и сможет быть технически реализовано, то человеко-машинное общение станет намного более удобным, быстрым и лучше приспособленным к решению проблем.
Термин " нечеткая логика " используется обычно в двух различных значениях. В узком смысле, нечеткая логика — это логическое исчисление, являющееся расширением многозначной логики. В ее широком смысле, который сегодня является преобладающим в использовании, нечеткая логика равнозначна теории нечетких множеств. С этой точки зрения, нечеткая логика в узком смысле является разделом нечеткой логики в широком смысле.
Определение. Любая нечеткая переменная характеризуется тройкой
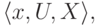
 — название переменной,
— название переменной,  —
универсальное множество,
—
универсальное множество,  —
нечеткое подмножество множества
—
нечеткое подмножество множества  , представляющее собой нечеткое
ограничение
на значение переменной
, представляющее собой нечеткое
ограничение
на значение переменной 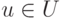 , обусловленное
, обусловленное  .
.Используя аналогию с саквояжем, нечеткую переменную можно уподобить
саквояжу с ярлыком, имеющим "мягкие" стенки. Тогда  — надпись на ярлыке
(название саквояжа),
— надпись на ярлыке
(название саквояжа),  — список предметов, которые в
принципе можно
поместить в саквояж, а
— список предметов, которые в
принципе можно
поместить в саквояж, а  — часть этого списка, где для
каждого предмета
— часть этого списка, где для
каждого предмета  указано число
указано число 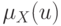 , характеризующее степень легкости, с
которой предмет
можно поместить в саквояж
, характеризующее степень легкости, с
которой предмет
можно поместить в саквояж  .
.
Рассмотрим теперь различные подходы к определению основных операций над нечеткими
переменными, а именно конъюнкции, дизъюнкции и отрицания. Данные
операции
являются основными для нечеткой логики в том смысле,
что все ее конструкции основываются на этих операциях. В настоящее время в нечеткой
логике в качестве операций конъюнкции и дизъюнкции широко используют  -нормы и
-нормы и  -конормы,
пришедшие в нечеткую
логику из теории вероятностных метрических
пространств. Они достаточно хорошо изучены и лежат в основе многих формальных
построений нечеткой
логики. В то же время расширение области приложений нечеткой
логики и возможностей нечеткого моделирования вызывает
необходимость обобщения этих операций. Одно направление связано с ослаблением
их аксиоматики с целью расширения инструментария нечеткого моделирования.
Другое направление обобщения операций конъюнкции и дизъюнкции нечеткой логики
связано с заменой множества значений принадлежности
-конормы,
пришедшие в нечеткую
логику из теории вероятностных метрических
пространств. Они достаточно хорошо изучены и лежат в основе многих формальных
построений нечеткой
логики. В то же время расширение области приложений нечеткой
логики и возможностей нечеткого моделирования вызывает
необходимость обобщения этих операций. Одно направление связано с ослаблением
их аксиоматики с целью расширения инструментария нечеткого моделирования.
Другое направление обобщения операций конъюнкции и дизъюнкции нечеткой логики
связано с заменой множества значений принадлежности ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) на
линейно или частично
упорядоченное множество лингвистических оценок правдоподобности. Эти обобщения
основных
операций нечеткой
логики, с одной стороны, вызываются необходимостью
разработки экспертных систем, в которых значения истинности фактов и правил
описываются экспертом или пользователем непосредственно в лингвистической
шкале и носят
качественный характер. С другой стороны, такие обобщения вызываются смещением
направления активного развития нечеткой логики от моделирования
количественных процессов, поддающихся измерению, к моделированию процессов
мышления человека, где восприятие мира и принятие решений происходит на основе
гранулирования информации и вычисления словами.
на
линейно или частично
упорядоченное множество лингвистических оценок правдоподобности. Эти обобщения
основных
операций нечеткой
логики, с одной стороны, вызываются необходимостью
разработки экспертных систем, в которых значения истинности фактов и правил
описываются экспертом или пользователем непосредственно в лингвистической
шкале и носят
качественный характер. С другой стороны, такие обобщения вызываются смещением
направления активного развития нечеткой логики от моделирования
количественных процессов, поддающихся измерению, к моделированию процессов
мышления человека, где восприятие мира и принятие решений происходит на основе
гранулирования информации и вычисления словами.
Естественным обобщением инволютивных операций отрицания нечеткой логики являются неиволютивные отрицания. Они представляют самостоятельный интерес и рассматриваются в нечеткой и других неклассических логиках. Необходимость исследования подобных операций отрицания вызывается также введением в рассмотрение обобщенных операций конъюнкции и дизъюнкции, связанных друг с другом с помощью операции отрицания.
