|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Опубликован: 26.07.2006 | Уровень: специалист | Доступ: свободно
Лекция 7:
Нечеткие числа и операции над ними
Аннотация: В лекции дается определение нечеткого
числа, рассматриваются его свойства, описываются операции над нечеткими
числами.
Подробно рассматриваются нечеткие треугольные числа, а также различные
арифметики
нечетких треугольных чисел.
Ключевые слова: нечеткое число, подмножество, принцип обобщения, операции, сложение, умножение, анализ, нечеткое число (L-R)-типа, функция принадлежности, коэффициенты, значение, нечеткое трапезоидное число, параметр, высказывание, нечеткое треугольное число, определение, landmark, вычисление, обратный, место, монотонно возрастающей, монотонно убывающей, пространство, бинарная операция, единица, алгебраические системы, группа, поле, функция, мощность, множества, нечеткое множество, равенство, алгоритм, арифметическое выражение
Основные определения
Нечеткое число — это нечеткое подмножество универсального множества действительных чисел, имеющее нормальную и выпуклую функцию принадлежности, то есть такую, что: а) существует значение носителя, в котором функция принадлежности равна единице, а также b) при отступлении от своего максимума влево или вправо функция принадлежности не возрастает.
Нечеткое
число 
унимодально, если условие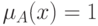 
справедливо только для одной точки действительной оси.
Выпуклое нечеткое
число называется нечетким нулем, если
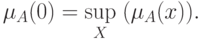
Подмножество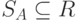 
называется носителем нечеткого
числа ,
если
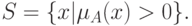
Нечеткое
число положительно, если 
,
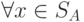
и отрицательно, если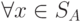 
.
Согласно принципу обобщения Заде было введено понятие арифметических
операций на множестве нечетких чисел. Для произвольных нечетких
чисел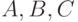 
и для любых чисел 
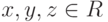справедливо
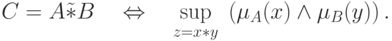
Расширенные бинарные арифметические операции (сложение, умножение и пр.) для нечетких чисел определяются через соответствующие операции для четких чисел с использованием принципа обобщения следующим образом:
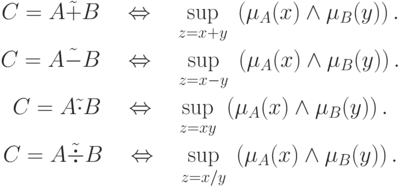
Анализ свойств арифметических операций над нечеткими числами показал, что нечеткое число не имеет противоположного и обратного чисел, сложение и умножение коммутативны, ассоциативны и в общем случае недистрибутивны.
При решении задач математического моделирования нечетких систем можно использовать нечеткие числа (L-R)-типа, которые предполагают более простую интерпретацию расширенных бинарных отношений.
Владимир Власов
