|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Лекция 4: Показатель размытости нечетких множеств. Нечеткие меры и интегралы
Как уже говорилось в прошлых лекциях, нечеткие множества используются для описания плохо определенных, неоднозначно понимаемых ситуаций, объектов, понятий. Де Лука предложил ввести в рассмотрение показатель этой неопределенности, который можно было бы использовать для оценки, классификации объектов, описываемых нечеткими множествами. Он же сформулировал основные свойства, которым должен удовлетворять такой показатель, называемый показателем размытости (или мерой энтропии) нечетких множеств, и в качестве этого показателя был предложен функционал, аналогичный шенноновской энтропии в теории информации. В настоящее время рассматриваются различные альтернативные подходы к определению показателя размытости нечеткого множества, обсуждаются его свойства и возможные приложения.
Можно выделить несколько аспектов, связанных с понятием показателя размытости нечеткого множества. Прежде всего, это — интерпретация показателя размытости как показателя внутренней неопределенности, двусмысленности, противоречивости, обусловленных неполной, частичной принадлежностью объектов множеству. Второй аспект связан с интерпретацией показателя размытости как меры отличия нечеткого множества от обычного множества. И наконец, само существование нетривиального показателя размытости, удовлетворяющего определенным свойствам, напрямую зависит от свойств алгебры нечетких множеств и характеризует ее как алгебраическую структуру. В соответствии с этими тремя аспектами и будут рассмотрены основные результаты, связанные с понятием показателя размытости.
Аксиоматический подход к определению показателя размытости нечеткого множества
Показатель
размытости нечеткого множества можно определить как меру внутренней
неопределенности, двусмысленности объектов множества  по
отношению к некоторому
свойству
по
отношению к некоторому
свойству  , характеризующему эти объекты и определяющему в
, характеризующему эти объекты и определяющему в  нечеткое множество
объектов
нечеткое множество
объектов  . Если некоторый объект
. Если некоторый объект 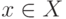 обладает свойством
обладает свойством  , но
лишь в частичной мере:
, но
лишь в частичной мере: 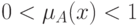 , то внутренняя
неопределенность,
двусмысленность объекта
, то внутренняя
неопределенность,
двусмысленность объекта  по отношению к свойству
по отношению к свойству  проявляется в том,
что он, хотя и в разной степени, принадлежит сразу двум противоположным
классам:
классу объектов, "обладающих свойством
проявляется в том,
что он, хотя и в разной степени, принадлежит сразу двум противоположным
классам:
классу объектов, "обладающих свойством  ", и классу
объектов, "не обладающих
свойством
", и классу
объектов, "не обладающих
свойством  ". Эта двусмысленность объекта
". Эта двусмысленность объекта  по
отношению к свойству
по
отношению к свойству  максимальна, когда степени принадлежности объекта
максимальна, когда степени принадлежности объекта  к обоим
классам
равны, т.е.
к обоим
классам
равны, т.е. 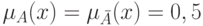 . И наоборот,
двусмысленность объекта минимальна, когда объект принадлежит только к одному
из этих классов, т.е. либо
. И наоборот,
двусмысленность объекта минимальна, когда объект принадлежит только к одному
из этих классов, т.е. либо 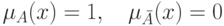 , либо
, либо 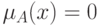 ,
, 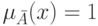 . Таким
образом, глобальный показатель размытости нечеткого множества
. Таким
образом, глобальный показатель размытости нечеткого множества  можно
определить в виде функционала
можно
определить в виде функционала  , удовлетворяющего следующим
условиям:
, удовлетворяющего следующим
условиям:
P1. 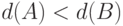 , если
, если  является заострением
является заострением  ,
т.е.
,
т.е. 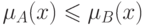 при
при  при
при 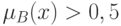 и
и 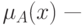 любое при
любое при 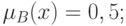
P2. 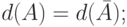
P3. Если 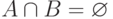 , то
, то 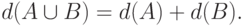
Итак, показатель
размытости можно рассматривать как аддитивный,
симметричный и строго возрастающий с увеличением размытости нечеткого
множества функционал, определенный на множестве 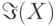 всех
нечетких подмножеств множества
всех
нечетких подмножеств множества  .
.
Можно доказать, что вещественный, определенный на 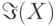 функционал
является показателем размытости тогда и только тогда,
если он допускает представление
функционал
является показателем размытости тогда и только тогда,
если он допускает представление
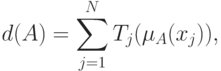
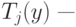 вещественнозначные функции от
вещественнозначные функции от ![\(y \in [0,1]\)](/sites/default/files/tex_cache/aba1bdaa425fce9885143b43e584d356.png) такие, что
такие, что  строго возрастает на интервале
строго возрастает на интервале ![[0, 0,5]](/sites/default/files/tex_cache/2784fda96e4bd764a821c7ad946fe709.png) и
и  — число элементов
множества
— число элементов
множества 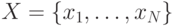 .
.Примером коэффициента размытости может служить логарифмическая энтропия нечетких множеств:

 — функция Шеннона
— функция Шеннона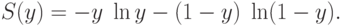
Выбор конкретного показателя зависит от условий задачи. Далее мы покажем,
что показатель
размытости нечетких множеств может быть задан с помощью метрики.
Необходимо обратить внимание на связь между показателем размытости
нечетких множеств и неопределенностью, возникающей при принятии решения, к
какому из
двух классов, "  " или "не
" или "не  "
, отнести объекты множества
"
, отнести объекты множества  .
На практике человеку часто приходится принимать подобные решения,
когда необходимо отнести объект к одному из двух классов, характеризующихся
противоположными свойствами типа: "белый—черный",
"пригоден—не пригоден",
"нравится—не нравится", "хороший—плохой" и т.п.
Такая альтернатива
вызывает у лица, принимающего решения, неопределенность,
обусловленную тем, что объекты часто обладают сразу обоими противоположными
свойствами, хотя и в разной мере. Можно предположить, что показатель
этой неопределенности зависит от размытости ситуации, в которой принимается
решение.
Допускается, что показатель неопределенности решений может удовлетворять
тем же свойствам, что и показатель размытости нечетких множеств.
.
На практике человеку часто приходится принимать подобные решения,
когда необходимо отнести объект к одному из двух классов, характеризующихся
противоположными свойствами типа: "белый—черный",
"пригоден—не пригоден",
"нравится—не нравится", "хороший—плохой" и т.п.
Такая альтернатива
вызывает у лица, принимающего решения, неопределенность,
обусловленную тем, что объекты часто обладают сразу обоими противоположными
свойствами, хотя и в разной мере. Можно предположить, что показатель
этой неопределенности зависит от размытости ситуации, в которой принимается
решение.
Допускается, что показатель неопределенности решений может удовлетворять
тем же свойствам, что и показатель размытости нечетких множеств.
