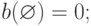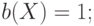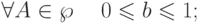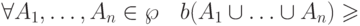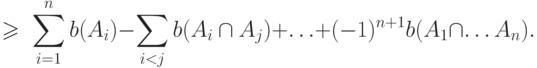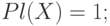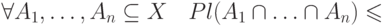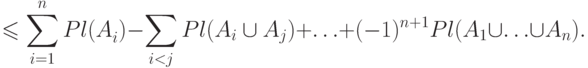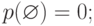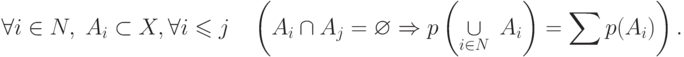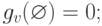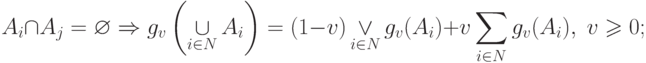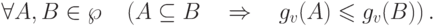|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Лекция 4: Показатель размытости нечетких множеств. Нечеткие меры и интегралы
Супераддитивные меры
Функция доверия. Определение функции доверия
предполагает,
что степень доверия высказыванию  , которое является истинным,
не обязательно равна 1. Это означает, что сумма степеней доверия
высказыванию
, которое является истинным,
не обязательно равна 1. Это означает, что сумма степеней доверия
высказыванию  и его отрицанию
и его отрицанию 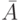 также не обязательно
равна 1, а может быть либо равной, либо меньшей 1. Другими словами,
когда высказывание
также не обязательно
равна 1, а может быть либо равной, либо меньшей 1. Другими словами,
когда высказывание  является истинным с определенной степенью
является истинным с определенной степенью ![s\in [0,1]](/sites/default/files/tex_cache/35a8edea94032c30d8fcc7bc7cc9c511.png) ,
его мера неопределенности выражается с помощью функции
,
его мера неопределенности выражается с помощью функции
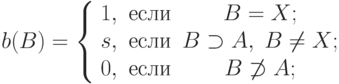
 .
.Если 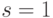 , то получаем меру, которая называется мерой
определенности, сосредоточенной на
, то получаем меру, которая называется мерой
определенности, сосредоточенной на  .
.
Если 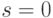 или
или 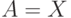 , то тогда
, то тогда 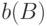 называется пустой функцией доверия
(полное незнание).
называется пустой функцией доверия
(полное незнание).
Итак, функция доверия — это мера, удовлетворяющая следующим свойствам:
Согласованная функция доверия. Понятие согласованной
функции доверия базируется на определении ядра 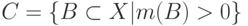 ,
полностью упорядоченного по вложению.
,
полностью упорядоченного по вложению.
Согласованная функция доверия определяется с помощью следующих аксиом:
Субаддитивные меры
Мера правдоподобия
Мера правдоподобия множества  из
из  определяется
как
определяется
как
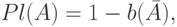
 — функция уверенности.
— функция уверенности.Мера правдоподобия удовлетворяет следующим аксиомам:
Пусть  и
и  - две меры - такие, что
- две меры - такие, что 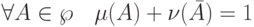 .
В этом случае
.
В этом случае  является функцией доверия тогда и только тогда,
если
является функцией доверия тогда и только тогда,
если  — мера правдоподобия.
— мера правдоподобия.
Мера возможности
Мерой возможности
называется функция ![\(\Pi :\wp \to [0,1]\)](/sites/default/files/tex_cache/504d8955b7d0fd2edcfdd80245c172c3.png) , удовлетворяющая следующим аксиомам:
, удовлетворяющая следующим аксиомам:
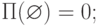
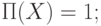
-

где
 — множество натуральных чисел.
— множество натуральных чисел.
Пусть  и
и  - две меры - такие, что
- две меры - такие, что 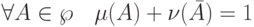 . Нечеткая
мера
. Нечеткая
мера  является согласованной функцией доверия тогда и только
тогда, если
является согласованной функцией доверия тогда и только
тогда, если  является мерой возможности.
является мерой возможности.
Мера вероятности
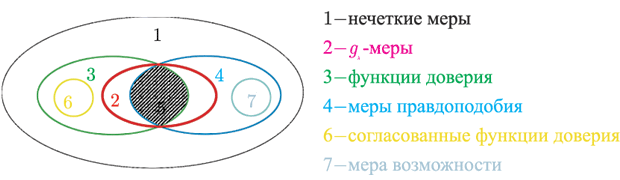
Вероятностная мера ( 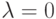 )
является частным случаем функции доверия или меры правдоподобия (см. рис. 4.1). Нечеткая мера
)
является частным случаем функции доверия или меры правдоподобия (см. рис. 4.1). Нечеткая мера  является вероятностной мерой тогда и только тогда,
если выполняются следующие условия:
является вероятностной мерой тогда и только тогда,
если выполняются следующие условия:
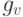 -мера
-мера
Нечеткая мера 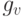 называется
называется 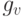 -мерой, если она удовлетворяет следующим аксиомам:
-мерой, если она удовлетворяет следующим аксиомам:
Очевидно, что при 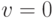 ,
, 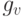 -мера является мерой
возможности, а при
-мера является мерой
возможности, а при 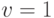 —
вероятностной мерой. Если
—
вероятностной мерой. Если  , то
, то 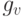 -мера
описывает неопределенность,
отличающуюся по своим свойствам от вероятности или возможности.
-мера
описывает неопределенность,
отличающуюся по своим свойствам от вероятности или возможности.