|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Нечеткие числа и операции над ними
Нечеткие числа (L-R)-типа — это разновидность нечетких чисел специального вида, т.е. задаваемых по определенным правилам с целью снижения объема вычислений при операциях над ними.
Функции принадлежности нечетких чисел
(L-R)-типа задаются с помощью
невозрастающих на множестве неотрицательных действительных чисел
функций действительного переменного 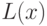 и
и 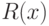 ,
удовлетворяющих свойствам:
,
удовлетворяющих свойствам:
а) 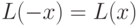 ,
, 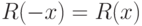 ;
;
б) 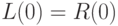 .
.
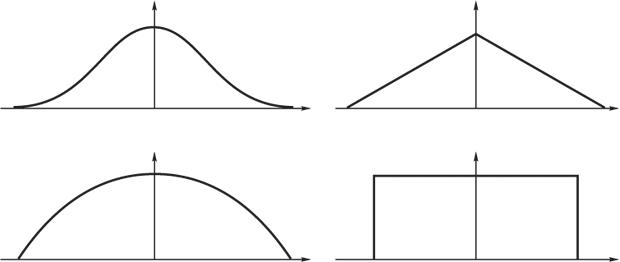
Очевидно, что к классу  -функций относятся функции,
графики которых
имеют следующий вид (см. рис. 7.1).
-функций относятся функции,
графики которых
имеют следующий вид (см. рис. 7.1).
Пусть 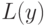 и
и 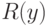 — функции
— функции  -типа. Унимодальное нечеткое
число
-типа. Унимодальное нечеткое
число  с модой
с модой  (т.е.
(т.е.  ) задается с помощью
) задается с помощью 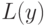 и
и 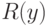 следующим образом:
следующим образом:
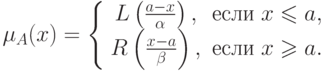
 — мода;
— мода; 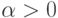 ,
,  — левый и правый коэффициенты нечеткости.
— левый и правый коэффициенты нечеткости.Таким образом, при заданных 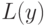 и
и 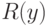 нечеткое число
(унимодальное)
задается тройкой
нечеткое число
(унимодальное)
задается тройкой 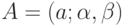 .
.
Толерантное нечеткое число задается, соответственно, четверкой
параметров 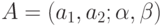 , где
, где 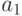 и
и 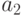 —
границы толерантности, т.е. в промежутке
—
границы толерантности, т.е. в промежутке ![[a_{1},a_{2}]](/sites/default/files/tex_cache/f540fa880e682ca99305a75d47ccb8ea.png) значение
функции принадлежности
равно
значение
функции принадлежности
равно  .
.
Примеры графиков функций принадлежности нечетких чисел  -типа приведены
на рис. 7.2.
-типа приведены
на рис. 7.2.
Толерантные нечеткие числа
(L-R)-типа называют трапезоидными числами.
Если мы оцениваем параметр качественно, например, говоря: "Это значение
параметра является средним ", необходимо ввести уточняющее
высказывание
типа " Среднее значение — это примерно
от  до
до  ", которое
есть предмет экспертной оценки (нечеткой классификации), и тогда можно
использовать
для моделирования нечетких классификаций трапезоидные числа.
На самом деле, это самый естественный способ неуверенной классификации.
", которое
есть предмет экспертной оценки (нечеткой классификации), и тогда можно
использовать
для моделирования нечетких классификаций трапезоидные числа.
На самом деле, это самый естественный способ неуверенной классификации.
Унимодальные нечеткие числа
(L-R)-типа называют треугольными числами. Треугольные
числа формализуют высказывания типа "приблизительно
равно  ". Ясно, что
". Ясно, что 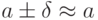 , причем по мере убывания
, причем по мере убывания  до нуля степень уверенности в оценке растет до единицы.
до нуля степень уверенности в оценке растет до единицы.
Нечеткие треугольные числа — это наиболее часто используемый тип нечетких чисел, причем чаще всего — в качестве прогнозных значений параметра.