|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Нечеткая логика
Операции конъюнкции и дизъюнкции
Как отмечалось на предыдущих лекциях, операции конъюнкции 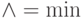 и
и 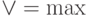 ,
введенные Заде, обладают почти всеми свойствами соответствующих
булевых операций. Это позволяет легко обобщать для нечеткого случая многие
понятия "четкой" логики. Однако с других точек зрения эти операции
являются
ограничительными. Возможность рассмотрения более "мягких" операций
конъюнкции и дизъюнкции обсуждал еще Заде в своих первых работах.
,
введенные Заде, обладают почти всеми свойствами соответствующих
булевых операций. Это позволяет легко обобщать для нечеткого случая многие
понятия "четкой" логики. Однако с других точек зрения эти операции
являются
ограничительными. Возможность рассмотрения более "мягких" операций
конъюнкции и дизъюнкции обсуждал еще Заде в своих первых работах.
Целесообразность применения тех или иных операций конъюнкции и дизъюнкции в нечеткой логике может рассматриваться с разных позиций в зависимости от области приложения нечеткой логики.
Во-первых, эти операции интересны с точки зрения моделирования
лингвистических
связок "и" и "или", используемых человеком. С одной
стороны, операции  и
и 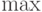 являются адекватными в порядковых шкалах, в которых обычно измеряются
лингвистические оценки. Это обусловливает их широкое применение в нечетких
лингвистических моделях. Однако, недостатком этих операций является то, что их
результат
равен значению одного операнда и не меняется при изменении значений второго
операнда в определенном диапазоне величин. Например,
являются адекватными в порядковых шкалах, в которых обычно измеряются
лингвистические оценки. Это обусловливает их широкое применение в нечетких
лингвистических моделях. Однако, недостатком этих операций является то, что их
результат
равен значению одного операнда и не меняется при изменении значений второго
операнда в определенном диапазоне величин. Например, 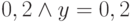 для всех
значений
для всех
значений 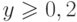 . Кроме того, в ряде экспериментальных работ
было установлено,
что операции
. Кроме того, в ряде экспериментальных работ
было установлено,
что операции  и
и 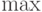 не являются достаточно
удовлетворительными с точки
зрения моделирования лингвистических связок. Это привело к появлению работ по
разработке
строго монотонных операций в порядковых шкалах, по настраиваемым на эксперта
табличным операциям, а также стимулировало исследования по поиску новых
операций
конъюнкции и дизъюнкции.
не являются достаточно
удовлетворительными с точки
зрения моделирования лингвистических связок. Это привело к появлению работ по
разработке
строго монотонных операций в порядковых шкалах, по настраиваемым на эксперта
табличным операциям, а также стимулировало исследования по поиску новых
операций
конъюнкции и дизъюнкции.
Во-вторых, расширение класса операций конъюнкции и дизъюнкции было вызвано
необходимостью построения достаточно общих математических моделей, которые
могли бы с единых позиций рассматривать, например, вероятностные и
многозначные
логики, различные методы принятия решений, обработки данных и т.д. Подобное
расширение произошло в результате введения в рассмотрение недистрибутивных
операций
конъюнкции и дизъюнкции, известных под названием  -норм и
-норм и  -конорм.
-конорм.
Докажем, что условие дистрибутивности совместно с условиями монотонности и
граничными
условиями однозначно определяет операции Заде. Итак, пусть нам даны две
операции  и
и  , удовлетворяющие следующим
условиям:
, удовлетворяющие следующим
условиям:
- Дистрибутивность:
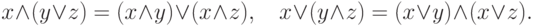
- Монотонность:
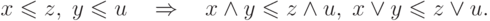
- Граничные условия:

Из монотонности и граничных условий следует выполнение условий:

Далее выводится условие идемпотентности дизъюнкции:
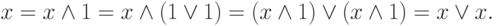
И из
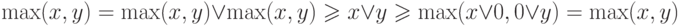

Аналогично выводится 
Установлено, что именно условие дистрибутивности является наиболее жестким
ограничением на возможную форму операций конъюнкции и дизъюнкции. Удаление
этого свойства из множества аксиом устраняет единственность операций  и
и 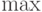 и дает
возможность совершать построения широкого спектра нечетких связок. Свойство
дистрибутивности очень важно в логике, так как оно дает возможность совершать
эквивалентные преобразования логических форм из дизъюнктивной в конъюнктивную
форму и обратно. Оно активно используется в процедурах минимизации логических
функций, в процедурах логического вывода на основе принципа резолюции и т.п.
Однако, во многих задачах такие преобразования логических форм не являются
необходимыми, и поэтому оказалось, что свойство дистрибутивности может быть
"довольно
безболезненно" удалено из системы аксиом, определяющих нечеткие операции
конъюнкции и дизъюнкции. Основной аксиомой для них является
ассоциативность, и свойства
этих операций во многом определяются общими свойствами ассоциативных функций и
операций,
активно изучающихся в математике.
и дает
возможность совершать построения широкого спектра нечетких связок. Свойство
дистрибутивности очень важно в логике, так как оно дает возможность совершать
эквивалентные преобразования логических форм из дизъюнктивной в конъюнктивную
форму и обратно. Оно активно используется в процедурах минимизации логических
функций, в процедурах логического вывода на основе принципа резолюции и т.п.
Однако, во многих задачах такие преобразования логических форм не являются
необходимыми, и поэтому оказалось, что свойство дистрибутивности может быть
"довольно
безболезненно" удалено из системы аксиом, определяющих нечеткие операции
конъюнкции и дизъюнкции. Основной аксиомой для них является
ассоциативность, и свойства
этих операций во многом определяются общими свойствами ассоциативных функций и
операций,
активно изучающихся в математике.
Простейшими примерами недистрибутивных операций являются следующие  -нормы и
-нормы и  -конормы:
-конормы:
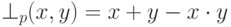 (вероятностная сумма),
(вероятностная сумма),
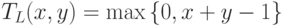 (t-норма
Лукасевича),
(t-норма
Лукасевича),
 (t-конорма
Лукасевича),
(t-конорма
Лукасевича),
![\( \bot _D (x,y) = \left\{ {\begin{array}{*{20}c}
{1,} & {\t{\char229}\t{\char241}\t{\char235}\t{\char232}\;(x,y) \in
(0,1] \times (0,1];} \\
{\max (x,y),} &
{\t{\char226}\;\t{\char239}\t{\char240}\t{\char238}\t{\char242}\t{\char232}\t{\char226}\t{\char237}\t{\char238}\t{\char236}\;\t{\char241}\t{\char235}\t{\char243}\t{\char247}\t{\char224}\t{\char229}.} \\
\end{array} } \right.
\)](/sites/default/files/tex_cache/2aa9e9a2a2b873f21d4582aac454f7c1.png) (сильная сумма).
(сильная сумма).
Для любых  -норм
-норм  и
и  -конорм
-конорм 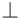 выполняются следующие
неравенства:
выполняются следующие
неравенства:
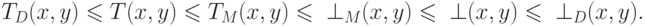
Таким образом,  -нормы
-нормы 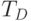 и
и 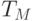 являются минимальной и максимальной
границами для всех
являются минимальной и максимальной
границами для всех  -норм. Аналогично,
-норм. Аналогично,  -конормы
-конормы  являются минимальной и максимальной границами для всех
являются минимальной и максимальной границами для всех  -конорм.
Эти неравенства очень важны для практического применения, так как они
устанавливают
границы возможного варьирования операций недистрибутивных конъюнкции и
дизъюнкции.
-конорм.
Эти неравенства очень важны для практического применения, так как они
устанавливают
границы возможного варьирования операций недистрибутивных конъюнкции и
дизъюнкции.
В-третьих, рассмотрение логических операций конъюнкции и дизъюнкции как
вещественных
функций, являющихся компонентами нечетких моделей процессов и систем,
естественно вызывает необходимость рассмотрения широкого класса таких функций,
увеличивающих гибкость моделирования. По этим причинам, в ряде приложений нечеткой
логики некоторые аксиомы  -норм и
-норм и  -конорм также оказались
ограничительными. В частности, параметрические классы данных операций имеют
достаточно сложный вид, затрудняющий их аппаратную реализацию и оптимизацию
нечетких
моделей по параметрам этих операций. Сложность параметрических классов
конъюнкций и дизъюнкций определяется способом генерации этих операций, который
фактически
определяется условием ассоциативности. С этой точки зрения свойство
ассоциативности
может рассматриваться как ограничительное. В то же время, свойство
коммутативности
операций конъюнкции и дизъюнкции может рассматриваться как необязательное
ограничение на эти операции, так как в общем случае в нечетких моделях операнды
данных операций могут характеризовать переменные, по-разному влияющие на
результат.
Свойства ассоциативности и коммутативности являются важными, например, в
нечетких
моделях многокритериального принятия решений, поскольку одним из разумных
требований,
накладываемых на процедуры принятия решений, является их независимость от
порядка
рассмотрения альтернатив и критериев. Но для систем нечеткого вывода эти
свойства
не всегда являются необходимыми, особенно когда позиции переменных в нечетких
правилах и процедуры обработки правил фиксированы, а также когда число входных
переменных не превышает двух, что бывает во многих реальных приложениях
нечетких
моделей. По этой причине из определения нечетких операций конъюнкции и дизъюнкции
могут быть удалены свойства коммутативности и ассоциативности так же, как это
было ранее сделано со свойствами дистрибутивности.
-конорм также оказались
ограничительными. В частности, параметрические классы данных операций имеют
достаточно сложный вид, затрудняющий их аппаратную реализацию и оптимизацию
нечетких
моделей по параметрам этих операций. Сложность параметрических классов
конъюнкций и дизъюнкций определяется способом генерации этих операций, который
фактически
определяется условием ассоциативности. С этой точки зрения свойство
ассоциативности
может рассматриваться как ограничительное. В то же время, свойство
коммутативности
операций конъюнкции и дизъюнкции может рассматриваться как необязательное
ограничение на эти операции, так как в общем случае в нечетких моделях операнды
данных операций могут характеризовать переменные, по-разному влияющие на
результат.
Свойства ассоциативности и коммутативности являются важными, например, в
нечетких
моделях многокритериального принятия решений, поскольку одним из разумных
требований,
накладываемых на процедуры принятия решений, является их независимость от
порядка
рассмотрения альтернатив и критериев. Но для систем нечеткого вывода эти
свойства
не всегда являются необходимыми, особенно когда позиции переменных в нечетких
правилах и процедуры обработки правил фиксированы, а также когда число входных
переменных не превышает двух, что бывает во многих реальных приложениях
нечетких
моделей. По этой причине из определения нечетких операций конъюнкции и дизъюнкции
могут быть удалены свойства коммутативности и ассоциативности так же, как это
было ранее сделано со свойствами дистрибутивности.
В качестве примера некоммутативных, неассоциативных операций дизъюнкции и конъюнкции можно привести следующие:
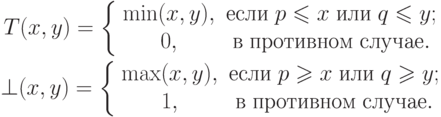

 (
(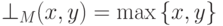 (
(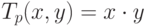 (
( (сильное
(сильное