НОУ ИНТУИТ | Основы теории нечетких множеств. Лекция 8: Нечеткая логика

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.07.2006 | Уровень: специалист | Доступ: свободно

Вам нравится? Нравится 36 студентам

| Поделиться |

Поддержать программу

Операции отрицания

Пусть множество значений функций принадлежности является линейно упорядоченным множеством с наименьшим 0 и наибольшим 1 элементами. Примером может служить интервал вещественных чисел [0,1] , шкала лингвистических оценок (например, L={"неправдоподобно", "малоправдоподобно", "средняя правдоподобность", "большая правдоподобность", "наверняка"}, шкала балльных оценок и др.

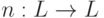Определение. Операцией отрицания на называется функция $n:L\to L$ , удовлетворяющая следующим условиям:

(О1) 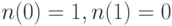n(0)=1, n(1)=0 ;

(O2) 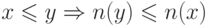$x \le y \Rightarrow n(y) \le n(x)$ .

В зависимости от выполнения на дополнительных условий, рассматриваются следующие типы отрицаний:

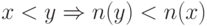Строгое отрицание: $x < y \Rightarrow n(y)< n(x)$ ;
Квазистрогое отрицание: $[x<y \& n(x)=n(y)] \Rightarrow n(x),n(y)\in \{0,1\}$ ;
Инволюция: ;
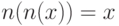Обычное отрицание: $n(n(x)) \le x$ ;
Слабое отрицание: $x \le n(n(x))$ .

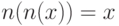Слабое отрицание называется также интуиционистским отрицанием. Элемент из будет называться иволютивным элементом, если n(n(x))=x , в противном случае он будет называться неиволютивным. Отрицание будет называться неиволютивным, если содержит неиволютивные по этому отрицанию элементы.

Элемент 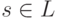$s\in L$ , удовлетворяющий условию 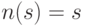n(s)=s , называется фиксированной точкой. Этот элемент будет центральным элементом (фокусом) . Очевидно, что если фиксированная точка существует, то она единственна.

Отрицание называется сжимающим в точке $x\in L$ , если выполнено условие

$x \wedge n(x) \le n(n(x)) \le x \vee n(x).$

Отрицание называется сжимающим на , если оно сжимающее в каждой точке множества .

Отрицание называется разжимающим в точке $x\in L$ , если выполнено условие

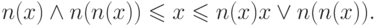
$n(x) \wedge n(n(x)) \le x \le n(x)x \vee n(n(x)).$

Отрицание называется разжимающим на , если оно является разжимающим в каждой точке множества .

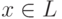Теорема Для любого отрицания любая точка $x\in L$ является либо сжимающей, либо разжимающей.

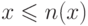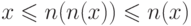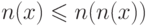Доказательство Пусть $x\le n(x)$ , тогда из условия (О2) получим $n(n(x))\le n(x)$ , откуда следует либо $x\le n(n(x))\le n(x)$ , либо $n(n(x))\le x\le n(x)$ . Аналогично, из $n(x)\le x$ получаем $n(x)\le n(n(x))$ , и, следовательно, либо 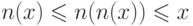$n(x)\le n(n(x))\le x$ , либо $n(x)\le x\le n(n(x))$

Следствие Элемент является иволютивным тогда и только тогда, если он одновременно сжимающий и разжимающий.

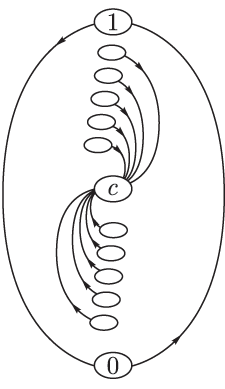
Используя математические методы, можно доказать, что элементы, порождаемые сжимающими и разжимающими отрицаниями в точках, представляют собой спирали, соответственно "закручиваемые внутрь" или "раскручиваемые наружу". Эти спирали либо бесконечные, либо в конечном случае имеют петлю на конце, состоящую из двух элементов, которые для сжимающих отрицаний могут совпадать, образуя неподвижную точку отрицания. Спирали, порождаемые разными элементами, либо вложены друг в друга, либо совпадают, начиная с некоторого элемента.

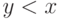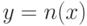На рис. 8.1 даны примеры сжимающего и разжимающего в точке отрицания. Элементы представлены вершинами соответствующего графа и упорядочены снизу вверх, в частности, y<x . Элементы y порождаются элементами так, что y=n(x) для рис. 8.1(А) и 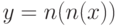y=n(n(x)) для рис. 8.1(Б).

Рис. 8.1.

Рассмотрим простейшие примеры отрицаний. Во всех примерах предполагается, что содержит элементы, отличные от 0 и 1.

Пример. "Все, что не истина и не ложь, является неопределенностью".

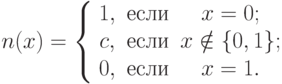
$n(x) = \left\{ {\begin{array}{*{20}c} {1,} & {\t{\char229}\t{\char241}\t{\char235}\t{\char232}} & {x = 0;} \\ {c,} & {\t{\char229}\t{\char241}\t{\char235}\t{\char232}} & {x \notin \{ 0,1\} ;} \\ {0,} & {\t{\char229}\t{\char241}\t{\char235}\t{\char232}} & {x = 1.} \\ \end{array} } \right.$