|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Нечеткие алгоритмы обучения
Обучение на основе условной нечеткой меры
Пусть 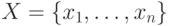 — множество причин (входов)
и
— множество причин (входов)
и  — множество результатов. Если
— множество результатов. Если  —
функция из
—
функция из  в интервал
в интервал ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) ,
, 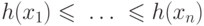 и
и 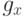 — нечеткая мера на
— нечеткая мера на  , то
, то
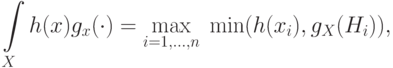
 .
.Задача состоит в оценке (уточнении) причин по нечеткой информации.
Пусть  — нечеткая мера на
— нечеткая мера на  ,
,  связана с
связана с 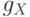 условной нечеткой
мерой
условной нечеткой
мерой  :
:

Предполагается следующая интерпретация вводимых мер: 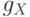 оценивает
степень нечеткости утверждения "один из элементов
оценивает
степень нечеткости утверждения "один из элементов  был
причиной",
был
причиной",  ,
, 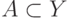 оценивает степень
нечеткости
утверждения "один из элементов
оценивает степень
нечеткости
утверждения "один из элементов  является результатом
благодаря
причине
является результатом
благодаря
причине  ";
"; 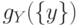 характеризует степень
нечеткости
утверждения: "
характеризует степень
нечеткости
утверждения: "  — действительный результат".
— действительный результат".
Пусть 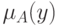 описывает точность информации
описывает точность информации  ,
тогда по определению
,
тогда по определению 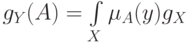 .
.
Метод обучения должен соответствовать обязательному условию: при получении
информации  нечеткая мера
нечеткая мера 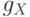 меняется таким
образом, чтобы
меняется таким
образом, чтобы  возрастала. Предположим, что
возрастала. Предположим, что  и
и  удовлетворяют
удовлетворяют  -правилу. Пусть
-правилу. Пусть 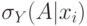 является убывающей, тогда
является убывающей, тогда
![g_Y (A) = \mathop \vee \limits_{i = 1}^n \left[ {\sigma _Y
(A|x_i ) \wedge g_X (F_i )} \right],](/sites/default/files/tex_cache/3695f8e93ab653c29e0ba04d53ef9a7a.png)
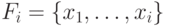 . При этих условиях существует
. При этих условиях существует  :
: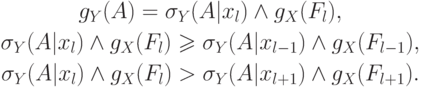
Обучение может быть осуществлено увеличением тех значений  (
( 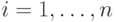 )
нечеткой меры
)
нечеткой меры 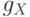 , которые увеличивают
, которые увеличивают  , и
уменьшением тех
значений
, и
уменьшением тех
значений  (
( 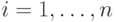 ) меры
) меры 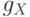 , которые
не увеличивают
, которые
не увеличивают  . Можно показать, что на величину
. Можно показать, что на величину  влияют
только такие
влияют
только такие  , что
, что 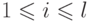 .
Следовательно, нечеткий
алгоритм обучения следующий:
.
Следовательно, нечеткий
алгоритм обучения следующий:

Параметр ![\alpha\in[0,1]](/sites/default/files/tex_cache/1e7d487c980f60db87f4890b9785d5ce.png) регулирует скорость обучения, т.е.
скорость
сходимости
регулирует скорость обучения, т.е.
скорость
сходимости 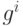 . Чем меньше
. Чем меньше  , тем сильнее
изменяется
, тем сильнее
изменяется 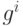 . В приведенном
алгоритме нет необходимости увеличивать
. В приведенном
алгоритме нет необходимости увеличивать 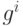 больше, чем на
больше, чем на 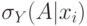 ,
так как большое увеличение
,
так как большое увеличение 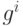 не влияет на
не влияет на  . Приведем некоторые
свойства модели обучения.
. Приведем некоторые
свойства модели обучения.
Свойство 1. Если повторно поступает одна и та же информация, то происходит следующее:
a. новое 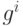 больше старого
больше старого 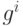 (
( 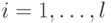 ) и новое
) и новое 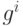 меньше старого
меньше старого 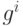 (
(  ),
следовательно, новая
мера
),
следовательно, новая
мера  не меньше старой меры
не меньше старой меры  , и
новая мера
, и
новая мера
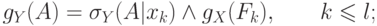
b. при предположении  ,
,  ,
, 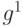 сходится к
сходится к  и
и 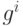 сходится к
0 для
сходится к
0 для  .
.
Свойство 2.
Если поступает одна и та же информация повторно:  для
всех
для
всех  ,
то
,
то 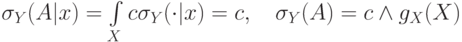 .
.
Следовательно, 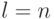 и
и 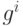 сходится к
сходится к  для всех
для всех  .
.
Свойство 3.
Предельное значение 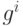 не зависит от начального значения тогда,
когда на вход повторно поступает одна и та же информация.
не зависит от начального значения тогда,
когда на вход повторно поступает одна и та же информация.
Пример. Рассмотрим модель глобального поиска экстремума неизвестной функции с несколькими локальными экстремумами. Для поиска глобального экстремума формируются критерии в виде некоторых функций:
 — оценивает число точек, проанализированных на предыдущих
шагах;
— оценивает число точек, проанализированных на предыдущих
шагах;
 — оценивает среднее значение функции по результатам
предыдущих шагов;
— оценивает среднее значение функции по результатам
предыдущих шагов;
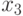 — оценивает число точек, значение функции в которых
принадлежит десятке лучших в своей области;
— оценивает число точек, значение функции в которых
принадлежит десятке лучших в своей области;
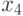 — оценивает максимум по прошлым попыткам;
— оценивает максимум по прошлым попыткам;
В описанном случае 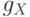 показывает степень важности
подмножеств
критериев и
показывает степень важности
подмножеств
критериев и  оценивает
предположение о нахождении
экстремума в блоке
оценивает
предположение о нахождении
экстремума в блоке 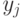 в соответствии с критерием
в соответствии с критерием  . Например,
. Например,  может зависеть от числа ранее проанализированных точек в блоке
может зависеть от числа ранее проанализированных точек в блоке 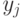 . Пусть
входная информация
. Пусть
входная информация  определяется формулой
определяется формулой

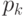 — максимум анализируемой функции, найденный к
рассматриваемому
моменту в блоке
— максимум анализируемой функции, найденный к
рассматриваемому
моменту в блоке 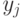 . Очевидно, что
. Очевидно, что  сходится к
максимизирующему множеству
функции. На каждой итерации осуществляется следующее: проверяется
заданное число новых точек; число этих точек выбирается пропорционально
сходится к
максимизирующему множеству
функции. На каждой итерации осуществляется следующее: проверяется
заданное число новых точек; число этих точек выбирается пропорционально  ;
в~каждой точке
;
в~каждой точке 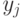 вычисляется и нормализуется мера
вычисляется и нормализуется мера 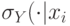 );
нормализуется
);
нормализуется 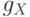 ; по
; по  и
и 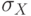 вычисляется
вычисляется  ,
а затем
,
а затем  ; посредством правил подкрепления корректируется
; посредством правил подкрепления корректируется  .
Затем выполняется новая итерация, и так до тех пор, пока не сойдется
.
Затем выполняется новая итерация, и так до тех пор, пока не сойдется  .
.
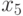 — оценивает
— оценивает