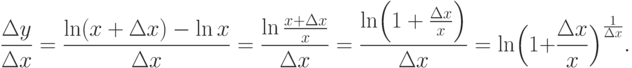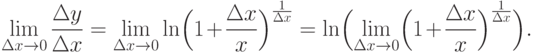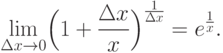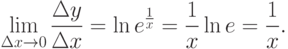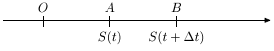НОУ ИНТУИТ | Введение в математику. Лекция 8: Дифференцирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 18.04.2007 | Уровень: для всех | Доступ: свободно | ВУЗ: Кабардино-Балкарский государственный университет

|

Вам нравится? Нравится 124 студентам

| Поделиться |

Поддержать программу

Аннотация: Рассматриваются основные математические понятия и теоремы, связанные с производной функции одной и многих переменных, а также их приложения.

Ключевые слова: функция, приращением аргумента, Приращением функции, ПО, прямой, путь, значение, предел, Касательной, Производной функции, приращение функции, приращение аргумента, определение, геометрический смысл производной в точке, график функции, механический смысл производной, уравнение касательной в точке, область определения, дифференцирование, производные, производная функции, натуральный логарифмы, замечательный предел, равенство, обратная функция, Дифференциалом, дифференциал, второй производной, вторая производная, третьей производной, минимум, максимум, в точке, окрестность, место, неравенство, точкой экстремума, экстремумом функции, экстремум, критической точкой, теорема Ферма, критическая точка, правило 1 нахождения экстремума функции, правило 2 нахождения экстремума функции, экстремум функции, график, Правило исследования монотонности дифференцируемой функции, Асимптотой, асимптота, четность, периодичность, частной производной, частная производная по, вычисление, частная производная, переменная, максимума, минимума, точками экстремума, критическими точками

Дифференцирование

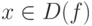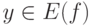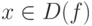Пусть задана функция y=f(x), $x\in D(f)$ , $y\in E(f)$ и точка $x_1=x+\Delta x\in D(f)$ , где $x\in D(f)$ . Тогда число 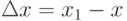$\Delta x=x_1-x$ называется приращением аргумента в точке x . Приращением функции 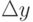$\Delta y$ в точке x соответствующего приращения 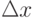$\Delta x$ называется число $\Delta y=y_1-y=f(x+\Delta x)-f(x)$ .

Рассмотрим несколько задач, которые привели к необходимости введения понятия производной функции.

Пример (Задача о движении). Некоторая точка движется по прямой по закону s=s(t), t - время (отсчитываемое от некоторой точки O ). Пусть в момент t=t₀ точка находилась в положении A, а при t=t₁ - в положении B (рис. 8.1).

Рис. 8.1. Прямолинейное движение точки

Тогда за время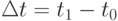 $\Delta t=t_1-t_0$ точка прошла путь $|\overrightarrow{AB}|=s(t+\Delta t) - s(t)=\Delta s$ . Средняя скорость за промежуток времени $\Delta t$ равна

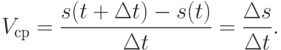
$V _{\text{ср}} = \frac {s(t+\Delta t)-s(t)}{\Delta t} = \frac {\Delta s}{\Delta t}.$

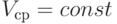Если движение равномерное, то $V_{\text{ср}}=const$ и этой характеристики достаточно для выяснения быстроты движения. Если же движение неравномерное, то $V_{\text{ср}}=V_{\text{ср}}(\Delta t)\ne const$ и поэтому вводится понятие мгновенной скорости прямолинейного движения (или скорость в данный момент времени

) как предельное значение средней скорости:

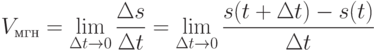
$V_{\text{мгн}} = \lim\limits_{\Delta t\to 0} \frac {\Delta s}{\Delta t} = \lim\limits_{\Delta t\to 0} \frac {s(t+\Delta t)-s(t)}{\Delta t}$

(если этот предел существует и он конечен). Ясно, что $V_{\text{мгн}} = V_{\text{мгн}}(t)$ .

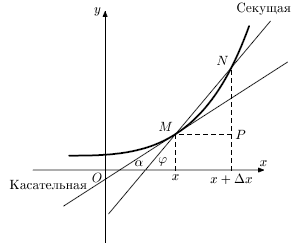
Пример (Задача о наклоне касательной к кривой). Пусть задана кривая y=f(x). Рассмотрим точки M(x; y) и 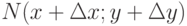$N(x+\Delta x; y+\Delta y)$ на этой кривой (рис. 8.2).

Рис. 8.2. Расположение касательной к секущей кривой

Касательной к линии y=f(x) в точке M называется прямая, которая совпадает с предельным значением прямой MN, когда точка N по кривой стремится к точке M, то есть 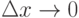$\Delta x\to 0$ . Так как $\tg \varphi = \frac {|\overrightarrow{NP}|}{|\overrightarrow{MP}|} = \frac {\Delta y}{\Delta x}$ , то $\tg\varphi \to \tg\alpha$ или угловой коэффициент k касательной к кривой можно определять как

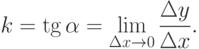
$k=\tg\alpha = \lim\limits_{\Delta x\to 0} \frac {\Delta y}{\Delta x}.$

Производной функции y=f(x) в точке x называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, при условии, что этот предел существует и конечен. Обозначают производную несколькими способами: y', f'(x), 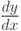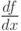$\frac {dy}{dx}$ , $\frac {df}{dx}$ . Таким образом,

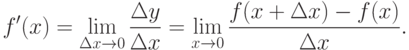
$f'(x)=\lim\limits_{\Delta x\to 0} \frac {\Delta y}{\Delta x} = \lim\limits_{x\to 0} \frac {f(x+\Delta x)-f(x)}{\Delta x}.$

Значение производной f'(x) при x=a (в точке x=a ) обозначается как:

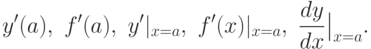
$y'(a), \ f'(a), \ y'|_{x=a},\ f'(x)|_{x=a} , \ \frac {dy}{dx} \bigl|_{x=a}.$

Пример. Вычислим y', где $y=\sqrt{x}$ при x=1, используя только определение производной.

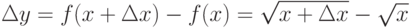Находим $\Delta y=f(x+\Delta x)-f(x)=\sqrt{x+\Delta x}-\sqrt{x}$ ;
Находим предел:
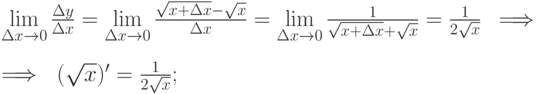
$\lim\limits_{\Delta x\to 0}\frac {\Delta y}{\Delta x} = \lim\limits_{\Delta x\to 0}\frac {\sqrt {x+\Delta x}-\sqrt{x}}{\Delta x} = \lim\limits_{\Delta x\to 0} \frac {1}{\sqrt{x+\Delta x}+\sqrt{x}} = \frac {1}{2\sqrt{x}} \ \implies \\ \implies \ (\sqrt{x})' = \frac {1}{2\sqrt{x}};$
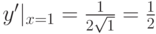Подставляя в это выражение x=1, находим $y'|_{x=1}=\frac {1}{2\sqrt{1}}=\frac 12$ .

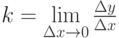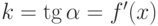В задаче о наклоне касательной мы выяснили, что угловой коэффициент касательной в точке x, проведенной к кривой y=f(x), будет иметь вид $k=\lim\limits_{\Delta x\to 0}\frac {\Delta y}{\Delta x}$ . Поэтому $k=\tg\alpha =f'(x)$ .

Отсюда следует геометрический смысл производной в точке x: значение производной равно тангенсу угла, который образован касательной к графику функции y=f(x), проведенной в точке M(x; f(x)), с положительным направлением оси Ox . В задаче о движении мы выяснили, что

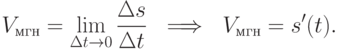
$V_{\text{мгн}}=\lim\limits_{\Delta t\to 0}\frac {\Delta s}{\Delta t} \ \implies \ V_{\text{мгн}} =s'(t).$

Отсюда следует механический смысл производной в точке x: значение производной равно мгновенной скорости (в момент времени x) материальной точки, движущейся по закону движения y=f(x) .

Найдем уравнение невертикальной касательной, проведенной к кривой y=f(x) в точке M₀(x₀;f(x₀)) (если касательная вертикальна, то f'(x) - не существует, так как при этом 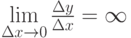$\lim\limits_{\Delta x\to 0}\frac {\Delta y}{\Delta x}=\infty$ ). Так как ее угловой коэффициент k=f'(x₀), то уравнение касательной в точке M₀ будет иметь вид: y-f(x₀)=f'(x₀)(x-x₀).

Если у функции y=f(x) существует производная в точке x, то говорят, что функция y=f(x) дифференцируема в точке x.

Теорема(необходимое условие существования производной). Если функция y=f(x) дифференцируема в некоторой точке 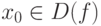$x_0\in D(f)$ , то она в этой точке непрерывна. Обратное утверждение неверно, то есть непрерывность функции в точке x не является достаточным условием ее дифференцируемости в этой точке, и функция может быть непрерывной в точке, не имея в этой точке производной.

Теорема(правила дифференцирования функций). Если функции u=f(x) и v=g(x) дифференцируемы в некоторой точке из общей части их областей определения, иначе говоря, в точке 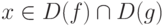$x\in D(f)\cap D(g)$ , то в этой точке дифференцируемы функции u+v, u-v, 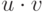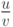$u\cdot v$ , $\frac uv$ , причем справедливы, соответственно, формулы (дифференцирования суммы, разности, произведения и частного):

$(u\pm v)'=u'\pm v'$ ,
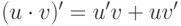$(u\cdot v)' =u'v+uv'$ ,
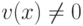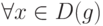$\Bigl(\frac uv\Bigr)' = \frac {u'v-v'u}{v^2}$ , $v(x)\ne 0$ , $\forall x\in D(g)$ .
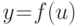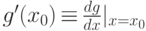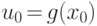Теорема(правило дифференцирования сложной функции). Пусть даны функции $\smu{1} y=f(u)$ , $\smu{1} u=g(x)$ , причем $\smu{1} E(g)\subset D(f)$ . Если существует в точке x₀ производная $\smu{3} g'(x_0)\equiv \frac {dg}{dx}|_{x=x_0}$ , а в точке $\smu{3} u_0=g(x_0)$ существует производная 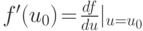$\smu{2} f'(u_0)=\frac {df}{du}|_{u=u_0}$ , то сложная функция 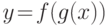$\smu{2} {y=f(g(x))}$ имеет производную в точке x₀, определяемую из формулы (дифференцирования сложной функции):
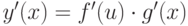
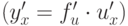$y'(x)=f'(u)\cdot g'(x)$ $(y'_x=f'_u\cdot u'_x)$ .

Найдем производные некоторых элементарных функций.

Теорема.

Производная постоянной равна нулю, то есть (C)'=0, C=const.
Производная функции y=sin x равна y'=cos x.
Производная функции y=cos x равна y'=-sin x.
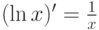Производная функции y=ln x равна $(\ln x)'=\frac 1x$ .
Имеет место формула (xⁿ)'= nx^n-1.
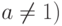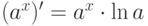Производная показательной функции при a>0, $a\ne 1)$ равна: $(a^x)'=a^x \cdot \ln a$ ,

Следствие. Для экспоненциальной функции (e^x)'=e^x.

Докажем, например, теорему для производной натурального логарифма.

Доказательство. Для всех 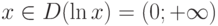$x\in D(\ln x)=(0;+\infty)$ имеем

$\frac {\Delta y}{\Delta x} = \frac {\ln (x+\Delta x)-\ln x}{\Delta x} = \frac {\ln \frac {x+\Delta x}{x}}{\Delta x} = \frac {\ln \Bigl(1+\frac {\Delta x}{x}\Bigr)}{\Delta x} = \ln \Bigl(1+\frac {\Delta x}{x} \Bigr)^{\frac {1}{\Delta x}}.$

Отсюда,

$\lim\limits_{\Delta x\to 0} \frac {\Delta y}{\Delta x} = \lim\limits_{\Delta x\to 0}\ln \Bigl(1+\frac {\Delta x}{x} \Bigr)^{\frac {1}{\Delta x}} = \ln \Bigl(\lim\limits_{\Delta x\to 0}\Bigl(1+\frac {\Delta x}{x} \Bigr)^{\frac {1}{\Delta x}} \Bigr).$