НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 6: Свойства линейного пространства

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3991 / 731 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции рассматриваются линейные пространства. Рассмотрены основные свойства линейных пространств, основные зависимости и возможные действия в них. Приведено также очень важное понятие базиса, доказаны основные теоремы и предоставлены задачи для самостоятельного решения

Ключевые слова: линейная комбинация, система элементов линейно независимая, линейное пространство над полем конечномерное, линейная выражаемость системы элементов, системы элементов эквивалентные

Линейные пространства

Вывод свойств линейного пространства из аксиом

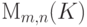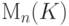Пусть K - поле (например, K= R - поле действительных чисел). Многочисленные конкретные примеры линейных пространств, с которыми мы уже столкнулись (линейные пространства строк Kⁿ, столбцов $\hat K^n$ , пространства прямоугольных и квадратных матриц $\mM_{m,n}(K)$ и $\mM_{n}(K)$ , пространство многочленов K[x], пространство непрерывных вещественных функций C[0,1] на отрезке [0,1] и т. д.), оправдывают введение и рассмотрение понятия линейного пространства _K V над полем K как множества V с операцией сложения ( 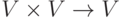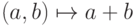$V\times V\to V$ , $(a,b)\mapsto a+b$ ) и операциями умножения на элементы 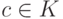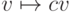$c\in K$ ( $V\to V$ , $v\mapsto cv$ ), удовлетворяющими следующим условиям:

I.1) ассоциативность сложения (т. е. (u+v)+w=u+(v+w) для всех 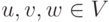$u,v,w\in V$ );

I.2) коммутативность сложения (т. е. u+v=v+u для всех 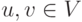$u,v\in V$ );

I.3) существование нейтрального элемента 0 для операции сложения (т. е. v+0=v для всех 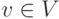$v\in V$ );

I.4) существование противоположного элемента -v для всякого 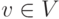$v\in V$ (т. е. v+(-v)=0 );

II.1) 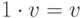$1\cdot v=v$ для всех $v\in V$ ;

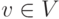II.2) (rs)v=r(sv) для всех 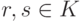$r,s\in K$ , $v\in V$ ;

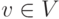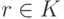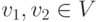III.1) r(v₁+v₂)=rv₁+rv₂ для всех $r\in K$ , $v_1,v_2\in V$ ;

III.2) (r+s)v=rv+sv для всех 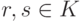$r,s\in K$ , $v\in V$ .

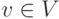Приведем вывод ряда следствий из этих аксиом линейного пространства (хотя, конечно, в каждом конкретном случае они достаточно очевидны).

Уравнение u+x=v для 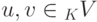$u,v\in {}_K V$ имеет, причем единственное, решение x=(-u)+v.

Действительно, прибавляя -u к левой и правой части, получаем, что x = (-u)+v. С другой стороны, u+(-u)+v=v.
Если x+x=x для 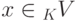$x\in {}_K V$ , то x=0.

Действительно, прибавляя к левой и правой части противоположный элемент -x, получаем, что x=(-x)+x+x=(-x)+x=0.
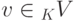0v=0 для любого $v\in {}_K V$ .

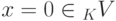Действительно, если x=0v (здесь $0\in K$ ), то x+x=0v+0v=(0+0)v=0v=x, и поэтому $x=0\in {}_K V$ .
r0=0 для $r\in K$ , $0\in V$ .

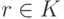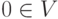Действительно, если x=r0, то x+x=r0+r0=r(0+0)=r0=x, и поэтому x=0.
(-1)v=-v для всех $v\in V$ .

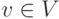Действительно, (-1)v+v=(-1+1)v=0v=0, т. е. (-1)v=-v.
rv=0 для 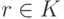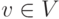$r\in K$ , $v\in V$ тогда и только тогда, когда либо r=0, либо v=0.

Действительно, если 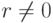$r\neq 0$ , то в поле K существует элемент 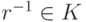$r^{-1}\in K$ , и поэтому v=1v=r^-1rv=r^-10=0.
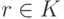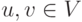r(u-v)=ru-rv для всех $r\in K$ , $u,v\in V$ .

Действительно, r(u-v)+rv=r(u-v+v)=ru, т. е. r(u-v)=ru-rv.
-(-v)=v для всех $v\in V$ .

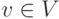Действительно, v+(-v)=0, и поэтому -(-v)=v.

Линейная зависимость в линейных пространствах

Пусть _K V - линейное пространство над полем K. Если 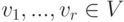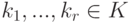$v_1,...,v_r\in V$ , $k_1,...,k_r\in K$ , то элемент

$k_1v_1+...+k_rv_r\in V$

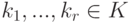называется линейной комбинацией элементов v₁,...,v_r с коэффициентами $k_1,...,k_r\in K$ .

Систему элементов 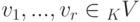$v_1,...,v_r \in {}_K V$ назовем линейно зависимой, если найдутся элементы 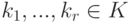$k_1,...,k_r\in K$ такие, что

а) не все k_i равны нулю (т. е. хотя бы один элемент k_i отличен от нуля);

б) k₁v₁+k₂v₂+...+k_rv_r=0.

Для краткости в этой ситуации мы будем говорить, что "нетривиальная" линейная комбинация элементов v₁,...,v_r равна нулю (конечно, тривиальная линейная комбинация всегда равна нулю, 0v₁+...+0 v_r=0 ).

Система элементов 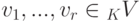$v_1,...,v_r\in {}_K V$ называется линейно независимой, если она не является линейно зависимой, это означает, что из равенства

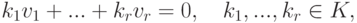
$k_1v_1+...+k_rv_r=0,\quad k_1,...,k_r\in K,$

следует, что k₁=k₂=...=k_r=0.

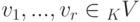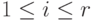Теорема 9.2.1. Система элементов $v_1,...,v_r \in {}_K V$ линейно зависима тогда и только тогда, когда для некоторого i, $1\le i\le r$ ,

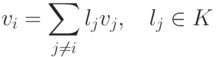
$v_i=\sum_{j\neq i}l_jv_j,\quad l_j\in K$

(т. е. элемент v_i является линейной комбинацией остальных элементов системы v₁,...,v_r ).

Доказательство.

Пусть система v₁,...,v_r линейно зависима, т. е.
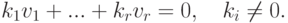
$k_1v_1+...+k_rv_r=0,\quad k_i\neq 0.$
Тогда
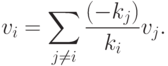
$v_i=\sum_{j\neq i}\frac{(-k_j)}{k_i}v_j.$
Если
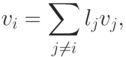$v_i=\sum_{j\neq i}l_jv_j,$
то
$\sum_{j\neq i} l_jv_j+(-1)v_i= v_i+(-1)v_i = 0,$
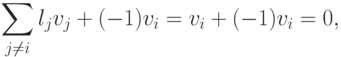
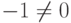т. е. система v₁,...,v_r линейно зависима, поскольку $-1\neq 0$ .

Пример 9.2.2. Если в системе элементов 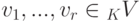$v_1,...,v_r\in {}_K V$ есть нулевой элемент, скажем, v_i=0, то система v₁...,v_r линейно зависима.

Действительно, 0 v₁+...+1 v_i+...+0 v_r=0, или, другим способом, 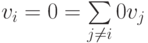$v_i=0=\sum\limits_{j\neq i}0 v_j$ .

Пример 9.2.3. Если v_i=v_j для 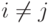$i\neq j$ , то система 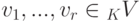$v_1,...,v_r\in {}_K V$ линейно зависима.

Действительно, 0 v₁+...+1 v_i+...+(-1) v_j+...+0 v_r=0, или, иначе, 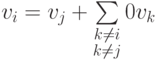$v_i=v_j+\sum\limits_{\substack{k\neq i\\ k\neq j}}0 v_k$ .

Пример 9.2.4. Система строк 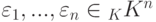$\varepsilon_1,...,\varepsilon_n\in {}_K K^n$ , где

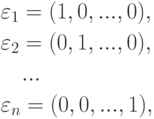
$\begin{align*} & \varepsilon_1=(1,0,...,0),\\ & \varepsilon_2=(0,1,...,0),\\ & \quad ...\\ & \varepsilon_n=(0,0,...,1), \end{align*}$

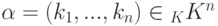линейно независима. Кроме того, любая строка $\alpha=(k_1,...,k_n)\in {}_K K^n$ является линейной комбинацией элементов 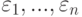$\varepsilon_1,...,\varepsilon_n$ , а именно, $\alpha=(k_1,...,k_n)=k_1\varepsilon_1+...+k_n\varepsilon_n$ .

Действительно,

$k_1\varepsilon_1+...+k_n\varepsilon_n=(k_1,...,k_n),$

и поэтому если

$k_1\varepsilon_1+...+k_n\varepsilon_n=(0,...,0),$

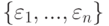то k₁=k₂=...=k_n=0, следовательно, система строк $\{\varepsilon_1,...,\varepsilon_n\}$ линейно независима.

Пример 9.2.5. Пусть 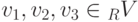$v_1,v_2,v_3\in {}_{ R} V$ - линейно независимая система в линейном пространстве _R V. Тогда u₁=v₁+v₂, u₂=v₁+v₃, u₃=v₂+v₃ - также линейно независимая система.

Действительно, если k₁ u₁ + k₂ u₂ + k₃ u₃ = 0, то

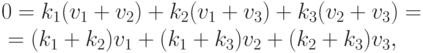
$\begin{mult} 0 = k_1 (v_1+v_2) + k_2 (v_1+v_3) + k_3 (v_2+v_3) ={} \\ {}=(k_1+k_2)v_1 + (k_1+k_3)v_2 + (k_2+k_3)v_3, \end{mult}$

поэтому

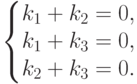
$\left\{ \begin{array}{@{}l@{}} k_1 + k_2 = 0,\\ k_1 + k_3 = 0,\\ k_2 + k_3 = 0. \end{array} \right.$

Следовательно, k₁ = 0, k₂ = 0, k₃ = 0, и система элементов u₁,u₂,u₃ линейно независима.

Упражнения 9.2.6.

Подсистема линейно независимой системы линейно независима.
Если подсистема линейно зависима, то линейно зависима и вся система.

Замечание 9.2.7. Для системы строк в Kⁿ

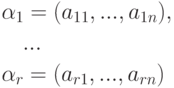
$\begin{align*} & \alpha_1 = (a_{11}, ..., a_{1n}),\\ & \quad ...\\ & \alpha_r = (a_{r1}, ..., a_{rn}) \end{align*}$

вопрос о ее линейной зависимости равносилен существованию ненулевого решения (k₁,...,k_r) следующей однородной системы линейных уравнений:

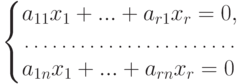
$\left\{ \begin{array}{@{}l@{}} a_{11} x_1 + ... + a_{r1} x_r = 0,\\ \dotfill\\ a_{1n} x_1 + ... + a_{rn} x_r = 0 \end{array} \right.$

с транспонированной матрицей A^*, где

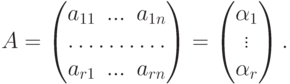
$A = \begin{pmatrix} a_{11} & ... & a_{1n}\\ \hdotsfor{3}\\ a_{r1} & ... & a_{rn} \end{pmatrix} = \begin{pmatrix} \alpha_1\\ \vdots\\ \alpha_r \end{pmatrix}.$

Таким образом, метод Гаусса дает нам в этом случае алгоритмическое решение задачи о линейной зависимости строк.

Теорема 9.2.8. Пусть $A=(a_{ij}) \in \mM_n(K)$ - квадратная матрица. Тогда следующие условия равносильны:

|A|=0 ;
система строк A₁, ..., A_n матрицы A линейно зависима (в пространстве строк Kⁿ );
система столбцов 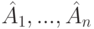$\hat A_1, ...,\hat A_n$ матрицы A линейно зависима (в пространстве столбцов $\hat K^n$ ).

Доказательство.

Если строки матрицы A линейно зависимы, скажем, i -я строка A_i является линейной комбинацией остальных, $A_i = \smash[b]{\sum\limits_{j \neq i} l_j A_j}$ , то, как мы показали, |A|=0, т. е. $2) \Longrightarrow 1)$ .
Пусть |A|=0. Тогда k₁ A₁ + ... + k_n A_n = 0 в том и только в том случае, если (k₁, ..., k_n) является решением однородной системы линейных уравнений с матрицей A^*. Так как |A^*| = |A| = 0, то существует ненулевое решение (k₁, ..., k_n), т. е. система строк A₁, ..., A_n матрицы A линейно зависима. Итак, $1) \Longrightarrow 2)$ .
Так как |A^*| = |A|, то $1) \iff 3)$ .

Задача 9.2.9. Пусть $A=(a_{ij})\in M_n(K)$ , $B=(b_{ij})\in M_n(K)$ , где b_ij=A_ji. Покажите, что если |A|=0, то |B|=0.

Теорема 9.2.10. Любая система из m строк в Kⁿ при m > n линейно зависима.

Доказательство. Если

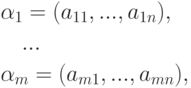
$\begin{align*} & \alpha_1 = (a_{11}, ..., a_{1n}),\\ & \quad ...\\ & \alpha_m = (a_{m1}, ..., a_{mn}), \end{align*}$

то равенство $k_1 \alpha_1 + ... + k_m \alpha_m = 0$ равносильно тому, что (k₁, ..., k_m) является решением следующей однородной системы линейных уравнений:

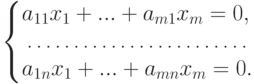
$\left\{ \begin{array}{@{}l@{}} a_{11} x_1 + ... + a_{m1} x_m = 0,\\ \dotfill\\ a_{1n} x_1 + ... + a_{mn} x_m = 0. \end{array} \right.$

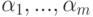Так как число n уравнений меньше числа m переменных, то однородная система обладает ненулевым решением, т. е. система $\alpha_1, ..., \alpha_m$ линейно зависима.

Следствие 9.2.11. Если система 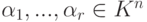$\alpha_1, ..., \alpha_r \in K^n$ линейно независима, то $r \leq n$ .

Лемма 9.2.12. Если система элементов 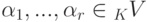$\alpha_1,...,\alpha_r\in {}_K V$ линейного пространства _K V над полем K линейно независима, 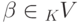$\beta \in {}_K V$ и система 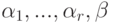$\alpha_1, ..., \alpha_r, \beta$ линейно зависима, то 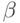$\beta$ является линейной комбинацией элементов $\alpha_1,...,\alpha_r$ .

Доказательство. Пусть

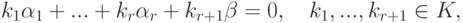
$k_1 \alpha_1 + ... + k_r \alpha_r + k_{r+1} \beta = 0, \quad k_1,...,k_{r+1}\in K,$

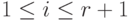где не все k_i, $1 \leq i \leq r+1$ , равны нулю. Если бы k_r+1=0, то нетривиальная линейная комбинация $k_1 \alpha_1 + ... + k_r \alpha_r = 0$ , равная нулю, означала бы, что система $\alpha_1, ..., \alpha_r$ линейно зависима, что противоречит предположению.

Итак, 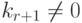$k_{r+1} \neq 0$ , и поэтому

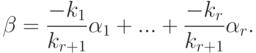
$\beta = \frac{-k_1}{k_{r+1}} \alpha_1 + ... + \frac{-k_r}{k_{r+1}} \alpha_r.$

Лемма 9.2.13 (единственность представления элемента линейного пространства KV в виде линейной комбинации линейно независимой системы элементов). Пусть 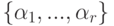$\{\alpha_1,...,\alpha_r\}$ - линейно независимая система элементов линейного пространства _K V и

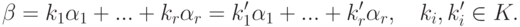
$\beta=k_1\alpha_1+...+k_r\alpha_r=k'_1\alpha_1+...+k'_r\alpha_r,\quad k_i,k'_i\in K.$

Тогда k₁=k'₁,...,k_r=k'_r.

Доказательство. Действительно,

$(k_1-k'_1)\alpha_1+...+(k_r-k'_r)\alpha_r= 0,$

и поэтому k₁ - k'₁=0,...,k_r - k'_r=0.

Дальше >>

Авторизоваться

Алгебра матриц и линейные пространства

Свойства линейного пространства

Линейные пространства

Вывод свойств линейного пространства из аксиом

Линейная зависимость в линейных пространствах

Вопросы и ответы