НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 6: Свойства линейного пространства

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3991 / 731 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Максимальные линейно независимые подсистемы систем элементов линейных пространств, базис линейного пространства

Пусть 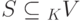$S\subseteq {}_K V$ . Наиболее важные для нас случаи:

а) S - конечное подмножество элементов в _K V ;

б) S = _K V.

Подсистема 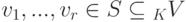$v_1,...,v_r \in S \subseteq {}_K V$ называется максимальной линейно независимой подсистемой в S, если:

1) v₁,...,v_r - линейно независимая система;

2) v₁,...,v_r,v - линейно зависимая система для всякого 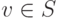$v \in S$ , или, что эквивалентно,

2') любой элемент 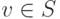$v \in S$ является линейной комбинацией элементов v₁,...,v_r.

Максимальная линейно независимая подсистема v₁,...,v_r в S = _KV (если в _K V существует такая конечная система) называется базисом линейного пространства _K V. Линейное пространство _K V с конечным базисом v₁,...,v_r называется конечномерным линейным пространством (при этом будет показано, что любой другой базис линейного пространства содержит то же самое число элементов).

Пример 9.3.1. Как мы уже видели, система строк

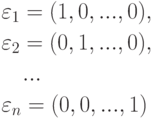
$\begin{align*} & \varepsilon_1 = (1,0,...,0),\\ & \varepsilon_2 = (0,1,...,0),\\ & \quad ... \\ & \varepsilon_n = (0,0,...,1) \end{align*}$

является базисом линейного пространства строк Kⁿ.

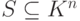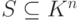Лемма 9.3.2. Любую линейно независимую подсистему v₁,...,v_r в $S \subseteq K^n$ можно дополнить до максимальной линейно независимой подсистемы в $S \subseteq K^n$ .

Доказательство. Если v₁,...,v_r - максимальная линейно независимая подсистема в 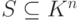$S \subseteq K^n$ , то все доказано. Если нет, то найдется элемент 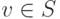$v \in S$ такой, что v₁,v₂,...,v_r,v=v_r+1 - линейно независимая подсистема в S. После конечного числа шагов процесс остановится, так как любые системы из n+1 элементов в линейном пространстве Kⁿ оказываются линейно зависимыми.

Следствие 9.3.3. Любой ненулевой элемент 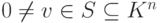$0 \neq v \in S \subseteq K^n$ дополняем до максимальной линейно независимой подсистемы в S.

Следствие 9.3.4. В S= Rⁿ (или S=Kⁿ для бесконечного поля K ) бесконечно много различных базисов. Если поле K конечно, |K|=q (например, K= Z₂ ), то число элементов в Kⁿ равно qⁿ, и поэтому число базисов в Kⁿ конечно. Найдите их число.

Замечание 9.3.5. Пусть строки 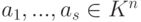$a_1,...,a_s\in K^n$ линейно независимы, s<n. Тогда существуют такие строки 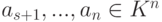$a_{s+1},...,a_n\in K^n$ , что {a₁,...,a_n} - базис линейного пространства Kⁿ. Практическое нахождение строк a_s+1,...,a_n можно осуществить следующим образом. 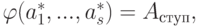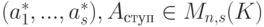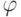Запишем строки a₁,...,a_s по столбцам и приведем полученную матрицу к ступенчатому виду: $\varphi(a_1^*,...,a_s^*)=A_{\textup{ступ}}, % \varphi(a_1^*,...,a_s^*)=A_{\textup{ступ}}$ , где $(a_1^*,...,a_s^*),A_{\textup{ступ}}\in M_{n,s}(K)$ , $\varphi$ - последовательность элементарных преобразований строк. Так как строки a₁,...,a_s линейно независимы, то в $A_{\textup{ступ}}$ имеется ровно s ненулевых строк (первые s строк). 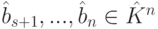Пусть $\hat b_{s+1},...,\hat b_n\in \hat K^n$ - столбцы, на i -м месте которых стоит 1, а остальные элементы равны 0, i=s+1,...,n. Припишем эти столбцы справа к матрице $A_{\textup{ступ}}$ . 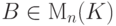Пусть $B\in \mM_n(K)$ - полученная матрица. 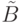Применяя к матрице B последовательность элементарных преобразований строк, обратную к $\varphi$ , приходим к матрице $\tilde B$ . При этом $(\tilde B)^*$ - матрица, в которой первые s строк - это a₁,...,a_s, а последующие строки дополняют их до базиса линейного пространства Kⁿ.