НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 10: Собственные числа и собственные векторы матрицы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3991 / 731 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции рассматриваются понятия собственных чисел и собственных векторов матрицы. Приведены основные определения, доказаны основные теоремы. Также приведены примеры решения задач и предоставлены задачи для самостоятельного решения

Ключевые слова: поле, матрица, переменная, многочлен, собственный вектор, вектор, размерность, собственное число, свободная переменная, доказательство, ПО, основание, TE

Собственные числа и собственные векторы матрицы

Пусть K - поле, 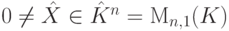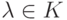$A\in M_{n}(K)$ , $0\neq \hat X\in\hat K^n=\mM_{n,1}(K)$ , $\lambda\in K$ . Если $A\cdot \hat X=\lambda\cdot \hat X$ , то $\lambda$ называется собственным числом матрицы A, а $\hat X$ - собственным вектором матрицы A, отвечающим собственному числу $\lambda$ .

Условие $A\cdot\hat X=\lambda\cdot \hat X$ эквивалентно условию

$(A-\lambda E)\hat X = \begin{pmatrix} 0\\ \vdots\\ 0 \end{pmatrix} \in \hat K^n,$

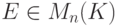где $E\in M_{n}(K)$ - единичная матрица. При фиксированном $\lambda$ это условие превращается в однородную систему линейных уравнений относительно неизвестных x₁,...,x_n,

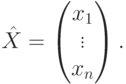
$\hat X= \begin{pmatrix} x_1\\ \vdots\\ x_n \end{pmatrix}.$

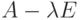Матрица $A-\lambda E$ этой системы - квадратная матрица размера n. Поэтому наличие ненулевого решения этой системы равносильно тому, что $|A-\lambda E|=0$ . Пусть t - переменная,

$p(t)=|A-tE|=p_nt^n+p_{n-1}t^{n-1}+...+p_0\in K[t]\text{ -}$

многочлен степени n от переменной t (называемый характеристическим многочленом матрицы A ), при этом:

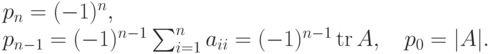
$\begin{gathe} p_n=(-1)^n,\\ p_{n-1}=(-1)^{n-1}\sum_{i=1}^{n}a_{ii}=(-1)^{n-1}\tr A,\quad p_0=|A|. \end{gathe}$

Мы показали, что собственные числа и только они являются корнями характеристического многочлена из поля K.

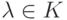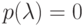Если $\lambda\in K$ и $p(\lambda)=0$ , то все собственные векторы матрицы A относительно собственного числа $\lambda$ - это все ненулевые решения системы

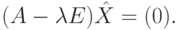
$(A-\lambda E)\hat X=(0)\in\hat K^n.$

Отметим, что множество всех собственных векторов матрицы A относительно собственного числа $\lambda$ не образует линейного подпространства в $\hat K^n$ , так как все эти векторы ненулевые. Но если к этому множеству добавить нулевой вектор, то получится линейное подпространство всех решений системы

$(A-\lambda E)\hat X=(0).$

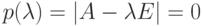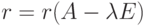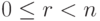Таким образом, если $p(\lambda)=|A-\lambda E|=0$ , $r=r(A-\lambda E)$ , то $0 \leq r < n$ , то размерность пространства решений этой системы равна s=n-r, поэтому 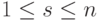$1 \leq s \leq n$ . 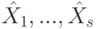Если {X₁,...,X_s} - какая\df либо фундаментальная система решений системы $(A-\lambda E)\hat X=(0)$ , то все собственные векторы матрицы A, отвечающие собственному числу $\lambda$ , - это все нетривиальные линейные комбинации элементов $\hat X_1,...,\hat X_s$ с коэффициентами из поля K.

Пример 9.19.1.

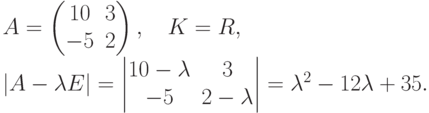
$\begin{gathe} A = \begin{pmatrix} \phm 10 & 3\\ -5 & 2 \end{pmatrix},\quad K= R,\\ |A-\lambda E| = \begin{vmatrix} 10-\lambda & 3\\ -5 & 2-\lambda \end{vmatrix} = \lambda^2-12\lambda+35. \end{gathe}$

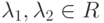Корни: $\lambda_1=7$ , $\lambda_2=5$ , $\lambda_1,\lambda_2\in R$ (собственные числа матрицы A ).

Собственные векторы для $\lambda_1=7 :$

$A-7E = \begin{pmatrix} \phm 3 & \phm 3\\ -5 & -5 \end{pmatrix},\quad \begin{pmatrix} \phm 3 & \phm 3\\ -5 & -5 \end{pmatrix} \begin{pmatrix} x_1\\ x_2 \end{pmatrix} = \begin{pmatrix} 0\\ 0 \end{pmatrix},$

ненулевые решения:

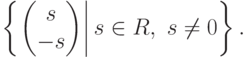
$\left\{\left.\begin{pmatrix}\phm s\\-s\end{pmatrix}\right| s\in R,\ s\neq 0\right\}.$

Собственные векторы для $\lambda_2=5 :$

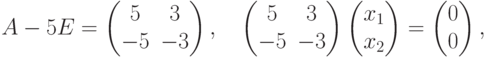
$A-5E = \begin{pmatrix} \phm 5 & \phm 3\\ -5 & -3 \end{pmatrix},\quad \begin{pmatrix} \phm 5 & \phm 3\\ -5 & -3 \end{pmatrix} \begin{pmatrix} x_1\\ x_2 \end{pmatrix} = \begin{pmatrix} 0\\ 0 \end{pmatrix},$

ненулевые решения:

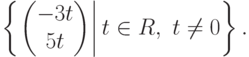
$\left\{\left.\begin{pmatrix}-3t\\\phm 5t\end{pmatrix}\right| t\in R,\ t\neq 0\right\}.$

Пример 9.19.2.

$\begin{gathe} K= C,\quad A=\begin{pmatrix} 0 & 1 & 0\\ 0 & 0 & 2\\ 0 & 0 & 0 \end{pmatrix},\\ p(\lambda)=|A-\lambda E|= \begin{vmatrix} -\lambda & \phm 1 & \phm 0\\ \phm 0 & -\lambda & \phm 2\\ \phm 0 & \phm 0 & -\lambda \end{vmatrix} = -\lambda^3. \end{gathe}$

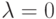Имеется лишь одно собственное число: $\lambda=0$ . Собственные векторы относительно $\lambda=0$ задаются системой линейных уравнений

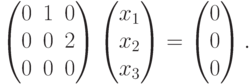
$\begin{pmatrix} 0 & 1 & 0\\ 0 & 0 & 2\\ 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix}.$

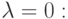
Система уже имеет ступенчатый вид, x₂, x₃ - главные неизвестные, x₁ - свободная переменная, множество собственных векторов относительно $\lambda=0 :$

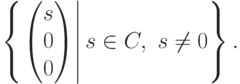
$\left\{\left. \begin{pmatrix} s\\ 0\\ 0 \end{pmatrix}\right| s\in C,\ s\neq 0\right\}.$

Пример 9.19.3. Если

$A= \begin{pmatrix} \alpha_1 & & \lefteqn{\raisebox{-5pt}[0pt][0pt]{\text{\hspace*{-10pt}\Large 0 }}}\\ & \ddots\\ \lefteqn{\raisebox{0pt}[0pt][0pt]{\text{\hspace*{0pt}\Large 0 }}} & & \alpha_n \end{pmatrix} \text{ -}$

диагональная матрица, то $\alpha_1,...,\alpha_n$ - все корни характеристического многочлена матрицы A (и следовательно, собственные числа).

Дальше >>

Авторизоваться

Алгебра матриц и линейные пространства

Собственные числа и собственные векторы матрицы

Собственные числа и собственные векторы матрицы

Вопросы и ответы