НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 2: Вычисление определителей

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3991 / 731 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В данной лекции рассматриваются примеры вычисления определителей. Приведены определения минора, алгебраического дополнения и определителя Вандермонда. Рассмотрены примеры решения задач и приведены упражнения для самостоятельного решения

Ключевые слова: определение, определитель, матрица, доказательство, функция, алгебраическое дополнение элемента матрицы, Алгебраическим дополнением, ПО, определитель матрицы, система линейных уравнений, коэффициенты

Вычисление определителей

Определение определителя

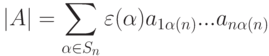
$|A|=\sum_{\alpha\in S_n} \varepsilon(\alpha) a_{1\alpha(n)}... a_{n\alpha(n)}$

как суммы n! слагаемых-произведений плохо пригодно для реальных вычислений при больших n. В теоретическом плане важно отметить, что определитель |A| является многочленом от n² переменных a_ij, в котором мономы входят с коэффициентами $\pm 1$ . Отметим лишь одно из следствий этого факта: если a_ij=a_ij(x) являются дифференцируемыми функциями от переменной x, то определитель |A| также является дифференцируемой функцией от x, поскольку суммы и произведения дифференцируемых функций являются дифференцируемыми функциями.

Теорема 6.6.1. Пусть от квадратной $(n\times n)$ -матрицы A=(a_ij) элементарными преобразованиями 1-го и 2-го типа ( t преобразований 2-го типа) мы пришли к треугольной матрице

$\bar A = \begin{pmatrix} \bar a_{11} & & & \raisebox{-10pt}[0pt][0pt]{\text{\hspace*{-25pt}\LARGE*}}\\ 0 & \bar a_{22}\\ \vdots & & \ddots\\ 0 & \hdotsfor{2} & \bar a_{nn} \end{pmatrix}$

(все элементы ниже диагонали равны нулю; любая ступенчатая матрица, очевидно, является треугольной). Тогда

$|A| = (-1)^t \bar a_{11}... \bar a_{nn}.$

Доказательство. Так как |A|= (-1)^t |A|, то

$|A|=(-1)^t |\bar A|= (-1)^t \bar a_{11}... \bar a_{nn}.$

Характеризация функции определителя матрицы базовыми свойствами

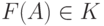Теорема 6.7.1 (о единственности функции с базовыми свойствами 1—4 определителя). Пусть функция F, сопоставляющая каждой квадратной $(n\times n)$ -матрице $A\in\mM_n(K)$ "число" $F(A)\in K$ , удовлетворяет базовым свойствам {1 4} функции определителя. Тогда F(A)=|A|, т. е. функция определителя |A| однозначно определяется свойствами {1 4}.

Доказательство. Приведем $(n\times n)$ -матрицу A к треугольному виду

$\bar A = \begin{pmatrix} \bar a_{11} & & & \raisebox{-10pt}[0pt][0pt]{\text{\hspace*{-25pt}\LARGE * }}\\ 0 & \bar a_{22}\\ \vdots & & \ddots\\ 0 & \hdotsfor{2} & \bar a_{nn} \end{pmatrix}$

элементарными преобразованиями строк 1-го и 2-го типа ( t преобразований 2-го типа). Тогда

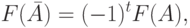
$F(\bar A)=(-1)^t F(A),$

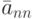следовательно, F(A)=(-1)^t F(A). Далее, вынося элемент $\bar a_{nn}$ из n -й строки и создавая 0 над ним, получаем

$%\begin{mult} \addtolength{\arraycolsep}{-2pt} F(\bar A) = \bar a_{nn} F \begin{pmatrix} \bar a_{11} & & & \raisebox{-10pt}[0pt][0pt]{\text{\hspace*{-45pt}\LARGE * }}\\ \vdots & \ddots\\ 0 & ... & \bar a_{n-1\,n-1}\\ 0 & ... & 0 & 1 \end{pmatrix} = %{} %\\ %{}= \bar a_{nn} F \begin{pmatrix} \bar a_{11} & & & 0\\ \vdots & \ddots & \raisebox{10pt}[0pt][0pt]{\text{\hspace*{-0pt}\LARGE * }} & \vdots\\ 0 & ... & \bar a_{n-1\,n-1} & 0\\ 0 & ... & 0 & 1 \end{pmatrix}. %\end{mult}$

Продолжая это рассуждение, получаем

$F(\bar A) = \bar a_{11}... \bar a_{nn} F \begin{pmatrix} 1 & & \lefteqn{\raisebox{-5pt}[0pt][0pt]{\text{\hspace*{-10pt}\Large 0 }}}\\ & \ddots\\ \lefteqn{\raisebox{0pt}[0pt][0pt]{\text{\hspace*{0pt}\Large 0 }}} & & 1 \end{pmatrix} = \bar a_{11} ... \bar a_{nn}.$

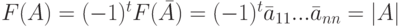Итак, $F(A)=(-1)^t F(\bar A) = (-1)^t \bar a_{11}... \bar a_{nn} = |A|$ .

Дальше >>

Авторизоваться

Алгебра матриц и линейные пространства

Вычисление определителей

Вычисление определителей

Характеризация функции определителя матрицы базовыми свойствами

Вопросы и ответы