Свойства линейного пространства
Замечание о линейной выражаемости конечных систем элементов в линейном пространстве
Пусть K V - линейное пространство, 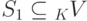 ,
, 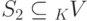 . Будем говорить, что система S2 элементов u1,...,us линейно выражается через систему S1 элементов v1,...,vr, если каждый элемент
. Будем говорить, что система S2 элементов u1,...,us линейно выражается через систему S1 элементов v1,...,vr, если каждый элемент 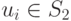 ,
, 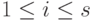 , является линейной комбинацией элементов v1,...,vr системы S1,
, является линейной комбинацией элементов v1,...,vr системы S1,

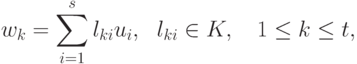

Системы S1 и S2 называются эквивалентными, если они линейно выражаются друг через друга (обозначение: 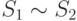 ).
).
Следствие 9.4.1. Отношение "быть эквивалентными системами", 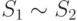 , является отношением эквивалентности.
, является отношением эквивалентности.
Следствие 9.4.2. Если элемент 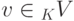 является линейной комбинацией элементов v1,...,vr системы S1,
является линейной комбинацией элементов v1,...,vr системы S1, 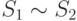 , где S2 - система элементов u1,...,us, то элемент v является линейной комбинацией элементов u1,...,us системы S2.
, где S2 - система элементов u1,...,us, то элемент v является линейной комбинацией элементов u1,...,us системы S2.
Следствие 9.4.3. Любая (конечная) система элементов  эквивалентна своей максимальной линейно независимой подсистеме.
эквивалентна своей максимальной линейно независимой подсистеме.
Следствие 9.4.4. Любые две (конечные) максимально независимые подсистемы любой системы  эквивалентны.
эквивалентны.
Замечание 9.4.5. Если 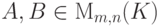 и матрица B получена из матрицы A конечным числом элементарных преобразований 1-го, 2-го и 3-го типов, то каждая строка матрицы B является линейной комбинацией строк матрицы A (поскольку от матрицы B мы можем вернуться к матрице A с помощью элементарных преобразований строк 1-го, 2-го и 3-го типов, то каждая строка матрицы A является линейной комбинацией строк матрицы B ). Таким образом, в линейном пространстве строк Kn системы строк A1,...,Am матрицы A и B1,...,Bm матрицы B линейно выражаются друг через друга.
и матрица B получена из матрицы A конечным числом элементарных преобразований 1-го, 2-го и 3-го типов, то каждая строка матрицы B является линейной комбинацией строк матрицы A (поскольку от матрицы B мы можем вернуться к матрице A с помощью элементарных преобразований строк 1-го, 2-го и 3-го типов, то каждая строка матрицы A является линейной комбинацией строк матрицы B ). Таким образом, в линейном пространстве строк Kn системы строк A1,...,Am матрицы A и B1,...,Bm матрицы B линейно выражаются друг через друга.
Теорема 9.4.6 (основная теорема о линейной зависимости). Пусть в линейном пространстве K V линейно независимая система элементов v1,...,vr линейно выражается через другую систему элементов u1,...,us. Тогда 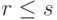 .
.
Доказательство. Допустим противное: пусть r > s. В силу нашего предположения
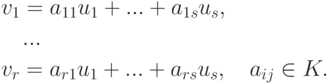
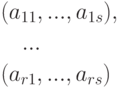
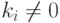 для некоторого i, равная нулевой строке
для некоторого i, равная нулевой строке  . Но тогда и линейная комбинация элементов v1, ..., vr с этими же коэффициентами k1, ..., kr, равна нулю, k1v1+...+krvr=0. Таким образом, система элементов v1,...,vr линейно зависима, что приводит нас к противоречию.
. Но тогда и линейная комбинация элементов v1, ..., vr с этими же коэффициентами k1, ..., kr, равна нулю, k1v1+...+krvr=0. Таким образом, система элементов v1,...,vr линейно зависима, что приводит нас к противоречию.Следствие 9.4.7. Две эквивалентные конечные линейно независимые системы в линейном пространстве K V содержат равное число элементов.
Следствие 9.4.8.Для системы 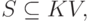 где KV —конечномерное линейное пространство, любые две (конечные) максимальные линейно независимые подсистемы содержат одинаковое число элементов r(S), называемое рангом системы S.
где KV —конечномерное линейное пространство, любые две (конечные) максимальные линейно независимые подсистемы содержат одинаковое число элементов r(S), называемое рангом системы S.
Следствие 9.4.9. Если S = K V и K V - конечномерное линейное пространство, то любые два базиса в K V состоят из одного и того же числа элементов n, это число n называется размерностью линейного пространства K V, обозначение: 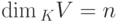 .
.
Как мы видели ранее, одним из базисов в линейном пространстве строк K Kn является система строк
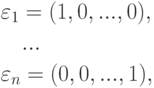
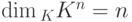 .
.Следствие 9.4.10. Если в конечномерном линейном пространстве K V одна система элементов S1 линейно выражается через другую систему S2, то  .
.
Следствие 9.4.11. Если в линейном пространстве K V система M из m элементов имеет ранг r, то любая ее подсистема S из s элементов (  ) имеет ранг не меньше чем r+s-m.
) имеет ранг не меньше чем r+s-m.
Доказательство. Действительно, если R - максимальная линейно независимая подсистема в M, |R|= r, то  , и поэтому
, и поэтому 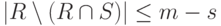 . Следовательно,
. Следовательно, 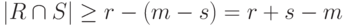 .
.
Следствие 9.4.12. Для системы строк 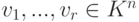 следующие условия эквивалентны:
следующие условия эквивалентны:
- система строк v1,...,vr является базисом линейного пространства строк Kn (т. е. максимальной линейно независимой подсистемой строк в K^n ; и тогда r=n );
- каждая строка
 единственным образом представляется в виде линейной комбинации(и тогда r=n );
единственным образом представляется в виде линейной комбинации(и тогда r=n );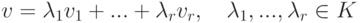
- r=n и система строк v1,...,vn линейно независима;
-
r=n и каждая строка
 представима в виде линейной комбинации
представима в виде линейной комбинации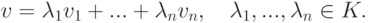
Доказательство. Мы уже показали, что  . Покажем, что
. Покажем, что  . Если v1,...,vr - линейно зависимая система строк,
. Если v1,...,vr - линейно зависимая система строк,  с некоторым
с некоторым  , то нулевая строка имеет два различных представления
, то нулевая строка имеет два различных представления
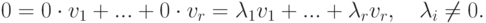
Ясно, что  . Покажем, что
. Покажем, что  . Для любой строки
. Для любой строки  система строк v1,...,vn,v линейно зависима ( n+1>n ). Так как v1,...,vn - линейно независимая система, то
система строк v1,...,vn,v линейно зависима ( n+1>n ). Так как v1,...,vn - линейно независимая система, то  для некоторых
для некоторых 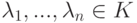 .
.
Ясно, что  . Покажем, что
. Покажем, что  . Допустим, что v1,...,vn - линейно зависимая система. Тогда ее максимально линейно независимая подсистема
. Допустим, что v1,...,vn - линейно зависимая система. Тогда ее максимально линейно независимая подсистема 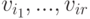 , r<n, является максимальной линейно независимой подсистемой в Kn, что противоречит r=n.
, r<n, является максимальной линейно независимой подсистемой в Kn, что противоречит r=n.
