НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 4: Линейное пространство M

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Теорема 8.5.3 (об определителе произведения матриц). Для любых квадратных матриц $A,B\in M_{n}(K)$ имеем |AB|=|A|,|B|.

Доказательство. Пусть C=AB. Рассмотрим определитель размера $2n\times 2n :$

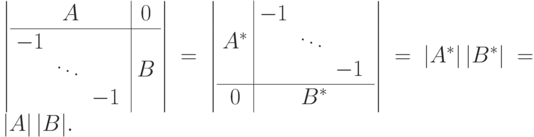
$\left| \begin{array}{c|c} A & 0\\ \hline \begin{matrix} -1\\ & \ddots\\ & & -1 \end{matrix} & B \end{array}\right| = \left|\begin{array}{c|c} A^* & \begin{matrix} -1\\ & \ddots\\ & & -1 \end{matrix} \\ \hline 0 & B^* \end{array}\right| = %{} %\\ %{}= |A^*|\, |B^*| = |A|\, |B|.$

С другой стороны, прибавляя к каждому столбцу, проходящему через матрицу B, соответствующую линейную комбинацию столбцов, проходящих через матрицу A, т. е.

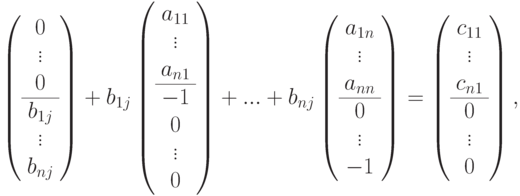
$\left( \begin{array}{c} 0\\ \vdots\\ 0\\ \hline b_{1j}\\ \vdots\\ b_{nj} \end{array} \right) + b_{1j} \left( \begin{array}{c} a_{11}\\ \vdots\\ a_{n1}\\ \hline -1\\ \phm 0\\ \vdots\\ \phm 0 \end{array} \right) +...+ b_{nj} \left( \begin{array}{c} a_{1n}\\ \vdots\\ a_{nn}\\ \hline \phm 0\\ \vdots\\ -1 \end{array} \right) = \left( \begin{array}{c} c_{11}\\ \vdots\\ c_{n1}\\ \hline 0\\ \vdots\\ 0 \end{array} \right),$

получаем, что

$\begin{mult} \left|\begin{array}{c|c} A & 0\\ \hline \begin{matrix} -1\\ & \ddots\\ & & -1 \end{matrix} & B \end{array}\right| = \left|\begin{array}{c|c} A & C=AB\\ \hline \begin{matrix} -1\\ & \ddots\\ & & -1 \end{matrix} & 0 \end{array}\right| ={} \\ {}= (-1)^n \left| \begin{array}{c|c} \begin{matrix} -1\\ & \ddots\\ & & -1 \end{matrix} & 0\\ \hline A & C \end{array}\right| = (-1)^{2n}|C|=|C|. \end{mult}$

Следствие 8.5.4.

Если $A,B\in M_{n}(K)$ , то |AB|=|A|,|B|=|BA| (т. е. хотя матрицы AB и BA могут быть различны, их определители равны).
|A^k|=|A|^k для $k\in N$ .

Упражнение 8.5.5. Покажите, что любые две матрицы в M₂( Z), коммутирующие с

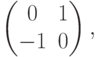
$\begin{pmatrix} \phm 0 & 1\\ -1 & 0 \end{pmatrix},$

коммутируют между собой.

Упражнение 8.5.6. Если

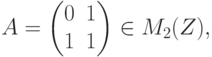
$A= \begin{pmatrix} 0 & 1\\ 1 & 1 \end{pmatrix} \in M_{2}( Z),$

то

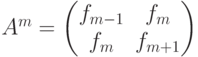
$A^m= \begin{pmatrix} f_{m-1} & f_m\\ f_m & f_{m+1} \end{pmatrix}$

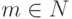для $m\in N$ , где

$\begin{gathe} f_0=0,\quad f_1=1,\quad f_2=1,\quad f_3=2,\\ f_{m+1}=f_m+f_{m-1} \end{gathe}$

(числа Фибоначчи). Если

$B = \begin{pmatrix} -\frac{\lambda_2}{5} & \frac{1}{5}\\[3\jot] -\sqrt{5}\lambda_1 & \sqrt{5} \end{pmatrix},$

где

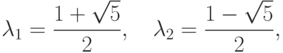
$\lambda_1=\frac{1+\sqrt{5}}{2},\quad \lambda_2=\frac{1-\sqrt{5}}{2},$

то

$A=B^{-1} \begin{pmatrix} \lambda_1 & 0\\ 0 & \lambda_2 \end{pmatrix} B,$

и поэтому

$A^m=B^{-1} \begin{pmatrix} \lambda_1^m & 0\\ 0 & \lambda_2^m \end{pmatrix} B,$

откуда

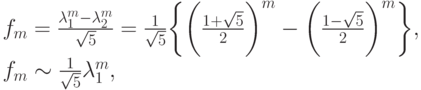
$\begin{gathe} f_m=\frac{\lambda_1^m-\lambda_2^m}{\sqrt{5}}= \frac{1}{\sqrt{5}} \biggl\{\biggl(\frac{1+\sqrt{5}}{2}\biggr)^m- \biggl(\frac{1-\sqrt{5}}{2}\biggr)^m\biggr\},\\ f_m\sim \frac{1}{\sqrt{5}}\lambda_1^m, \end{gathe}$

поскольку

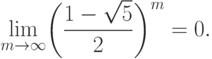
$\lim\limits_{m\to\infty} \biggl(\frac{1-\sqrt{5}}{2}\biggr)^m=0.$

Упражнение 8.5.7. Пусть $A\in M_{n}(K)$ . Покажите, что

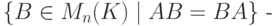
$\{B\in M_{n}(K)\mid AB=BA\}\text{ -}$

подалгебра в алгебре матриц M_n(K).

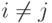Упражнение 8.5.8. Если $D=d(\lambda_1,...,\lambda_n)\in M_{n}(K)$ , $\lambda_i\neq \lambda_j$ при $i\neq j$ , $A\in M_{n}(K)$ и DA=AD, то A - также диагональная матрица.

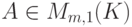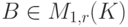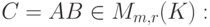
Упражнение 8.5.9 (внешнее произведение векторов). Если $A\in M_{m,1}(K)$ , $B\in M_{1,r}(K)$ , то $C=AB\in M_{m,r}(K) :$

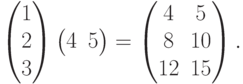
$\begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix} \begin{pmatrix} 4 & 5 \end{pmatrix} = \begin{pmatrix} 4 & 5\\ 8 & 10\\ 12 & 15 \end{pmatrix}.$

Упражнение 8.5.10. (скалярное произведение векторов) Если $A\in M_{1,n}(K)$ , $B\in M_{n,1}(K)$ , то $C=AB\in M_{1}(K)=K :$

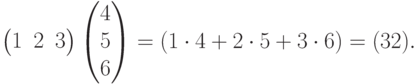
$\begin{pmatrix} 1 & 2 & 3 \end{pmatrix} \begin{pmatrix} 4\\ 5\\ 6 \end{pmatrix} = (1\cdot 4+2\cdot 5+3\cdot 6)=(32).$

Упражнение 8.5.11. Пусть 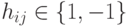$H=(h_{ij})\in M_{n}( R)$ , $h_{ij}\in \{1,-1\}$ , H^*H=nE,(=HH^*) (такая матрица называется матрицей Адамара). Например,

$\begin{pmatrix} 1 & \phm 1\\ 1 & -1 \end{pmatrix},\quad \begin{pmatrix} 1 & \phm 1 & \phm 1 & \phm 1\\ 1 & -1 & \phm 1 & -1\\ 1 & \phm 1 & -1 & -1\\ 1 & -1 & -1 & \phm 1 \end{pmatrix}.$

Докажите, что для n, отличных от 1, 2 и 4k, где $k\in N$ , не существует матриц Адамара.

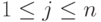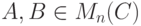Упражнение 8.5.12. Пусть $A=(a_{ij})\in M_{n}( C)$ - матрица Маркова (это означает, что для каждого j, $1 \leq j \leq n$ , $\sum\limits_{i=1}^{n}a_{ij}=1$ , т. е. сумма элементов по каждому столбцу равна 1 ). Докажите, что если $A,B\in M_{n}( C)$ - матрицы Маркова, то

AB и A^k, $k\in N$ , - матрицы Маркова;
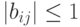если $|a_{ij}| \leq 1$ и $|b_{ij}| \leq 1$ для всех i, j, то $|c_{ij}| \leq 1$ для всех i, j для матрицы (c_ij}=C=AB.

Дальше >>

Алгебра матриц и линейные пространства

Линейное пространство M_m,n (K) прямоугольных матриц размера mxn

Вопросы и ответы

Авторизоваться

Алгебра матриц и линейные пространства

Линейное пространство M_m,n (K) прямоугольных матриц размера mxn

Вопросы и ответы