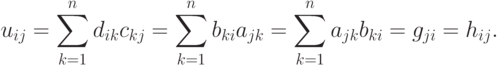НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 4: Линейное пространство M

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3991 / 731 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Итоговая теорема об алгебре матриц

Теорема 8.5.1.

I. Совокупность M_m,n(K) прямоугольных матриц размера $m\times n$ над K (в частности, квадратные матрицы M_n(K) ) относительно операции сложения образуют абелеву коммутативную группу, т. е.

I.1) операция сложения ассоциативна;

I.1') операция сложения коммутативна (т. е. A+B=B+A для всех $A,B\in M_{m,n}(K)$ );

I.2) существует нейтральный элемент 0 (нулевая матрица), 0+A=A+0=A для всех $A\in M_{m,n}(K)$ ;

I.3) для каждой матрицы $A\in M_{m,n}(K)$ существует противоположный элемент -A,(=(-1)A),=(-a_ij), A+(-A)=0.

II. Операции умножения матрицы A на элемент $c\in K$ , $A\mapsto cA$ , в M_m,n(K) удовлетворяют условиям:

II.1) $1\cdot A=A$ ;

II.2) (c₁c₂)A=c₁(c₂A).

III. Операции сложения и умножения на элементы 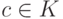$c\in K$ в M_m,n(K) удовлетворяют условиям

III.1) c(A+B)=cA+cB ;

III.2) (c₁+c₂)A=c₁A+c₂A.

Таким образом, I, II, III означают, что M_m,n(K) - линейное пространство над полем K.

IV. С операциями сложения A+B и умножения матриц AB совокупность квадратных матриц M_n(K) является кольцом, т. е.

IV.1) по сложению M_n(K) - абелева группа;

IV.2) с умножением матриц M_n(K) - моноид, т. е.

2.а) умножение матриц ассоциативно, (AB)C=A(BC) для любых 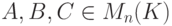$A,B,C\in M_{n}(K)$ ;

2.б) единичная матрица E является нейтральным элементом для операции умножения, AE=A=EA для всех $A\in M_{n}(K)$ ;

IV.3 операции сложения и умножения матриц удовлетворяют законам дистрибутивности

3.а) (A+B)C=AC+BC ;

3.б) C(A+B)=CA+CB.

V. С операциями сложения A+B и умножения AB матриц и операциями умножения cA матрицы A на элемент 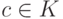$c\in K$ квадратные матрицы M_n(K) являются алгеброй , т. е.

V.1) кольцом (относительно сложения и умножения матриц);

V.2) линейным пространством (относительно сложения матриц и умножений матрицы на элемент K )

и дополнительно

V.3) (cA)B=c(AB)=A(cB) для $c\in K$ , $A,B\in M_{n}(K)$ .

Доказательство свойства V.3. Для любого места (i,j) имеем

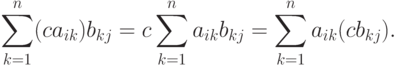
$\sum_{k=1}^{n}(ca_{ik})b_{kj}= c\sum_{k=1}^{n}a_{ik}b_{kj}= \sum_{k=1}^{n}a_{ik}(cb_{kj}).$

Теорема 8.5.2 (о транспонировании произведения матриц). Пусть

$A\in M_{m,n}(K),\quad B\in M_{n,r}(K),$

тогда (AB)^*=B^*A^*.

Доказательство. Ясно, что $G=AB\in M_{m,r}(K)$ и $H=G^*=(AB)^*\in M_{r,m}(K)$ . Так как $D=B^*\in M_{r,n}(K)$ и $C=A^*\in M_{n,m}(K)$ , то произведение U=B^*A^* существует и лежит в M_r,m(K), как и $(AB)^*\in M_{r,m}(K)$ .