Решение обыкновенных дифференциальных уравнений и систем

9.2 Численные методы решения дифференциальных уравнений и их реализация

Численные методы решения дифференциального уравнения первого порядка будем рассматривать для следующей задачи Коши. Найти решение дифференциального уравнения

( 9.4)

удовлетворяющее начальному условию

( 9.5)

иными словами, требуется найти интегральную кривую , проходящую через заданную точку (рис. 9.1).

Для дифференциального уравнения -го порядка

( 9.6)

задача Коши состоит в нахождении решения x = x(t), удовлетворяющего уравнению (9.6) и начальным условиям

( 9.7)

Рассмотрим основные численные методы решения задачи Коши.

9.2.1 Решение дифференциальных уравнений методом Эйлера

При решении задачи Коши (9.4), (9.5) на интервале , выбрав достаточно малый шаг , построим систему равноотстоящих точек

( 9.8)

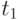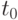Для вычисления значения функции в точке разложим функцию в окрестности точки в ряд Тейлора [2]

( 9.9)

При достаточном малом значении членами выше второго порядка можно пренебречь и с учётом получим следующую формулу для вычисления приближённого значения функции 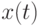в точке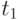

( 9.10)

Рассматривая найденную точку , как начальное условие задачи Коши запишем аналогичную формулу для нахождения значения функции 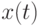в точке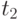

Повторяя этот процесс, сформируем последовательность значений в точках 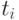по формуле

( 9.11)

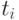Процесс нахождения значений функции в узловых точках по формуле (9.11) называется методом Эйлера. Геометрическая интерпретация метода Эйлера состоит в замене интегральной кривой 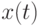ломаной с вершинами . Звенья ломанной Эйлера в каждой вершине имеют направление , совпадающее с направлением интегральной кривой 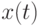уравнения (9.4), проходящей через точку (рис. 9.2). Последовательность ломанных Эйлера при на достаточно малом отрезке стремится к искомой интегральной кривой.

Рис. 9.2. Геометрическая интерпретация метода Эйлера

На каждом шаге решение 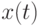определяется с ошибкой за счёт отбрасывания членов ряда Тейлора выше первой степени, что в случае быстро меняющейся функции 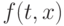может привести к быстрому накапливанию ошибки. В методе Эйлера следует выбирать достаточной малый шаг .