НОУ ИНТУИТ | Введение в Octave. Лекция 9: Решение обыкновенных дифференциальных уравнений и систем

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 582 / 64 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

9.2.4 Решение дифференциальных уравнений методом прогноза-коррекции Адамса

Рассмотрим решение уравнения (9.1)–(9.2) на интервале $[t_{i},t_{i+1}]$ . Будем считать, что решение в точках $t_{0},t_{1},t_{2},\dots,t_{i}$ уже найдено, и значения в этих точках будем использовать для нахождения значения $x(t_{i+1})$ .

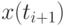Проинтегрируем уравнение (9.1) на интервале $[t_{i},t_{i+1}]$ и получим соотношение [2]

$x(t_{i+1})=x(t_{i})+\int _{t_{i}}^{t_{i+1}}f(t,x(t))\,dt$

( 9.20)

При вычислении интеграла, входящего в (9.20), вместо функции 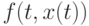f (t, x(t)) будем использовать интерполяционный полином Лагранжа,построенный по точкам 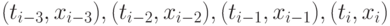$(t_{i-3},x_{i-3}), (t_{i-2},x_{i-2}), (t_{i-1},x_{i-1}),(t_{i},x_{i})$ . Подставив полином Лагранжа в (9.20), получаем первое приближение (прогноз) $\tilde{x}_{i+1}$ для значения функции в точке $t_{i+1}$

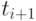
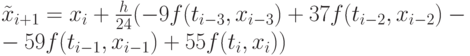$\tilde {x}_{i+1}=x_{i}&+\frac{h}{24}(-9f(t_{i-3},x_{i-3})+37f(t_{i-2},x_{i-2})-\\&-59f(t_{i-1},x_{i-1})+55f(t_{i},x_{i}))$

( 9.21)

Как только $\tilde{x}_{i+1}$ вычислено, его можно использовать. Следующий полином Лагранжа для функции f (t, x(t)) построим по точкам $(t_{i-2},x_{i-2}),(t_{i-1},x_{i-1}),(t_{i},x_{i})$ и новой точке $(t_{i+1},\tilde{x}_{i+1})$ , после чего подставляем его в (9.20) и получаем второе приближение (корректор)

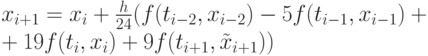$x_{i+1}=x_{i}+\frac{h}{24}(&f(t_{i-2},x_{i-2})-5f(t_{i-1},x_{i-1})+\\&+19f(t_{i},x_{i})+9f(t_{i+1},\tilde{x}_{i+1}))$

( 9.22)

Таким образом, для вычисления значения 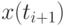$x(t_{i+1})$ методом Адамса необходимо последовательно применять формулы (9.21), (9.22) [2], а первые четыре точки можно получить методом Рунге-Кутта.

9.2.5 Решение дифференциальных уравнений методом Милна

Отличие метода Милна от метода Адамса состоит в использовании в качест ве интерполяционного полинома Ньютона.

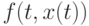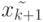Подставив в (9.20) вместо функции f (t, x(t)) интерполяционный полином Ньютона, построенный по точкам $(t_{k-3},x_{k-3}),(t_{k-2},x_{k-2}),(t_{k-1},x_{k-1}),(t_{k},x_{k})$ получаем первое приближение — прогноз Милна $\tilde {{x_{k+1}}}$ для значения функции в точке 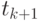$t_{k+1}$ [2]

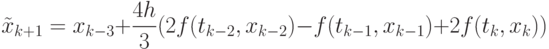$\tilde {x}_{k+1}=x_{k-3}+\frac{4h}{3}(2f(t_{k-2},x_{k-2})-f(t_{k-1},x_{k-1})+2f(t_{k},x_{k}))$

( 9.23)

Следующий полином Ньютона для функции 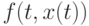f (t, x(t)) построим по точкам 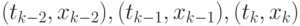$(t_{k-2},x_{k-2}),(t_{k-1},x_{k-1}),(t_{k},x_{k})$ и новой точке 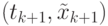$(t_{k+1},\tilde{x}_{k+1})$ , после чего подставляем его в (9.20) и получаем второе приближение — корректор Милна [2]

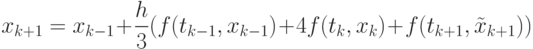$x_{k+1}=x_{k-1}+\frac{h}{3}(f(t_{k-1},x_{k-1})+4f(t_{k},x_{k})+f(t_{k+1},\tilde{x}_{k+1}))$

( 9.24)

В методе Милна для вычисления значения 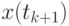$x(t_{k+1})$ необходимо последовательно применять формулы (9.23), (9.24), а первые четыре точки можно получить методом Рунге-Кутта.

Существует модифицированный метод Милна. В нём сначала вычисляется первое приближение по формуле (9.23), затем вычисляется управляющий параметр [2]

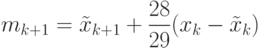$m_{k+1}=\tilde {x}_{k+1}+\frac{28}{29}(x_{k}-\tilde {x}_{k})$

( 9.25)

После чего вычисляется значение второго приближения — корректор Милна по формуле

$x_{k+1}=x_{k-1}+\frac{h}{3}(f(t_{k-1},x_{k-1})+4f(t_{k},x_{k})+f(t_{k+1},m_{k+1}))$

( 9.26)

В модифицированном методе Милна первые четыре точки можно получить методом Рунге-Кутта, а для вычисления значения 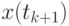$x(t_{k+1})$ необходимо последовательно применять формулы (9.23), (9.25), (9.26).

Дальше >>

Авторизоваться

Введение в Octave

Решение обыкновенных дифференциальных уравнений и систем

9.2.4 Решение дифференциальных уравнений методом прогноза-коррекции Адамса

9.2.5 Решение дифференциальных уравнений методом Милна

Вопросы и ответы