|
Возможна ли разработка приложения на Octave с GUI? |
Основы работы
2.5.5 Функции, определённые пользователем
В первой главе мы уже рассмотрели создание небольшой программы, которая решает конкретное квадратное уравнение. В этой программе отсутствовал заголовок (первая строка определённого вида), и в неё невозможно было передать входные параметры, то есть это был обычный список команд, воспринимаемый системой как единый оператор.
Функция, как и программа, предназначена для неоднократного использования, но она имеет входные параметры и не выполняется без их предварительного задания. Функция имеет заголовок вида
![function\ name1[,name2,... ] = fun(var1[,var2,... ])](/sites/default/files/tex_cache/99d8184c3548e56c7cd7f52413fd24f7.png)
где ![name1[,name2,... ]](/sites/default/files/tex_cache/cb71700575552070216b032f28314362.png) — список выходных параметров, то есть переменных, которым будет присвоен конечный результат вычислений,
— список выходных параметров, то есть переменных, которым будет присвоен конечный результат вычислений,  — имя функции,
— имя функции, ![var1[,var2,... ]](/sites/default/files/tex_cache/3753b15611d59e79551b4c184ba44737.png) — входные параметры. Таким образом простейший заголовок функции выглядит так:
— входные параметры. Таким образом простейший заголовок функции выглядит так:

Все имена переменных внутри функции, а также имена из списка входных и выходных параметров воспринимаются системой как локальные, то есть эти переменные считаются определёнными только внутри функции.
Программы и функции в Octave могут быть созданы при помощи текстового редактора и сохранены в виде файла с расширением .m или .M. Но при создании и сохранении функции следует помнить, что её имя должно совпадать с именем файла.
Вызов программ в Octave осуществляется из командной строки. Программу можно запустить на выполнение, указав имя файла, в котором она сохранена.
Обращение к функции осуществляется так же, как и к любой другой встроенной функции системы, то есть с указанием входных и выходных параметров. Вы можете вызвать функцию из командной строки или использовать её как один из операторов программы.
Пример 2.1. Создать функцию для решения кубического уравнения.
Кубическое уравнение
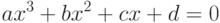
после деления на  принимает канонический вид:
принимает канонический вид:
 |
( 2.1) |
где 
В уравнении (2.1) сделаем замену

и получим следующее приведённое уравнение:
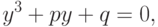 |
( 2.2) |
где 
Число действительных корней приведённого уравнения (2.2) зависит от знака дискриминанта  (табл. 2.10).
(табл. 2.10).
Корни приведённого уравнения могут быть рассчитаны по формулам Кардано:

| Дискриминант | Количество действительных корней | Количество комплексных корнейth |
|---|---|---|
D 0 0 |
1 | 3 |
| D<0 | 3 | - |
Здесь ![u=\sqrt[3]{\frac{-q}{2}+\sqrt{D}}, v =\sqrt[3]{\frac{-q}{2}-\sqrt{D}},](/sites/default/files/tex_cache/48601fbe86cfe32ad17644273958ca14.png)
Далее представлен список команд (листинг 2.1), реализующий описанный выше способ решения кубического уравнения:
>>> function [ x1, x2, x3]=cub (a, b, c, d) r=b/a; s=c /a; t=d/a; p=(3*s-r ^2) /3; q=2*r ^3/27-r*s/3+t; D=(p/3) ^3+(q /2) ^2; u=(-q/2+ sqrt (D)) ^(1/3); v=(-q/2-sqrt (D)) ^(1/3); y1=u+v; y2=-(u+v ) /2+(u-v ) /2*i*sqrt ( 3 ); y3=-(u+v ) /2 -(u-v ) /2*i*sqrt ( 3 ); x1=y1-r / 3; x2=y2-r / 3; x3=y3-r / 3; endfunction % Вычисляем корни уравненияЛистинг 2.1. Нахождение корней кубического уравнения (пример 2.1).>>> [x1, x2, x3]=cub(3, -2, -1, -4) x1 = 1.4905 x2 = -0.41191 + 0.85141i x3 = -0.41191 - 0.85141i
