|
Возможна ли разработка приложения на Octave с GUI? |
Основы работы
2.5.2 Комплексные числа. Функции комплексного аргумента
Рассмотрим реализацию комплексной арифметики в Octave. Как было отмечено выше, для обозначения мнимой единицы зарезервировано два имени —  , поэтому ввод комплексного числа производится в формате:
, поэтому ввод комплексного числа производится в формате:
действительная часть +  * мнимая часть
* мнимая часть
или
действительная часть +  * мнимая часть
* мнимая часть
Пример ввода и вывода комплексного числа:
>>> 3+i*5 ans = 3+5i >>> -2+3*i ans = -2 + 3i >>> 7+2*j ans = 7+2i >>> 0+7i ans = 0+7i >>> 6+0*j ans = 6
Кроме того, к комплексным числам применимы элементарные арифметические операции: +, -, *, \, /, ^; например:
>>> a= -5+2i; >>> b=3-5*i; >>> a+b ans = -2-3i >>> a-b ans = -8+7i >>> a*b ans = -5 + 31i >>> a/b ans = -0.73529-0.55882i >>> a^2+b^2 ans = 5-50i
Функции для работы с комплексными числами приведены в таблице 2.6.
| Функция | Описание функции |
|---|---|
 |
выдаёт действительную часть комплексного аргумента 
|
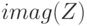 |
выдаёт мнимую часть комплексного аргумента 
|
 |
вычисляет значение аргумента комплексного числа  в радианах от в радианах от 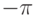 до до 
|
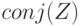 |
Выдаёт число, комплексно сопряжённое 
|
Примеры использования функций из таблицs 2.6.:
>>> a=-3;b=4;Z=a+b*i Z = -3+4i >>> real(Z) ans = -3 >>> imag(Z) ans = 4 >>> angle(Z) ans = 2.2143 >>> conj(Z) ans = -3-4i
Обратите внимание, что большая часть математических функций, описанных в п. 2.5.1, работают с комплексным аргументом:
>>> a=-3; >>> b=4; >>> Z=a+b*i Z = -3+4i >>> sin(Z) ans = -3.8537-27.0168i >>> exp(Z) ans = -0.032543-0.037679i >>> sqrt(Z) ans = 1+2i >>> abs(Z) ans = 5
2.5.3 Операции отношения
Операции отношения выполняют сравнение двух операндов и определяют, истинно выражение или ложно (таблица 2.7). Результат операции отношения — логическое значение. В качестве логических значений в Octave используются 1 ("истина") и 0 ("ложь").
| Операция | Описание операции |
|---|---|
| < | меньше |
| > | больше |
| == | равно |
| ~= | не равно |
| <= | меньше или равно |
| <= | больше или равно |
| A | B |  |
A & B | 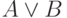 |
 |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 |
| Тип выражения | Выражение | Логический оператор | Логическая операция |
|---|---|---|---|
| Логическое "и" | A and B | and(A, B) | A & B |
| Логическое "или" | A or B | or(A, B) | A | B |
| Исключающее "или" | A xor B | xor(A,B) | |
| Отрицание | not A | not (A) | ~A |
2.5.4 Логические выражения
Логическое выражение может быть составлено из операций отношения и логических операций (операторов). Логические выражения выполняются над логическими данными. В таблице 2.8 представлены основные логические выражения: "и", "или", "не".
В Octave существует возможность представления логических выражений в виде логических операторов и логических операций (таблица 2.9).
В таблице 2.9)  и
и  — логические выражения (или целочисленные значения 1 и 0).
— логические выражения (или целочисленные значения 1 и 0).
Логические операторы (выражения) определены и над массивами (матрицами) одинаковой размерности и выполняются поэлементно над элементами. В итоге формируется результирующий массив (матрица) логических значений, каждый элемент которого вычисляется путём выполнения логической операции над соответствующими элементами исходных массивов. При одновременном использовании в выражении логических и арифметических операций возникает проблема последовательности их выполнения. В Octave принят следующий приоритет операций.
- Логические операторы.
- Логическая операция ~.
- Транспонирование матриц, операции возведения в степень, унарный + и -.
- Умножение, деление
- Сложение, вычитание.
- Операции отношения.
- Логическая операция "и" — &
- Логическая операция "или" — |
Ниже представлены примеры использования логических операций над скалярными и матричными значениями.
>>> A=3;B=4;C=2*pi; >>> P=~(((A+B)*C)>A^B) | (A+B) ==((B-A)+A^2) P = 1 >>> X=[2 1 6]; Y=[1 3 5]; >>> Z=~or ((X>2*Y), (X>Y)) | and ((X>2*Y), (X<Y)) Z = 0 1 0
