Матрицы
Представим вектор  как линейную комбинацию векторов
как линейную комбинацию векторов 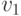 и
и 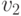 :
: 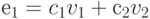 :
:
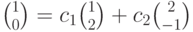
Получаем два уравнения с двумя неизвестными: 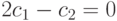 и
и  Решая уравнения получаем:
Решая уравнения получаем: 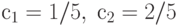 . Теперь, зная трансформации векторов
. Теперь, зная трансформации векторов 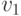 и
и 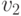 можно вычислить трансформацию вектора
можно вычислить трансформацию вектора  :
:
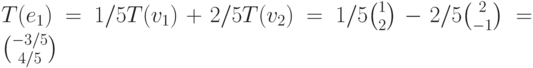
Подобным образом находим  . Рассматривая
. Рассматривая  и
и  как столбцы матрицы Т, получим:
как столбцы матрицы Т, получим:
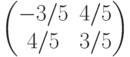
В классических вычислениях сложные задачи не решаются за один шаг Типично для достижения ответа требуется выполнить последовательность операций. Подобным образом и квантовый алгоритм проектируется не как единственная линейная трансформация, а как композиция нескольких простых линейных трансформаций.
Прежде всего, нам нужно выяснить, как вычислить матрицу композиции  линейных трансформаций, если известны матрицы трансформаций Т и S.
линейных трансформаций, если известны матрицы трансформаций Т и S.
Начнем обсуждение с соглашения о порядке операций. Традиционно для математики записывать аргумент функции f (х) или линейной трансформации Т(v) справа от имени функции. Композиция  , когда она применяется к вектору v дает
, когда она применяется к вектору v дает  . Это означает, что в композиции
. Это означает, что в композиции  множитель, который стоит справа, применяется первым.
множитель, который стоит справа, применяется первым.
Пусть Т и S - две линейные трансформации с матрицами А и В соответственно. Нам необходимо вычислить матрицу С композиции  . Напомним, что k-й столбец матрицы С - образ
. Напомним, что k-й столбец матрицы С - образ 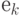 при трансформации
при трансформации  :
: 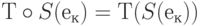 . Однако,
. Однако,  -это просто k-й столбец матрицы В. Отсюда следует, что k-й столбец С - это произведение матрицы А на k-й столбец В. Матрицу С, вычисляемую таким образом, назовем произведением матриц А и В: С = АВ.
-это просто k-й столбец матрицы В. Отсюда следует, что k-й столбец С - это произведение матрицы А на k-й столбец В. Матрицу С, вычисляемую таким образом, назовем произведением матриц А и В: С = АВ.
Например,
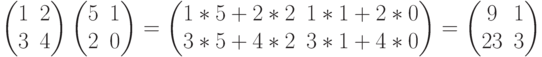
Нетрудно заметить, что элемент матрицы произведения С, стоящий на пересечении строки с индексом m и столбца с индексом k, является скалярным произведением строки с индексом m матрицы А и столбца с индексом k матрицы В.
Подводя итог, - матрица композиции двух линейных трансформаций является произведением матриц этих трансформаций.
Мы можем также определить сумму двух матриц размера N * N, где элемент с индексами m и k матрицы суммы представляет сумму элементов с теми же индексами матриц слагаемых:
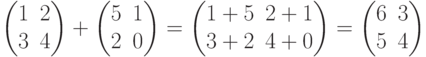
Некоторые алгебраические свойства матричных операций совпадают со свойствами чисел: А(В + С) = АВ + АС, (А + В)С = АС + ВС. Однако, есть важная разница. Рассмотрим две матрицы:
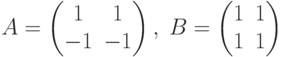
Вычислим произведение АВ и ВА:
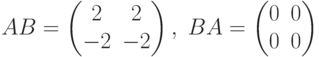
Этот пример показывает, что произведение матриц не коммутативно:  .
.
Этот пример также показывает, что произведение ненулевых матриц может быть нулевой матрицей.
Все же произведение матриц обладает свойством ассоциативности (АВ)С = А(ВС). Это следует из того факта, что умножение матриц соответствует композиции линейных трансформаций  , так как обе стороны, примененные к вектору v, дают один и тот же результат:T(S(R(v)))
, так как обе стороны, примененные к вектору v, дают один и тот же результат:T(S(R(v)))
В заключение этой лекции рассмотрим одно из применений линейной алгебры к задачам тригонометрии. Рассмотрим композицию поворота на угол  и поворота на угол
и поворота на угол  . Очевидно
. Очевидно
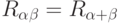
Выпишем эквивалентное соотношение для матриц поворота:
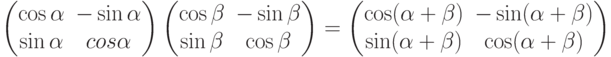
Произведение матриц в левой части равенства дает:
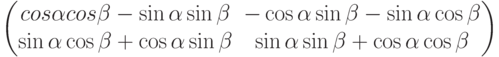
Сравнивая полученный результат с матрицей правой части равенства, приходим к известному тригонометрическому тождеству:
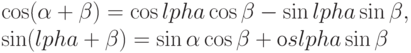
И это наиболее экономичное доказательство этой важной формулы.
