НОУ ИНТУИТ | Квантовые вычисления. Лекция 2: Квантовая механика, частично лишенная мифического ореола

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 03.06.2019 | Доступ: свободный | Студентов: 506 / 76 | Длительность: 09:11:00

Темы: Программирование, Математика, Физика, Суперкомпьютерные технологии

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

В этой лекции мы обсудим аксиоматику квантовой механики. Со времен Ньютона понятие физического объекта описывалось с помощью числовых характеристик, таких как позиция объекта, его скорость и ускорение. Физические теории давали точное предсказание будущей траектории движения объекта, если известны начальные условия и все силы, действующие на объект. Квантовая механика утверждает, что будущее не является полностью определенным. Она постулирует, что мы можем предсказать будущие события лишь с некоторой вероятностью, и что неопределенность следует из законов природы.

Состояние квантовой системы - это вектор длины 1 в пространстве состояний. Для наших целей квантовых вычислений мы будем рассматривать это пространство как 2^n -мерное пространство n-кубита для некоторого значения n. Пространство n-кубита является 2^n -мерным пространством, поскольку каждый n-кубит имеет 2^n компонент, также как в 3-х мерном пространстве каждый вектор имеет 3 компоненты. В общем случае, в квантовой механике пространство может иметь любую размерность и быть даже бесконечномерным пространством. Более того, в общепринятой формализации квантовой механики компоненты векторов являются комплексными числами, но мы для простоты рассмотрения ограничиваемся ситуацией, когда компоненты представлены вещественными числами.

В классической механике траектория движения объекта описывается вторым законом Ньютона, математически представленным в виде дифференциального уравнения. Второй закон Ньютона гласит, что произведение массы на ускорение равно силе, действующей на объект, а ускорение является второй производной от позиции объекта. Таким образом мы получаем уравнение для второй производной, представляющее дифференциальное уравнение.

В квантовой механике эволюция квантовой системы также описывается некоторым дифференциальным уравнением, называемым уравнением Шредингера. Уравнение Шредингера само по себе для нашего изложения не так важно, поэтому мы не будем выписывать его непосредственно. Для нас более важен тот факт, что эволюция замкнутой квантовой системы задается ортогональными линейными трансформациями. В следующей лекции мы детально объясним, что представляют собой эти трансформации.

Вероятностная природа квантовой механики проявляется в процессе измерений. Измерение является единственным способом извлечения данных, определяющих квантовое состояние.

Рассмотрим n-кубит

$\sum^{2^n-1}_{k=0}a_k|k\rangle$

с нормализацией (длина вектора равна 1)

$\sum^{2^n-1}_{k=0}a^2_k=1$

Когда мы будем вьполнять измерение состояния этого кубита, то получим одно из классических значений совокупности n битов от 000...0 до 111...1, где значение k (в двоичном представления) появится с вероятностью а^2_k . Условие нормализации говорит, что сумма вероятностей всех возможных событий равна 1, как и должно быть.

Для проведения измерений мы должны активно воздействовать на квантовую систему В результате сразу же после измерения квантовая система разрушается. После измерения квантовая система переходит в чистое состояние, соответствующее наблюденному значению.

Например, если мы выполним измерение для 2-кубита

$0.3|00\rangle +0.1|01\rangle +0.9|10\rangle +0.3|11\rangle$

то возможны 4 исхода:

С вероятностью 0.09 мы получим значение "00" и 2-кубит перейдет в чистое состояние Х00}.
С вероятностью 0.01 мы получим значение "01" и 2-кубит перейдет в чистое состояние $|01\rangle$ .
С вероятностью 0.81 мы получим значение "10" и 2-кубит перейдет в чистое состояние $|10\rangle$ .
С вероятностью 0.09 мы получим значение "11" и 2-кубит перейдет в чистое состояние $|11\rangle$

Зачастую нам требуется измерить состояние лишь некоторых кубитов в большом n-кубите. Давайте обсудим, что происходит в подобной ситуации. Предположим у нас есть 3-кубит:

Мы хотим измерить состояние первых двух битов кубита, но не трогать третий бит. Для первых двух битов возможны 4 наблюдаемых состояния: 00, 01, 10 и 11. Каковы вероятности возможных исходов? После измерения первые два бита получат определенные значения, значение третьего бита не будет фиксировано. Вероятность наблюдения для первых двух битов значения "00" определяется коэффициентами первых двух термов в записи 3-кубита: 0.09 + 0.36 = 0.45 . Для нормализации состояния третьего не наблюдаемого бита необходимо коэффициенты этих двух термов разделить на корень квадратный из вероятности появления данного исхода. В нашем примере получим следующие результаты:

С вероятностью мы наблюдаем "00" и новое состояние системы: $1/\sqrt{0.45}(0.3|000\rangle - 0.6 |001\rangle)$ .
С вероятностью мы наблюдаем " 01" и новоe состояние системы: $1/\sqrt {0.5}(-0.1 |010\rangle - 0.7 |011\rangle)$ .
С вероятностью 0.01 мы наблюдаем " 10" и новое состояние системы: $|101\rangle$ .
С вероятностью 0.04 мы наблюдаем " 11" и новое состояние системы: - $|110\rangle$ .

Заметьте, учитывая особенности нашего 3-кубита, в последних двух случаях вероятность того, что третий бит соответственно принимает значения 1 и 0, равна 1.

Опишем теперь, как можно реализовать процедуру измерения, используя поляризационные фильтры. Мы можем использовать зеркально подобный поляризационный фильтр, который отражает свет с горизонтальной поляризацией $|10\rangle$ и позволяет пропускать свет с вертикальной поляризацией $|10\rangle$ . Что произойдет, когда фотон с линейной поляризацией под углом а проходит через этот фильтр? Нельзя в точности предсказать, что произойдет с фотоном, поскольку исход эксперимента носит вероятностный характер. Начальное состояние фотона:

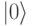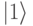$\соs(\alpha) |10\rangle + \sin(\alpha) |1\rangle$

С вероятностью $\cos^2 (\alpha)$ фотон отразится и изменит свою поляризацию на горизонтальную $|0\rangle$ , с вероятностью $\sin^2(\alpha)$ фотон пройдет через фильтр и изменит свою поляризацию на вертикальную $|1\rangle$ .

Если вынуть фильтры, применяемые в 3D очках, и поместить друг против друга эти два поляризованных фильтра, то можно заметить, что в одном положении они будут совершенно прозрачными, но стоит один фильтр повернуть на 90 градусов относительно другого, то свет будет блокирован. При вращении прозрачность постепенно меняется и в соответствии с приведенным выше объяснением интенсивность проходящего света пропорциональна $\соs^2 (\аlpha)$ , где $\alphа$ - угол между осями фильтра.

В общем случае схема квантовых вычислений состоит из трех этапов:

Инициализация. Задавая значения n-кубита квантового компьютера, кодируем входные данные алгоритма. Можно все начальные значения положить равными $|00 \dots 0\rangle$ , если вход встроен в сам алгоритм.
Выполнение квантового алгоритма. На этом этапе выполняются сложные ортогональные линейные трансформации. Вычисления на классическом компьютере в конечном итоге сводятся к элементарным операциям бинарной логики, вьполняемых над одним или парой битов. Точно также квантовый алгоритм расщепляется на элементарные квантовые операции, каждая из которых выполняется над одним кубитом или парой кубитов.
Выполнение измерений заключительного состояния квантовой системы.

Дальше >>

Авторизоваться

Квантовые вычисления

Квантовая механика, частично лишенная мифического ореола

Вопросы и ответы