Сложные проценты

3.6 Используем Excel

Продолжим изучение возможностей программы Excel, которые используются при решении финансовых задач. При решении примеров из лекции 1 мы обсудили (и использовали) ввод данных с форматированием и работу с простыми формулами в Excel. В этой лекции мы будем дополнительно использовать библиотеку встроенных функций. За деталями организации доступа к встроенным функциям Excel и использования команды Формат ячейки мы отсылаем читателя к специализированной литературе. Заметим, что использование встроенных функций в Excel ничем, по существу, не отличается от их использования в любом популярном языке программирования.

Напомним читателю, что, для того чтобы решения примеров в Excel выглядели также, как на рисунках в этих лекциях, необходимо установить в ячейках правильные форматы. Мы не указываем здесь точное место команды форматирования ячеек, так как допускаем, что читатели могут использовать любые версии программы Excel, но не ранее XP.

Рис. 6. Пример на вычисление сложного процента

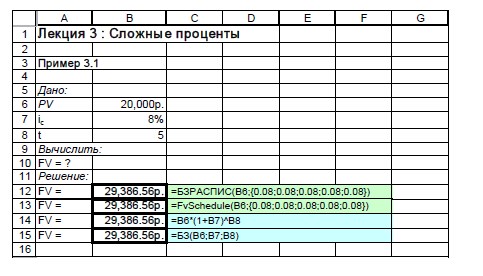
На рис.6 приведен фрагмент рабочего листа с решением примера 34. Сумма, которая будет на счёте в банке через 5 лет (29 386.56 руб.), определена четырьмя способами: значение в ячейке B12 вычислено с помощью встроенной функции БЗРАСПИС; значение в ячейке B13 вычислено с помощью англоязычного аналога той же встроенной функции FVSchedule; значение в ячейке B15 вычислено с помощью функции пользователя БЗ (о ней будет рассказано далее); значение в ячейке B14 - непосредственно по формуле сложных процентов (3.2).

Сделаем необходимые пояснения к приведенному решению примера 34. Заметим, что в Excel отсутствует встроенная функция, которая реализует вычисления по формуле

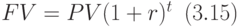
Неудобство из-за отсутствия встроенной функции, которая реализует вычисления по формуле (3.15), легко устранить, написав такую функция на языке VBA. Мы приведем только простейший вариант текста такой функции БЗ (листинг 3.1):

 Function БЗ(ПривСтоим, Процент, Срок)
  БЗ = ПривСтоим*(1 + Процент)^ Срок
 End Function
\end{verbatim}
\vspace{-0.35cm}

Использование функции, созданной пользователем, ничем не отличается от использования встроенной функции Excel, что и продемонстрировано при вычислении значения в ячейке B15. Однако следует иметь в виду две связанные с этим технические детали. Во-первых, при открытии xls-файла, в котором имеется хотя бы одна функция пользователя, программа Excel выдает запрос об открытии доступа к этим функциям. Во-вторых, для доступа к некоторой функции пользователя необходимо иметь открытым тот файл, в котором эта функция содержится.

Рис. 7. Пример на вычисление эффективной процентной ставки

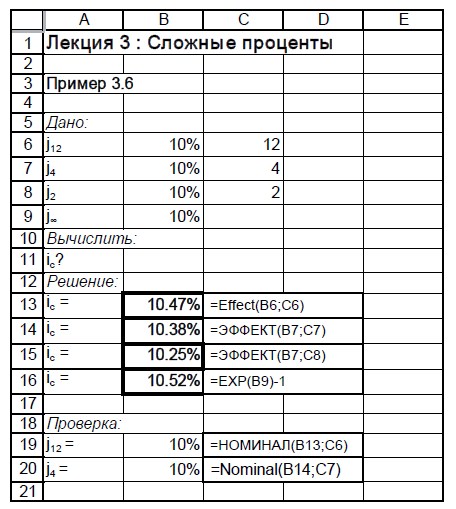
Покажем теперь, как выполнить решение другого типичного примера на сложные проценты средствами Excel. На рис. 7 приведен фрагмент рабочего листа с решением примера 39. Для вычисления эффективной процентной ставки 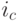при дискретном начислении процентов в Excel имеется встроенная финансовая функция ЭФФЕКТ, реализующая формулу:

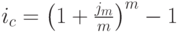
Напомним, что вычисление эффективной процентной ставки 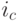при непрерывном начислении процентов выполняется по формуле: 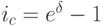. При записи вычислений по этой формуле в ячейке B17 была использована встроенная математическая функция EXP.

Имеется также встроенная финансовая функция НОМИНАЛ, которая по эффективной процентной ставке 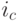и числу начисления процентов в период (m) вычисляет номинальную процентную ставку по формуле:

Список ключевых терминов

Множитель наращения - множитель, равный , где r - процентная ставка за период.

Непрерывное начисление процентов -схема начисления процентов, при которой наращенная за время t сумма S определяется формулой: .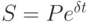

Период-временной промежуток, которому соответствует фиксированная процентная ставка.

Сила роста - параметр в формуле непрерывного начисления процентов.

Сложный процент - схема начисления процентов, при которой базой для следующего периода является исходная сумма плюс начисленные проценты.

Эффективная ставка - ставка сложных процентов, эквивалентная данной процентной ставке и не зависящая от срока применения этой ставки.

Краткие итоги

В лекции рассмотрено применение сложного процента в задачах оценивания финансовых объектов ранее определённых в этом курсе и операций с ними. Продолжен обзор возможностей программы Excel для решения рассмотренных в курсе примеров.