Сложные проценты
3.4 Эффективная процентная ставка
При заключении финансовых контрактов каждый участник сделки стремится заключить контракт на наиболее выгодных для себя условиях. Условия контракта могут быть различными, и надо иметь возможность сравнивать контракты. При этом различные контракты могут предусматривать различные виды начисления процентов, и для сравнения таких контрактов необходимо разработать способы приведения различных процентных ставок к одному виду. Для этой цели вводятся понятия: эквивалентность процентных ставок и эффективная процентная ставка.
Эффективной процентной ставкой, соответствующей данной процентной ставке, называется ставка сложных процентов 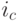 , эквивалентная данной процентной ставке и не зависящая от срока применения этой ставки.
, эквивалентная данной процентной ставке и не зависящая от срока применения этой ставки.
Формула для эффективной процентной ставки может быть выведена из следующего равенства:

Выполнив простые преобразования, получаем условия эквивалентности ставок 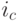 и
и  :
:

Аналогично выводится и эквивалентность любой пары ставок, например, 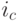 и
и  :
:

Вычисление эффективной процентной ставки применяется для определения реальной доходности финансовой операции. Эта доходность определяется соответствующей эффективной процентной ставкой. Рассмотрим примеры.
Пример 39. Банк выплачивает по вкладам 10% годовых (сложных). Какова реальная доходность вкладов в этом банке при следующих видах начисления процентов: а) ежемесячно, б) ежеквартально, в) по полугодиям, г) непрерывно?
Решение. Чтобы определить реальную доходность вкладов в банк, надо найти эффективную процентную ставку  при: а)
при: а)  , б)
, б)  , в)
, в)  , г)
, г)  . Применим теперь соответствующие формулы:
. Применим теперь соответствующие формулы:
- а) по формуле (3.10) получаем:

- б) по формуле (3.10) получаем:

- в) по формуле (3.10) получаем:
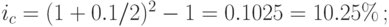
- г) по формуле (3.11) получаем:
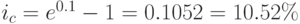
3.5 Плавающий сложный процент
В договорах срочного вклада обычно оговаривается, что в случае невостребования вкладчиком вклада по истечении его срока действия договор продлевается (пролонгируется) на очередной срок, равный сроку вклада. Проценты при очередном сроке вклада начисляются по ставке, действующей в банке для данного вида вкладов на день продления договора1 Мы дословно процитировали условия продления невостребованного вклада из текста договора срочного вклада одного из крупных российских банков.. Если процентная ставка изменяется в течение действия договора, то говорят, что применяется плавающая ставка процента.
При плавающей процентной ставке наращенная сумма за два срока вклада будет вычисляться по формуле:

где 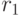 - процентная ставка за период по вкладу в первый срок,
- процентная ставка за период по вкладу в первый срок, 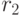 - процентная ставка за период по вкладу во второй срок, t - величина одного срока в периодах.
- процентная ставка за период по вкладу во второй срок, t - величина одного срока в периодах.
Если обобщить формулу (3.13) на k сроков и допустить, что сроки могут иметь различную длительность 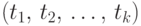 , то получим общую формулу плавающего сложного процента:
, то получим общую формулу плавающего сложного процента:
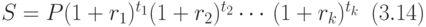
Плавающий сложный процент применяется на практике не только в договорах срочных вкладов, но и при выдаче ссуд и ипотеке. Применение плавающего процента свидетельствует о нестабильной обстановке на финансовом рынке. Рассмотрим следующий пример.
Пример 40. Два года назад вы заняли у приятеля 50\,000 руб. и собираетесь вернуть долг сейчас. Какую сумму справедливо вернуть приятелю, если инфляция в эти годы составила 16% и 11%? Под справедливостью подразумевается возможность купить на возвращенные деньги то же количество благ, что и два года назад на одолженные деньги.
Решение. Применяя формулу (32) при 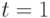 ,
,  ,
,  ,
,  , получаем:
, получаем:

