Математическая логика событий и логические нейронные сети
Учёные объяснения большей частью производят то впечатление, что бывшее ясно и понятно становится темно и запутанно.
Л.Н. Толстой. Дневники, 1900, сентябрь.
Исчерпывающее множество событий
Следующие ниже построения не могут не затронуть смысловых особенностей высказываний о событиях. Кроме чисто формальных свойств высказываний, выражающихся в их истинности или ложности, невозможно полностью абстрагироваться от содержательной сути или от контекста, в котором они звучат.
Определение 1.1. Исчерпывающее множество событий (ИМС) образуют те события, совокупность высказываний о которых покрывает весь возможный смысловой диапазон проявления объекта высказывания, и каждая допустимая ситуация характеризуется тем, что значение ИСТИНА (1) может принимать единственное высказывание из этой совокупности, а сумма вероятности этих событий равна единице.
Рассмотрим примеры.
- Времена года бывают: весна, лето, осень, зима.
- В состав редколлегии входят трое: Иванов, Петров, Сидоров. Тогда провозглашение одной из этих фамилий определяет выдвижение единственного представителя коллектива в президиум собрания. То есть, если Иванов, а затем и Петров взяли самоотвод, то однозначно в президиум направляется Сидоров.
- Наказуемое превышение скорости автомобиля делится на диапазоны: до 10%, от 10% до 20%, свыше 20%. Однако, если в регламентирующем документе заданы только диапазоны до 10% и от 10% до 100% (а что далее?), то это не будет соответствовать исчерпывающему множеству событий. Такие нестрогие определения возможного диапазона ситуаций являются причиной юридической казуистики, требующей дальнейшего исследования прецедента.
Итак, ИМС, которому соответствует множество высказываний А = {x1, ..., xn}, характеризуется тем, что при соответствующих обстоятельствах одно и только одно высказывание из этого множества может принимать значение 1. Это и определяется операцией ИСКЛЮЧАЮЩЕЕ ИЛИ, которую обозначим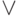 
. Говоря же о сумме вероятностей событий, мы несколько забежали вперёд.
Очевидны главные свойства высказываний о событиях из ИМС:
 |
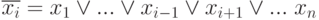( 1.1) |
 |
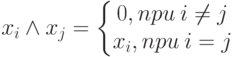( 1.2) |
Закономерен вопрос: может ли ИМС содержать единственное событие? В некоторых примерах применения логических нейронных сетей, рассмотренных в части II, например, при представлении фактора эффективности единственным рецептором, за величину его возбуждения принимается известное или испытываемое значение эффективности. Это позволяет сократить объём логической нейронной сети, "напрямую" задавая "одинокие" параметры исследуемых объектов.