Математическая логика событий и логические нейронные сети
Система принятия решений
Для некоторой логической функции f от переменных из факторного пространства событий воспользуемся операцией следования (импликации) и сформируем логическое выражение вида
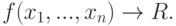 |
( 1.4) |
Здесь f следует рассматривать как выражение, определяющее условие, сложившуюся ситуацию, посылку, а R - высказывание, которое рассматривается как следствие: правило поведения, значение векторной функции, указание к действию и т.д. Таким образом, возможно формирование связей вида "посылка - следствие", "если - то". При этом функция f задаётся на множестве ситуаций и указывает на то, что, если на некоторой ситуации она принимает значение 1 (ИСТИНА), то такое же значение принимает высказывание R, являясь руководством к действию, к принятию определённого решения.
Подобно (1.3), можно описать множество логических выражений, определяющих стройную систему управления или принятия решений в соответствии со складывающейся ситуацией в факторном пространстве событий:
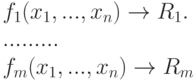 |
( 1.5) |
Определение 1.3. Система логических выражений вида (П.5), заданная на факторном пространстве (подпространстве) событий, обладающая полнотой и непротиворечивостью, называется системой принятия решений (СПР).
Поясним важность свойств, указанных в определении.
То, что система функций f1, ..., fm является полной, означает, что любая точка факторного пространства событий входит в область задания хотя бы одной из этих функций. Непротиворечивость означает, что по каждой ситуации одна и только одна из этих функций принимает значение 1, приводящее к истинности соответствующего высказывания - решения. Однако отметим, что, в действительности, на основе смыслового содержания задачи, по каждой или некоторой ситуации может быть известно более одного правильного решения, приводящего к успешным действиям. В таком случае высказывания об этих решениях могут быть объединены операцией ИЛИ, что приводит к приведённому выше предположению о непротиворечивости.
Приведём теорему, которая даёт обоснование общего вида логического описания любой системы принятия решений – того вида, к которому на пути упрощения задачи рекомендуется приводить описание СПР для нейросетевой реализации.
Теорема 1.1. Любая логическая функция, входящая в состав описания системы принятия решений, может быть приведена к дизъюнкции конъюнкций высказываний о событиях.
Доказательство. Из основ математической логики (в частности, - теории булевых функций) известно, что каждая такая функция может быть представлена дизъюнктивной нормальной формой. Однако в ней, наряду с переменными, участвуют их отрицания. Ориентируясь на применение исчерпывающих множеств событий, воспользуемся (1.1) для выражения таких отрицаний. "Раскроем скобки", вновь выделив конъюнкции, объединённые операциями дизъюнкции. Упростим эти конъюнкции с помощью (1.2). Получим форму, объявленную в теореме. Теорема доказана.
Данная теорема объясняет, почему в последующих примерах преимущественно принимается именно объявленная форма описания СПР, или легко сводящаяся к ней, а отрицания событий не рассматриваются.
Пусть наша бабушка планирует занятия физкультурой и спортом во все времена года по времени дня: после завтрака, после обеда и после ужина. Объединяя высказывания по принципу "если - то" и пользуясь обозначениями на рис. 1.1, она формирует систему принятия решений, которой, не полагаясь на память, намерена строго следовать, добившись согласия администрации.
Система имеет вид:
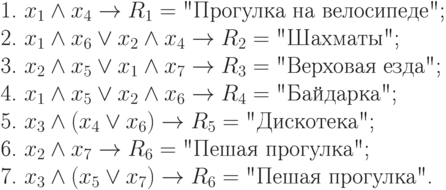 |
( 1.6) |
Планируя пешую прогулку, бабушка первоначально получила следующее выражение:
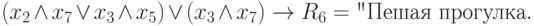
Однако выше не напрасно обращается внимание на целесообразность однократного вхождения переменных в подобное выражение. (Ведь далее, при переходе к функции активации нейрона, возможно неоднократное суммирование одних и тех же переменных.) Выражение, полученное первоначально, с помощью эквивалентных преобразований привести к такому виду не удаётся. Тогда бабушка решает разбить это выражение на два подобных, сформировав получение одного и того же решения ("размножив" решение) на основе двух условий. Это и послужило появлению в (П.6) двух выражений, определяющих одно решение R6.
Легко убедиться, что все возможные ситуации факторного пространства событий охвачены, что демонстрирует полную ясность действий бабушки.
Системы принятия решений могут образовывать сложные иерархические структуры. В этом случае необходимо, чтобы высказывания-решения R1, ..., Rm отображали события, образующие ИМС.
