Математическая логика событий и логические нейронные сети

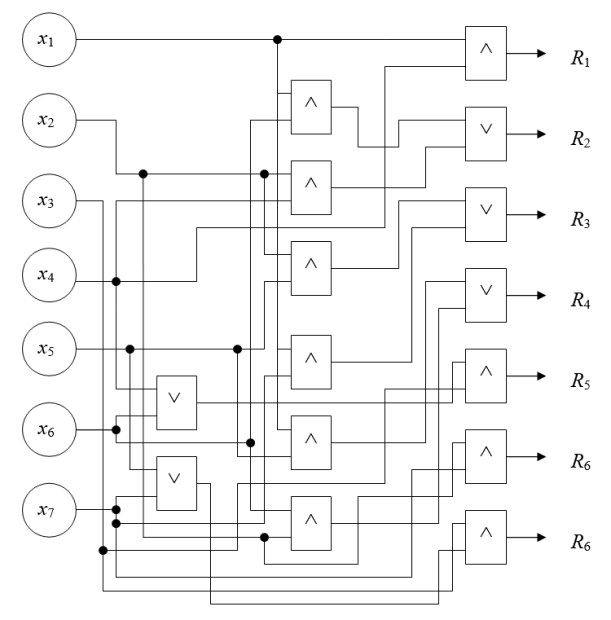
"Схемотехническое" представление системы принятия решений

Отобразим (c нарушением некоторых стандартов) схемотехнически бабушкину СПР, подобно электронной схеме (рис. П.4) с помощью конъюнкторов и дизъюнкторов. На вход будем подавать значения истинности переменных-высказываний (ситуации) так, чтобы на одном из выходов формировалась единица - значение истинности соответствующего решения. Задавать значение ситуаций следует корректно, чтобы соблюдать требования вхождения переменных в исчерпывающие множества событий.

увеличить изображение
Рис. 1.4. «Электронная» схема системы принятия решений

Реализовав эту схему на логических элементах, бабушка получит реальное средство подсказки: что она должна делать в данное время года и суток.

Например, бабушка хочет вспомнить, чем она должна заниматься летом после обеда. Она полагает x₂ = x₅ = 1 при нулевых значениях других переменных и запускает программу, моделирующую работу электронной схемы. На выходе R₃ формируется сигнал, соответствующий высказыванию "Верховая езда".

Электронная схема, имитирующая систему принятия решений, требует корректного задания исходной информации, т.е. корректной формулировки вопроса в соответствии со смыслом задачи. Одновременно должна существовать уверенность в получении единственного решения, в том числе предполагающего задание альтернативных вариантов, если это предусмотрено при построении СПР. В таком случае окончательный выбор альтернативы может быть предусмотрен при развитии системы, при анализе новых вводимых факторов. При некорректной формулировке вопроса возникнут коллизии, неоднозначные или неправильные выводы. Таким образом, СПР может отвечать только на те вопросы, на которые она настроена.

Достоверность высказываний о событиях

Говоря о высказываниях как о логических переменных, мы, несомненно, предполагаем наличие субъективного фактора: ведь это кто-то сказал. И мы говорим верному другу: "Я мало доверяю этому человеку, но он сказал ..., а дыма без огня не бывает".

Очевидно, недостаточно резких, кардинальных, взаимоисключающих, крайних суждений о высказываниях, подразделяющих их на истинные и ложные. Жизненный опыт говорит, что стопроцентной правды не бывает.

Таким образом, необходимо ввести понятие достоверность высказывания, которая идеально представляет вероятность того, что данное высказывание о свершении события истинно, т.е. представляющая его логическая переменная равна 1.

В этой оценке достоверности вновь практически преобладает субъективный фактор. Поэтому при построении экспертных систем применяется двойная оценка: оценка, данная экспертом по запросу, и вес самого эксперта. Здесь эффективно используется аппарат нечётких множеств.

Говоря о сложных высказываниях, отображаемых деревьями логических возможностей, тем более трудно судить о достоверности высказываний о событиях, особенно тех, которые отображаются концевыми вершинами.

Рассмотрим пример. Информатор сообщает Агенту о том, что видел своими глазами, как Марина передала Васе пачку денег. Напрягая богатый опыт, Агент рассуждает логически:

1. Насколько можно доверять Информатору, который три дня не брился и от которого дурно пахнет?
2. Мог ли находиться Информатор в это время в нужном месте, чтобы "видеть своими глазами"?
3. Насколько верно то, что в переданной пачке были деньги?
4. Можно ли оперативно воспользоваться существующими математическими методами оценки (например, аппаратом нечётких множеств) заодно учитывающими другие факторы, как, например, личные финансовые затруднения, или необходимые оценки следует выполнить интуитивно, "с потолка"?
5. Так какова же должна быть формулировка отчёта в Центр, для получения максимального вознаграждения за поимку взяточника?

Таким образом, видно, что оценка достоверности высказываний неизбежна, но представляет значительные практические трудности, тем более, - при требуемой оперативности этих оценок, столь важной в реальных системах управления и принятия решений.

Итак, на основе алгебры высказываний можно создавать электронные системы принятия решений: на входе задавать ситуацию, на выходе получать указание на правильную реакцию. Всё дело лишь в интерпретации предметной области - во вскрытии причинно-следственных связей, в исследовании личного или коллективного опыта, в изучении теории. Необходимы и схемотехнические навыки запоминания связей.

Однако смущают два обстоятельства:

1. Неопределённость исходной информации о ситуациях, исключающая точный ответ на вопрос о наличии или отсутствии события и делающая неправомерным использование исключительно булевых переменных. Высказывания не бывают истинными и ложными, как это предполагается в классической математической логике. Высказывания оцениваются своей достоверностью, которая принимает действительные значения на отрезке [0, 1], и подчиняется известным положениям теории вероятности.
2. Способность человека логично мыслить на неформальном уровне не реализуется с помощью конъюнкторов и дизъюнкторов в составе мозга. Именно вскрытие механизмов мышления, особенно того, которое мы называем рефлекторным, привлекает внимание исследователей. Необходимо искать механизмы мышления, оперирующие не с булевыми переменными, а с действительными, несущими смысл достоверности.

Пусть рассмотренные выше переменные-высказывания {x_i}, образующие факторное пространство, могут принимать значения достоверности .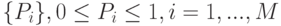

Так как факторное пространство формируется на основе исчерпывающих множеств событий, то внутри каждого такого множества выполняется известное правило нормировки: сумма достоверностей событий каждого такого множества равна единице.

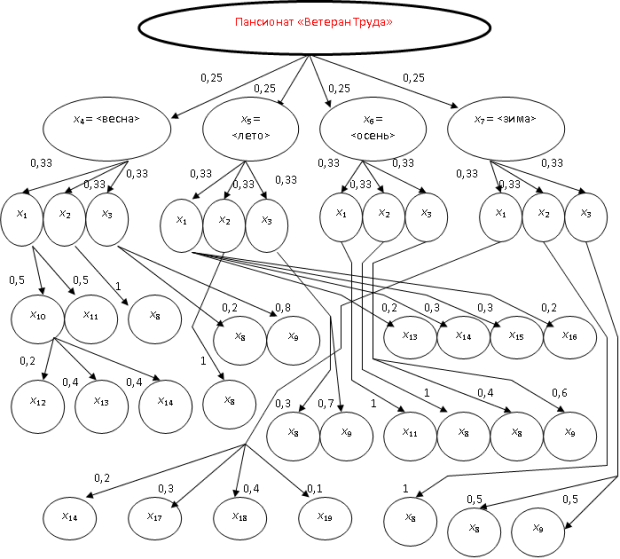
Перегруппируем события и дополним дерево логических возможностей, представленное на рисунке 1.1, указав на его ветвях (стрелках), в качестве весов этих ветвей, значения достоверности событий (рис. 1.5). Получим вероятностное дерево логических возможностей [21].

При организации ветвления в этом дереве также предполагаются все возможные альтернативы, т.е. исчерпывающие множества событий. Поэтому сумма вероятностей всех событий, отображаемых вершинами, которые связаны входящими стрелками, исходящими из некоторой вершины, равна единице.

увеличить изображение
Рис. 1.5. Вероятностное дерево логических возможностей

В отличие от дерева логических возможностей, вероятностное дерево явно отображает зависимость событий. События, зависимые от данного, отображаются более низкими уровнями ветвления. Такая зависимость определяется на уровне смыслового анализа факторного пространства.

Например, логично предположить, что формы труда, отдыха и спортивных развлечений зависят от времени года, затем, — от распорядка приёма пищи. Такая зависимость и отображается на рис. 1.5.

Тогда достоверность событий формируется с помощью условных вероятностей, зависящих от путей, по которым достигаются эти события. Поэтому на вероятностном дереве логических возможностей целесообразно повторять вершины одного смыслового содержания, в результате чего размножаются варианты ветвления, а дерево существенно разрастается. От совмещения путей страдает наглядность, и не более того.

Чтобы найти вероятность некоторого события b при условии свершения события а (событию а может соответствовать корневая вершина, тогда речь идёт о полной, а не условной вероятности), необходимо найти все пути, ведущие из a в b. По каждому пути необходимо перемножить все веса ветвей. Полученные по всем путям произведения необходимо сложить.

Пример 1. Найдём вероятность того, что отдыхающий весной и летом в произвольно выбранный момент времени совершает прогулку верхом:

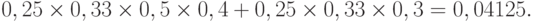
Пример 2. Найдём вероятность того, что в произвольно выбранный момент времени в течение года отдыхающий совершает прогулку верхом: