Нейросетевой метод ускоренного принятия решений операционной системой суперкомпьютера EPIC-архитектуры

...внутреннее стремление и постоянная тенденция капитала состоит в повышении производительности труда с целью удешевить товары, а посредством этого удешевить и самого рабочего

К. Маркс. Капитал

Выбор моделей логической нейронной сети

EPIC-архитектура (Explicitly Parallel Instruction Computing) компьютера, как правило, в составе многопроцессорной ВС, использует принцип программного управления каждым тактом машины [14, 22]. Суперкомпьютер такой архитектуры, используемый для управления в реальном времени, призван удовлетворять требованиям сверхвысокой производительности. Его основные особенности:

1. Распараллеливание на уровне выполнения команд в многофункциональном арифметическо-логическом устройстве (АЛУ), состоящем из конвейерных исполнительных устройств (ИУ).
2. Возможность параллельного ветвления при обработке конвейера команд в двух случаях: при обработке команд условного перехода и при выполнении конструкций вида if-then-else в составе арифметических операторов.

Чтобы снизить влияние эффекта остановки конвейера команд, в EPIC-архитектуре по предварительной команде за несколько тактов до ветвления запускается дополнительный конвейер. Конвейеры начинают работать в симулятивном режиме, не допуская "порчи" данных. Интенсивное ветвление выполняемой программы способно привести к лавинообразному запуску дополнительных, аппаратно поддержанных конвейеров. Очевидно, количество таких конвейеров ограничено.

Поэтому оптимально то программирование, при котором предпочтение отдаётся параллельному выполнению условных арифметических операторов (допускающих рекурсию), хотя это и приводит к избыточности оборудования, используемого при вычислениях. С помощью условных переходов следует поддерживать общую структуру программы, для обеспечения взаимодействия достаточно крупных работ. Следует также широко применять циклы типа "арифметическая прогрессия", где направление единственного перехода (выхода) предсказуемо заранее. Ведь целью оптимизации программирования суперкомпьютера является достижение минимального времени выполнения программы.

Таким образом, складывается культура программирования суперкомпьютера EPIC-архитектуры.

Управление ресурсами суперкомпьютера и многопроцессорной ВС, представляющее основу функций ОС, в общем случае сводится к анализу некоторой ситуации - вектора измеренных или ожидаемых характеристик устройств или вычислительного процесса и к выработке решений по планированию дальнейшей эксплуатации вычислительных ресурсов, по управлению вычислительным процессом, по устранению неисправностей, по визуализации и т.д.

В суперкомпьютерах широко используются модули ассоциативной памяти (АП) для кодирования и быстрой выборки отношений "причина - следствие". АП эффективна при организации виртуальной памяти, при обработке "глобалов", для хранения меток перехода, в системах контроля, в арбитрах коммутаторов, при решении конфликтов многоканального обмена и пр. Однако применение АП ограничено из-за существенных недостатков: 1) они не работают по нечётким данным; 2) они не используют взвешенные данные.

Любая система принятия решений (СПР) является универсальной и полной, если она предполагает нечёткие исходные данные и способна в процессе модернизации и развития учитывать различные факторы, и даже их значения, со своим весом.

Можно выделить ряд задач, решаемых ОС и являющихся основой создания многих СПР:

1. Принятие решения о реконфигурации вычислительной системы на основе вектора состояния её средств.
2. Выбор оптимальной стратегии обслуживания очереди "к процессору" на основе текущего вектора характеристик этой очереди.
3. Выбор оптимальной стратегии управления многоканальным обслуживанием многопользовательского режима на основе -характеристик, приоритетного ряда и других показателей потоков заявок.
4. Обработка результатов контроля и диагностики вычислительных средств.
5. Разрешение конфликта при обмене по внутренним магистралям и в компьютерной сети в целом.
6. Адаптивный выбор пошагового смещения информационных пакетов в компьютерной сети.
7. Принятие решений по статистической оценке динамики загрузки модулей.
8. Экспертное управление надёжностью средств системы, включающей разнородные устройства и объекты, оперирующих объектами разных типов, измерений и т.д.
9. Выбор оптимальной стратегии распараллеливания на основе характеристик потока заданий и данных и многие другие задачи.

Все указанные задачи, при попытке найти точное оптимальное решение, относятся к классу трудно формализуемых задач большой сложности, опирающихся на перебор. Практически используются эвристические методы решения, в основу которых берутся достаточно нетрудоёмкие решающие правила. С конца 70-х - начала 80-х годов особые надежды стали возлагать на применение методов искусственного интеллекта (ИИ) и, прежде всего, на нейросетевые технологии. В значительной степени это было связано с предполагаемой возможностью получить "быстрые" алгоритмы решения некоторых задач. Появилось понятие "эквивалентной" производительности при решении таких задач по сравнению с производительностью реальной.

Однако полную универсальность нейросетевые технологии обрели с построением и развитием логических нейронных сетей (ЛНС). ЛНС - универсальный аппарат моделирования ассоциативного мышления человека, определивший класс численных методов решения информационно-логических задач и задач управления.

В применении к ОС целесообразно выделить два основных типа ЛНС, отличающихся организацией рецепторного слоя.

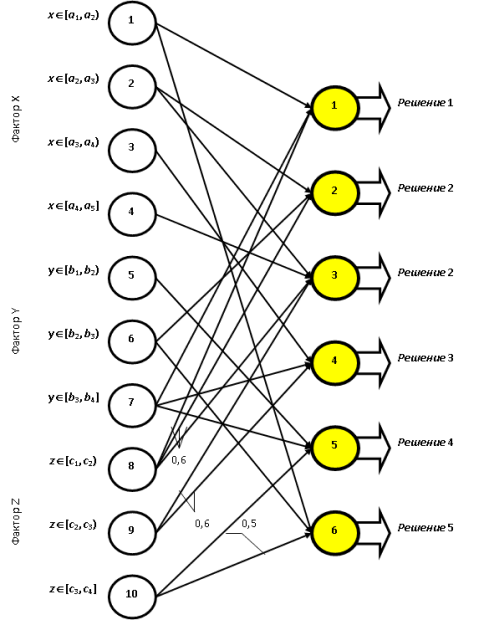
На рис. 16.1 дан пример ЛНС, где за рецепторами закреплены интервалы (закрытые или полузакрытые) значений факторов. Присутствуют некоторые веса связей. Если вес на стрелке не указан, то он равен единице.

Практически, веса, отличные от единичных, становятся известны в результате длительной эксплуатации СПР. Ведь это - вопрос о том, какие факторы и насколько влияют на достоверность результата применения ЛНС, и целесообразно ли это учитывать. На начальном этапе разработки СПР, как правило, все веса принимаются равными единице, если нет очевидных ограничений.

увеличить изображение
Рис. 16.1. Закрепление рецепторов за интервалами значений факторов

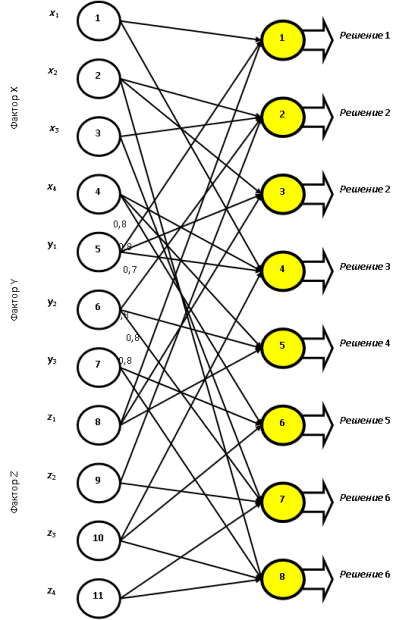
Второй тип ЛНС, отражающий результат экспериментальных исследований, моделирования или экспертных оценок, представлен на рис. 16.2.

увеличить изображение
Рис. 16.2. Логическая нейронная сеть, составленная на основе экспериментов, моделирования или экспертных оценок

Введение весов синапсических связей приводит к применению функции активации нейрона:

( 16.1)

Здесь v индексирует номера рецепторов, связанных с k-м нейроном.

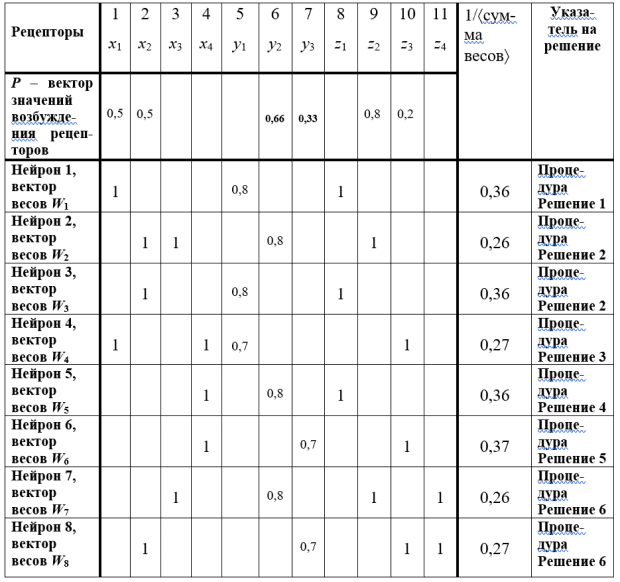
Для компьютерной обработки однослойная ЛНС на рис. 16.2 представляется матрицей связей (табл. 16.1).

Табличное представление делает весьма удобными модификацию и развитие ЛНС в процессе обучения: добавление новых факторов или их значений, изменение связей, весов, уточнение решений, текст или процедуры которых хранятся отдельно. По таблице же находится указатель на принимаемое решение по максимально возбудившемуся нейрону.

увеличить изображение
Табл. 16.1. Матрица связей

Возбуждение рецепторов

1. Если значения факторов заданы интервалами вида [d, e), значение р (индекс опущен) величины возбуждения соответствующего рецептора, при анализе измеренного или предполагаемого значения g, находится как результат счёта логического арифметического оператора:

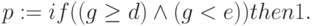( 16.2)

Если интервал имеет вид [d, e], знак "<" в (16.2) меняется на .

2. Если интервал принадлежности испытываемого значения фактора определён нечётко, "единица" делится на количество предполагаемых интервалов принадлежности, что определяет значение р для каждого такого интервала. Однако такие действия характерны при требовании полной автоматизации. Реально же значения р возбуждения рецепторов, закреплённых за предполагаемыми интервалами, следует задавать в диалоговом режиме на основе экспертных оценок или предположений оператора-пользователя.

3. Если измеренное или предполагаемое численное значение g является промежуточным, не совпадающим ни с каким значением, которому соответствует рецептор, находятся два ближайших (меньшее d и большее e) значения фактора, за которыми закреплены рецепторы ("ближайшие рецепторы"), и "единица" распределяется обратно пропорционально "расстоянию" до этих рецепторов:

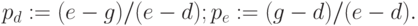( 16.3)

Предлагается параллельный счёт значений p_d и p_e (ведь p_e = 1 - p_d). Рекомендуется значения вида 1/(e - d) рассчитывать заранее и хранить до модификации ЛНС. Счёт обратной величины на этапе формирования (обучения) ЛНС предпочтителен, так как конвейер деления значительно "длиннее" конвейера умножения, оперативно используемого в рабочем режиме.

4. Если значение g находится вне диапазона значений, представленных рецепторами, то есть, для него можно указать лишь одно значение d или e, за которым закреплён рецептор, то вместо разности (e - d), используемой в (16.3), можно взять среднее "расстояние" между рецепторами сети и выполнить один из операторов:

( 16.4)

5. Если фактор предполагает нечисловые значения, возбуждение рецепторов задаёт пользователь в диалоговом режиме.

Например, пусть в ЛНС СПР, обслуживающей охотников (рис. 16.1), рецептор х₁ фактора Х соответствует высказыванию "рысь", а рецептор х₂ - высказыванию "дикая кошка". Никто из охотников не смог с полной уверенностью определить, следы принадлежат рыси или дикой кошке? Они полагают значение возбуждения рецепторов 1 и 2 равными 0,5 (р₁ = р₂ = 0,5). Пусть фактор _Y отражает количество охотников. Их оказалось шесть человек. Рецептора, закреплённого за таким количеством, нет. Однако "ближайшими" рецепторами являются y₂, отвечающий за 5 человек, и y₃, отвечающий за 8 человек. Возбуждаем эти рецепторы распределением "единицы" обратно пропорционально "расстоянию" исследуемого значения 6 до них: р₆ = 0,66, р₇ = 0,33. Пусть на основе подобных рассуждений заполнены клетки фактора Z в табл. 1: р₉ = 0,8, р₁₀ = 0,2.

На больших ЛНС с помощью рецепторов можно имитировать любой закон распределения вероятностей, в том числе, нормальный.

Таким образом, ЛНС работает с нечёткими данными, что составляет основной смысл ассоциативного мышления.

Схема поиска решения

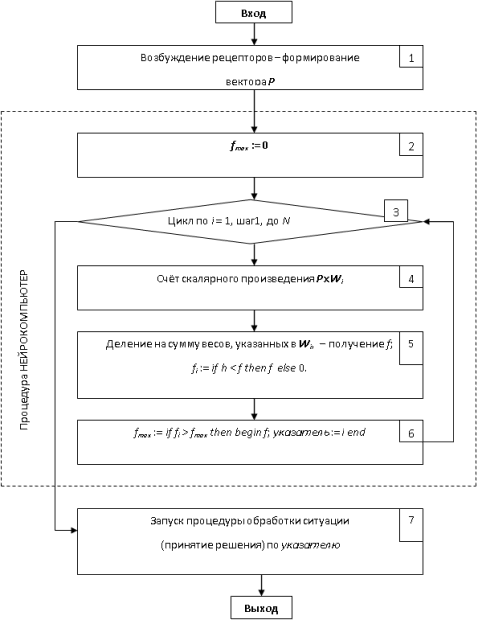
Общая схема нахождения оптимального решения с помощью ЛНС показана на рис. 16.3. В процедуру НЕЙРОКОМПЬЮТЕР выделены блоки, которые реализуют собственно нейрокомпьютер. Процедура может быть использована в различных приложениях, не обязательно только в составе ОС.

увеличить изображение
Рис. 16.3. Схема принятия решения, включающая процедуру НЕЙРОКОМПЬЮТЕР

Легко видеть, что самой трудоёмкой операцией здесь является нахождение скалярного произведения вектора значений возбуждения рецепторов и вектора, образуемого строкой весов связей нейрона. Затем значение найденного произведения умножается на соответствующий элемент последнего столбца матрицы связей и сравнивается с порогом h для получения неотрицательного значения функции активации. Попутно фиксируется нейрон с максимальным значением возбуждения, указывающий на рекомендуемое или автоматически выполняемое решение - по завершении анализа всех нейронов.

Порог h выбирается экспериментально так, чтобы сократить анализ лишних, заведомо отвергнутых вариантов решения.

Если величина возбуждения ни одного нейрона не превысила порог, следует, изучив ситуацию, либо повысить порог, либо "научить" ЛНС новой для неё ситуации.

Таким образом, с помощью ЛНС производится "голосование" в пользу "наиболее возбудившегося" решения. Однако если находятся численные значения, например, значение рейтинга объекта, то на основе величины возбуждения нескольких нейронов, преодолевших порог, может быть найдено среднее значение искомой величины по той же формуле, что лежит в основе функции активации. Тогда величины возбуждения нейронов используются в качестве весов решений, на которые эти нейроны указывают.

Например, пусть в некоторой, здесь не приведённой ЛНС значение возбуждения нейрона 1, указывающего на ответ "необходимо 40 человек", равно 0,5. Значение возбуждения нейрона 2, указывающего на ответ "необходимо 50 человек", равно 0,8, а значение возбуждения нейрона 3, указывающее на 60 человек, равно 0,6. Возбуждение других нейронов нулевое. Тогда среднее количество людей, рекомендуемых ЛНС, составляет:

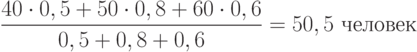
Пусть обосновано значение h = 0,4. По рис. 16.2 и по табл. 16.1 рассчитаем значения возбуждения всех нейронов. Оно оказалось равным 0, кроме значения f₂ = 0,5. Как максимальное возбуждение нейронов, это значение указывает на Решение 2.

Оптимизация скалярного умножения векторов при счёте значения функции активации

Рассмотрим возможность оптимизации (по времени выполнения) скалярного умножения векторов P и W (индекс опускаем), отражённого в блоке 4 на рис. 16.3. Оптимизация достигается применением двух методов:

1. "Зацеплением" двух векторных конвейеров умножения с векторным конвейером сложения;
2. Сложением всех результатов умножения с помощью операции "свёртки" массива [15] по схеме "двоичного дерева", что обеспечивает непрерываемый счёт на векторном конвейере сложения с окончательным получением суммы в корневой ячейке дерева.

Рис. 16.4. Схема двоично-древесной обработки буфера

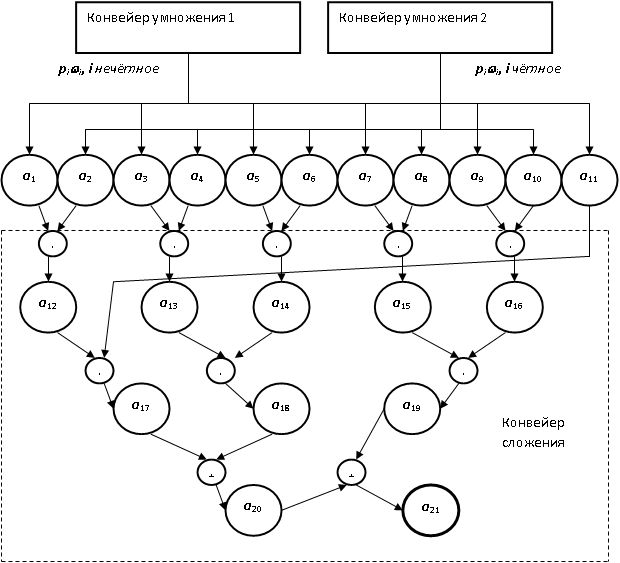
Схема счёта по табл. 16.1 показана на рис. 16.4.

Пусть даны два вектора P = {p₁, ..., p₁₁} и . Тогда один конвейер умножения обрабатывает нечётные пары элементов, а второй - чётные пары элементов. (Обычно используется индексация с нуля; индексация с единицы более наглядно отождествляется с порядком действий.) Рабочий массив А содержит 21 регистр, А = {a₁, ..., a₂₁} ((2N - 1) регистров). Конвейеры умножения заполняют первые N регистров. Конвейер сложения запускается тотчас по получении первой пары произведений и синхронно с умножением выполняет сложение по двоично-древесной схеме, как показано на рисунке.

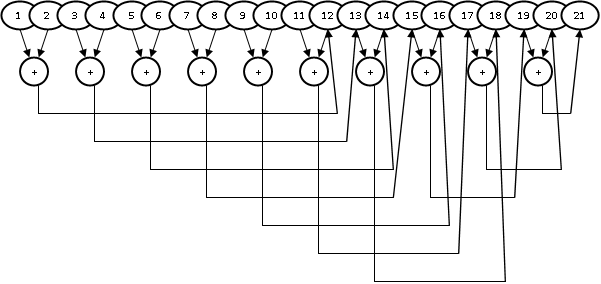
Схема регулярных действий конвейера сложения при обработке рабочего массива регистров показана на рис. 16.5. Для краткости используются только индексы (номера) регистров.

Рис. 16.5. Схема обработки буфера векторным конвейером сложения

При отсутствии в АЛУ векторных конвейеров со специальной аппаратной поддержкой, схеме этой обработки соответствует цикл типа "арифметическая прогрессия":

i := 1; для j = 1 до N - 1 выполнять: begin a_N+j := a_i + a_i+1; i := i + 2; end.

(Производя "набросок" программы, мы не следуем канонам какого-либо языка.)

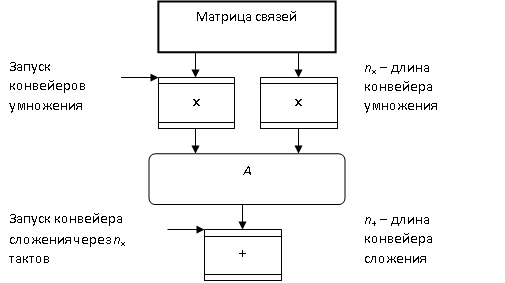
На рис. 16.6 показана синхронная работа векторных конвейеров при управлении каждым тактом машины.

Рис. 16.6. Последовательность запуска векторных конвейеров

Распараллеливание скалярного умножения векторов

Если АЛУ содержит достаточное количество конвейерных ИУ, возможности распараллеливания могут быть расширены. Это относится к скалярному умножению векторов, как основной операции нейрокомпьютера.

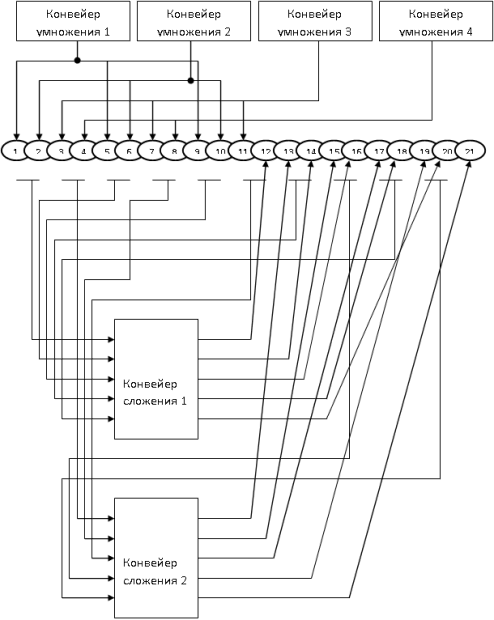
На рис. 16.7 показано использование четырёх векторных конвейеров умножения и двух векторных конвейеров сложения для ранее рассмотренной нейросети.

В представленных случаях управления в каждом такте синхронизация использования данных не требуется, если: 1) количество рецепторов в нейронной сети не менее чем вдвое превышает количество уровней конвейера сложения; 2) в качестве буфера не используется оперативная память (ОП). В первом случае возникает опасность считывания данных до их формирования. Во втором случае ОП, вследствие конфликтов при обращении, вносит элемент нестабильности в режим управления каждым тактом компьютера.

увеличить изображение
Рис. 16.7. "Зацепление" четырёх конвейеров умножения с двумя конвейерами сложения

Большой объём ЛНС может привести к активному использованию ОП, если объёма сверхоперативного запоминающего устройства (СОЗУ) станет недостаточно. Тогда в обоих случаях синхронизация может быть выполнена с помощью закрытия адресов по считыванию, которые открываются по окончании записи по ним. В процессорах "Эльбрус" такой синхронизации служат биты значимости [23].

Рекомендация. Анализ многих примеров показывает, что вектора, участвующие в операции скалярного умножения, являются сильно разреженными, т.е. содержащими много нулевых элементов. Ведь на каждый нейрон подаётся возбуждение весьма малого количества рецепторов по сравнению с их общим числом. Целесообразно в дополнение матрицы связи указывать для каждого нейрона только те рецепторы (и задавать значения их возбуждения), с которыми он связан с учётом весов. Тогда в скалярном умножении, являющемся главной составляющей счёта функции активации, будут участвовать вектора минимальной длины. Время работы конвейеров будет минимальным.

Краткие итоги

1. Независимо от типа логической нейронной сети, основой функции активации является скалярное умножение векторов, требующее минимизации времени выполнения.
2. Операция зацепления векторов является основой такой минимизации.
3. Практически наблюдаемая разреженность векторов, обусловленная тем, что каждый нейрон связан со сравнительно небольшим количеством рецепторов, требует задания дополнительной информации о действительных связях каждого нейрона. Это способствует достижению минимального времени счёта функции активации.

Вопросы

1. К каким двум типам сводятся логические нейронные сети?
2. Что представляет собой общая часть всех возможных функций активации, трудоёмкость выполнения которой представляет основную проблему нейрокомпьютера?
3. Как с помощью зацепления конвейеров умножения и сложения минимизировать время выполнения операции скалярного умножения векторов?
4. Какую дополнительную информацию следует задать, чтобы добиться минимального времени счёта значения функции активации?