Основы математической логики
Изучать философию нужно, когда философия вам не нужна. Когда вы догадываетесь, что стулья в вашей гостиной и Млечный путь связаны между собою, и более тесным образом, чем причины и следствия, чем вы сами с вашими родственниками. И что общее у созвездий со стульями – бесчувственность, бесчеловечность.
Иосиф Бродский. Выступление в Сорбонне
Булева алгебра
Да, Поэт прав: всякая формализация основ нашей жизни - мышления, призвана утвердить на абстрактном уровне бесчувственность, бесчеловечность. Но это оправдано, если целью наших исследований является не паразитическое применение методов человеческого интеллекта во благо личности, а его развитие.
Казалось бы, после Лекции 1 возвращаться к основам математической логики нет смысла. Но ведь там был приведён только материал, позволивший построить новую теорию - математическую логику событий. Были ли при этом исчерпаны все построения, позволяющие в широком плане моделировать искусственный интеллект? Очевидно, нет. Кроме того, перед вами не монография, а учебное пособие, где в методическом плане разделы должны быть достаточно автономны и содержать допустимое повторение основ, в разных вариантах складывающихся в систему. В то же время, излишнее теоретизирование недопустимо.
Джордж Буль (1815 - 1864) - английский математик и логик. В статье "Математический анализ логики" (1847) им впервые были высказаны идеи применения символического метода к логике. Буль не считал логику разделом математики, но находил глубокую аналогию между символическим методом алгебры и символическим методом представления логических форм и силлогизмов. Он показал, что логические конструкции в такой символике можно решать с помощью аналогов операций алгебры. Таким образом, Д. Буль ввёл базовые операции математической логики и заложил основы булевых функций.
Булевой алгеброй будем называть множество конечноместных (с конечным числом переменных) булевых функций, рассматриваемое вместе с заданными на нём операциями отрицания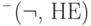 
, дизъюнкции 
и конъюнкции 
.
В общем случае булевы функции следует определять рекурсивно. Это следует из того, что аргументы могут быть или рассматриваться как булевы функции.
При композиции или рекомпозиции структура булевых функций выражается с помощью скобок.
Булевы функции и их композиции образуют формулы F. Одной из основных задач булевой алгебры является установление тождественных соотношений вида F1 = F2. Формулы являются тождественными, если при любом наборе значений переменных ИСТИНА (1) или ЛОЖЬ (0), их значения истинности совпадают.
Соблюдается ранжирование операций: первым при прочих равных условиях выполняется отрицание, затем конъюнкции, затем дизъюнкции. При необходимости выполнения действий в ином порядке употребляются скобки.
Для булевой алгебры известен базовый набор тождественных соотношений, определяющий правила эквивалентных преобразований для установления тождественности формул или для обслуживания технологических требований.
(В Лекции 1 утверждается, что любая система распознавания, управления или принятия решений, описанная в терминах булевой алгебры, сводится к построению однослойной логической нейронной сети; это сокращает трудоёмкость обработки, повышает достоверность выводов, и делает даже нецелесообразным изучение структурированных логических нейронных сетей.)
Подчеркнём ещё раз, что тождественность булевых функций устанавливается с помощью таблицы, где по каждому набору значений переменных рассчитываются значения функций. Должно соблюдаться полное соответствие.
Рассматривая буквы латинского алфавита в качестве независимых переменных, повторим здесь базовый набор тождественных соотношений, приведённый в Лекции 1:
Закон коммутативности:
 |
( 3.1) |
 |
( 3.2) |
Закон ассоциативности:
 |
( 3.3) |
 |
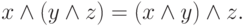( 3.4) |
Закон дистрибутивности:
 |
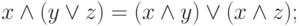( 3.5) |
 |
( 3.6) |
Закон де Моргана:
 |
( 3.7) |
 |
( 3.8) |
Закон идемпотенции:
 |
( 3.9) |
 |
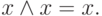( 3.10) |
Закон поглощения:
 |
( 3.11) |
 |
( 3.12) |
Закон склеивания:
 |
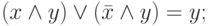( 3.13) |
 |
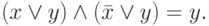( 3.14) |
Операция переменной с инверсией:
 |
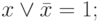( 3.15) |
 |
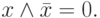( 3.16) |
Операция с константами:
 |
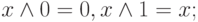( 3.17) |
 |
( 3.18) |
Двойное отрицание:
 |
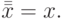( 3.19) |
Применяя эквивалентные преобразования на основе приведённого базового набора, можно аналитически упростить формулу, сделать её короче, нагляднее. Это можно делать, например, раскрывая или вводя скобки, выделяя или формируя конструкции, попадающие под действия перечисленных выше законов и операций.
Например,
В данном случае функция F(x1, x2) нам задана. А можно ли сформировать вид этой функции, задав с помощью таблицы её значения для всех возможных наборов значений переменных?
Да, табличный метод задания булевой функции породил полную, стандартизованную и легко реализуемую, предельно "прозрачную" форму - совершенную дизъюнктивную нормальную форму (СДНФ).
Пусть задано табличное представление некоторой булевой функции четырёх переменных (табл. 3.1)
| x1 | x2 | x3 | x4 | F |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Запишем в общем виде, основанном не на строгом доказательстве, а на догадке, СДНФ для четырёх переменных:
 |
( 3.20) |
После подстановки заданных значений функции F получим:
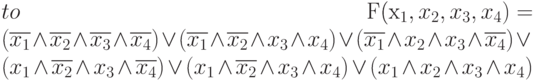
Не будем искать дальнейших упрощений, так как полученный вид функции достаточно регулярен и, несмотря на кажущуюся избыточность, достаточно легко реализуется схемотехнически самой короткой логической цепочкой. Необходимо на первом уровне выполнить инверсию (отрицание), на втором уровне - выполнить конъюнкции, а на третьем - дизъюнкцию. Это особенно важно при построении быстродействующих устройств суперкомпьютера и, как оказалось (см. Лекцию 1), - при построении однослойных логических нейронных сетей.
Как видим формула (3.20) получилась весьма длинной, и это всего лишь для четырёх булевых переменных! Можно ли записать короче для любого количества n переменных?
Пусть задан вектор X = {x0, x1, ..., xn-1}, где xj, j = 0, ..., n-1, - булевы переменные. Введём понятие индексной маски вектора ИМВ. Она представляет собой двоичный код длины n, принимающий 2n значений индекса i от равенства нулю до равенства единице всех разрядов. Пусть при данном применении единичные разряды ИМВ, образующие двоичное значение индекса i, указывают на те булевы переменные, которые используются в выражении (3.20) без знака отрицания. Такую i-ю выборку вектора Х обозначим ХИМВ=i. Функцию F от неё обозначим F(ХИМВ=i), а соответствующую ей конъюнкцию булевых переменных, с учётом того, что часть их фигурирует со знаком отрицания, обозначим
Тогда всю формулу СДНФ можно записать:
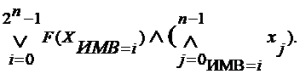(3.21)
В рассмотренном выше примере для n = 4 не зря каждая следующая комбинация выбиралась по строкам таблицы условным сложением с единицей некоторой подразумеваемой маски. Эти комбинации образовали счётное множество с индексом i, пробегающим от нуля до единиц по всем четырём разрядам. Частный вид подтверждает общую формулу (3.21):
(3.22)
В данном случае надо помнить о специальном назначении маски, метящей булевы переменные, используемые без знака отрицания.
Маски векторов используются программистами весьма часто: для альтернативного выполнения векторных операций, для маскирования прерывания, для маскирования направлений обмена и пр.
Из СДНФ легко выводится СКНФ - совершенная конъюнктивная нормальная форма, представляющая собой "конъюнкцию дизъюнкций". Поскольку она практически не применяется, мы её рассматривать не будем.
Отметим, что табличная запись булевых функций не только достаточна, но практически всегда используется разработчиками цифровых электронных устройств. Более того, сложилась практика использования ассоциативной памяти (АП) для построения многих устройств компьютера, таких как: дешифратор, КЭШ в сверхоперативной памяти, механизм перевода математических адресов в физические, устройство хранения и выборки глобальных данных, арбитры коммутаторов и др.
Табличная запись значений одной или более булевых функций производится в строках - регистрах АП, разбитых на две части: в левой части указан набор значений переменных, а в правой - вектор значений булевых функций. В результате одновременного сравнения кода возникшей ситуации со всеми наборами переменных, мгновенно производится выбор вектора значений выходов устройства. То есть, устройство со многими входами и многими выходами записывается и работает с помощью модуля ассоциативной памяти, реализующего систему булевых функций.
Так решаются задачи обеспечения высокого быстродействия, стандартизации и унификации.
Требования стандартизации и унификации элементной базы и функциональных устройств электронной техники, в том числе нейросетевых технологий, выдвигает научную задачу синтеза сложных булевых функций на основе более простых базовых, стандартных. В этом случае функция с меньшим количеством булевых переменных "погружается" в более сложную булеву функцию, где добавляются новые переменные.
Существует теорема разложения, которую проиллюстрируем конкретным, легко обобщаемым примером:
 |
( 3.23) |