Основы математической логики
Основы исчисления предикатов
Особенностью исчисления предикатов является наличие предметных переменных, пробегающих конечную или бесконечную область значений, называемую предметной областью. Отдельные значения этой области называются предметами или объектами.
Предикатом называют функцию предметных переменных P(x1, x2, ..., xn), представляющую собой переменное высказывание, истинность или ложность которого определяется наборами значений переменных x1, x2, ..., xn.
Если предикат Р не является тождественно истинным или тождественно ложным, то на одних наборах значений предметных переменных он принимает значение ИСТИНА (1), а на других - значение ЛОЖЬ (0).
Какова цель построения исчисления предикатов?
При построении теоретических основ логических нейронных сетей - математической логики событий - мы исходили из высказываний, вкладывая в них конкретный смысл на основе факторного пространства событий. Это пространство и отражало предметную область. Значит, до перехода к нечётким данным, мы пользовались расширением исчисления высказываний в сферу исчисления предикатов!
Действительно, ведь необходимо придать формальному языку логического вывода "человеческий", объектовый и событийный смысл. Чтобы видеть и подразумевать предметы и объекты, свойства и обстоятельства, о которых что-то говорится. Чтобы не были истинными такого рода высказывания, как "из-за того, что у льва когти, снег белый". Чтобы лев и снег действенно участвовали в поиске истины.
Введение понятия предметной области сразу же влечёт применение теоретико-множественного аппарата, подобно тому, что привлекался в силлогистике.
Мы подробно не останавливались и не будем останавливаться на анализе преемственности учения о силлогистике и о современной математической логике, но готовы высказаться в защиту тезиса о том, что "всё новое - хорошо забытое старое". Именно поэтому мы ввели в курс об искусственном интеллекте силлогистику Аристотеля.
Например, высказывание "четыре больше двух" в исчислении высказываний является неразложимым. Если же ввести предикат P(x, y) на множестве целых неотрицательных чисел в качестве предметной области, который является истинным тогда и только тогда, когда  , то приведённое высказывание запишется в форме Р(4, 2), которая даёт ясное представление о внутренней структуре высказывания.
, то приведённое высказывание запишется в форме Р(4, 2), которая даёт ясное представление о внутренней структуре высказывания.
Наличие предметных переменных позволяет ввести квантор общности \forall x и квантор существования  .
.
Выражение 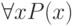 - условное обозначение высказывания "для всех х предикат Р(x) является истинным"; выражение
- условное обозначение высказывания "для всех х предикат Р(x) является истинным"; выражение 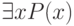 - условное обозначение высказывания "существует x, для которого предикат Р является истинным".
- условное обозначение высказывания "существует x, для которого предикат Р является истинным".
В теории доказательств эти кванторы связаны между собой:
 |
( 3.46) |
Например, высказывание "все солдаты карантинной роты стригутся наголо" в случае отрицания звучит: "не все солдаты карантинной роты стригутся наголо". Это, в свою очередь, может быть сформулировано: "существует солдат карантинной роты, постриженный не наголо".
Пусть Р(x) - функция "x стрижётся наголо". Тогда вышесказанная трансформация может быть изображена цепочкой:

Если предметная область состоит из конечного числа объектов x1, x2, ..., xk, подобных солдатам, то выражение 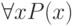 сводится к конъюнкции
сводится к конъюнкции 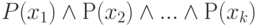 , а выражение
, а выражение  - к дизъюнкции
- к дизъюнкции 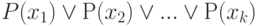 . В случае бесконечной предметной области подобное сведение оказывается невозможным, неконструктивной.
. В случае бесконечной предметной области подобное сведение оказывается невозможным, неконструктивной.
Возьмём более сложный пример. Вспомним определение непрерывности функции f(x) в точке x0: "Функция f(x) непрерывна в точке x0, если для любого  существует
существует 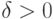 , что если
, что если  , то
, то  ". Сокращённо можно записать:
". Сокращённо можно записать:
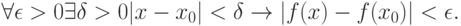 |
( 3.47) |
В случае нарушения непрерывности функции мы говорим: "не для всякого  существует
существует 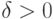 , что если
, что если  , то
, то  ". Или: "существует
". Или: "существует  , что для любого
, что для любого 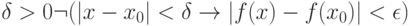 ". Последний предикат можно записать формально:
". Последний предикат можно записать формально:
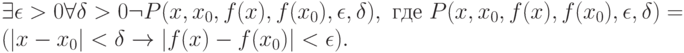 |
( 3.48) |
В выражениях 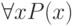 и
и  переменная x оказывается связанной соответствующим квантором, в отличие от свободных переменных. В формулах (3.47) и (3.48) переменные
переменная x оказывается связанной соответствующим квантором, в отличие от свободных переменных. В формулах (3.47) и (3.48) переменные 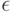 и
и 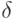 связанные, а переменные x, x0, f(x), f(x0) - свободные.
связанные, а переменные x, x0, f(x), f(x0) - свободные.
Обычно используют узкое исчисление предикатов, которое разрешает связывать с помощью кванторов лишь предметные переменные. Входящие в формулу предикаты предполагаются при этом неизменными. В так называемом расширенном исчислении предикатов употребляются переменные предикаты и предикатные кванторы.
Как и в случае исчисления высказываний, при построении исчисления предикатов недостаточно указать лишь способ записи формул. Необходимо задать правила преобразования формул, выражаемые аксиомами.
В число аксиом исчисления предикатов включаются все 11 аксиом исчисления высказываний, (3.25) - (3.35).
Кроме них, вводятся четыре специфических постулата, которым присвоим номера от 12 до 15:
12.
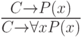 |
( 3.49) |
13.
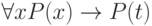 |
( 3.50) |
14.
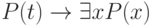 |
( 3.51) |
15.
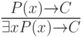 |
( 3.52) |
С помощью указанных аксиом - постулатов можно производить формальный вывод новых эквивалентных формул совершенно таким же способом, как и в исчислении высказываний.
Заметим, что выражения P(x) и P(t) в аксиомах 12 - 15 должны пониматься не только как элементарные одноместные предикаты, но и как произвольные формулы исчисления предикатов, содержащие буквы x и t в качестве свободных переменных.
При всех подстановках подразумевается, что свободные и связанные переменные в формулах, получаемых в результате подстановок, должны обозначаться различными буквами, как в (3.50) и (3.51). Такое условие позволяет избежать так называемой коллизии переменных, вызывающей непредвиденное связывание переменных, которые должны были бы остаться свободными.
При условии принятия мер во избежание коллизии переменных, в исчисление предикатов переносятся все результаты выводимости одних формул из других. Остаётся справедливой и теорема дедукции.
В частности, если формула  выводима в исчислении высказываний из формулы
выводима в исчислении высказываний из формулы  , то формула
, то формула 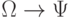 , при условии принятия мер против коллизии переменных, будет выводимой и в исчислении предикатов.
, при условии принятия мер против коллизии переменных, будет выводимой и в исчислении предикатов.
Из аксиом 12 - 15 легко образуются следующие правила выводимости:
Введение квантора общности (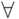 -введение)
-введение)
 |
( 3.53) |
(Значок переменной x, который пишется над символом выводимости 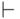 , означает, что соответствующая переменная варьируется, превращаясь из свободной в связанную. Тогда свободные переменные, не варьирующиеся в процессе вывода, принято называть фиксированными.)
, означает, что соответствующая переменная варьируется, превращаясь из свободной в связанную. Тогда свободные переменные, не варьирующиеся в процессе вывода, принято называть фиксированными.)
Введение квантора существования ( -введение)
-введение)
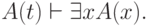 |
( 3.54) |
Удаление квантора общности (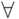 -удаление)
-удаление)
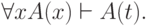 |
( 3.55) |
Удаление квантора существования по С.К. Клини:
 |
( 3.56) |
(Напоминаем, что  - произвольная конечная совокупность формул.)
- произвольная конечная совокупность формул.)
Если имеет место выводимость 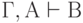 , причём, в процессе вывода свободные переменные, входящие в формулу А, остаются фиксированными, то имеет место сводимость
, причём, в процессе вывода свободные переменные, входящие в формулу А, остаются фиксированными, то имеет место сводимость 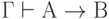 .
.
Используя символ эквивалентности 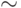 в том же смысле, что и в исчислении высказываний, и обозначая буквой А любую формулу, не содержащую свободной переменной х, можно легко вывести следующие соотношения:
в том же смысле, что и в исчислении высказываний, и обозначая буквой А любую формулу, не содержащую свободной переменной х, можно легко вывести следующие соотношения:
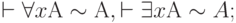 |
( 3.57) |
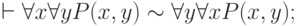 |
( 3.58) |
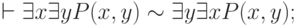 |
( 3.59) |
 |
( 3.60) |
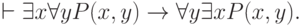 |
( 3.61) |
Правила (3.58) и (3.59) показывают возможность изменения порядка применения одноимённых кванторов. Для разноимённых кванторов смена их порядка в соотношении (3.61) не имеет места. Теоретико-множественный анализ соотношения  , двойственного (3.61), обнаруживает примеры его абсурдности. ("Отрицательный вывод не доказывается, а показывается" - важное правило теории доказательства; см. пример о непрерывности функции.)
, двойственного (3.61), обнаруживает примеры его абсурдности. ("Отрицательный вывод не доказывается, а показывается" - важное правило теории доказательства; см. пример о непрерывности функции.)
Содержательная непротиворечивость исчисления предикатов, как и исчисления высказываний, понимается в том смысле, что выводимыми в этом исчислении могут быть лишь тождественно истинные формулы, т.е. такие формулы, которые остаются истинными для любой предметной области и для любой конкретной интерпретации входящих в них предикатов. Здесь кроется некоторая неконструктивность подхода, связанная с неявно предполагающейся возможностью перебора всех значений предметных переменных при определении тождественной истинности. В случае бесконечной предметной области это требует бесконечного числа шагов. Поэтому широко привлекается теоретико-множественный подход, основанный на смысловом анализе как предметной области, так и заданных на ней предикатов.
Подобным путём устанавливается и формальная непротиворечивость исчисления предикатов, как невозможность вывести в этом исчислении некоторую формулу вместе с её отрицанием.
В случае конечных предметных областей вопрос о содержательной полноте исчисления предикатов сводится к соответствующему вопросу для исчисления высказываний и потому решается конструктивно.
Возможность формального вывода в этом исчислении любой тождественно истинной формулы была решена К. Гёделем. Однако в случае бесконечных предметных областей установление содержательной полноты исчисления предикатов требует привлечения средств, выходящих за пределы конечной (финитной) математики.
В противоположность содержательной полноте, называемой также полнотой в широком смысле, полнота в узком смысле уже не имеет места в исчислении предикатов.
Действительно, к числу аксиом исчисления предикатов присоединим формулу 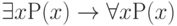 , не выводимую в этом исчислении, но не приводящую к противоречию, если предметная область состоит из единственного объекта. Если предметная область состоит из двух объектов х и у, указанная аксиома превращается в формулу
, не выводимую в этом исчислении, но не приводящую к противоречию, если предметная область состоит из единственного объекта. Если предметная область состоит из двух объектов х и у, указанная аксиома превращается в формулу 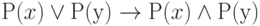 , не являющуюся тождественно истинной и потому не выводимую из остальных аксиом.
, не являющуюся тождественно истинной и потому не выводимую из остальных аксиом.
Наряду с тождественно истинными формулами, в исчислении предикатов рассматривают так называемые выполнимые формулы.
Выполнимой будем называть такую формулу, которая может быть истинной при выборе подходящей предметной области и при должном определении заданных на ней предикатов.
При такой постановке обратной, в каком-то смысле, задачи первична формула, а вторичны условия, при которых она выполняется, становясь тождественно истинной, а не наоборот. Предполагается, что формула имеет общий вид и не содержит символов индивидуальных предметов и индивидуальных предикатов.
Каждая тождественно истинная формула является и выполнимой. Обратное в общем случае неверно. Примером выполнимой, но не тождественно истинной формулы может служить формула, рассмотренная выше, 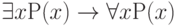 . Эта формула является тождественно истинной лишь на таких предметных областях, которые состоят из одного-единственного объекта.
. Эта формула является тождественно истинной лишь на таких предметных областях, которые состоят из одного-единственного объекта.
Проблема разрешимости для исчисления предикатов состоит в том, чтобы указать единый эффективный алгоритм для определения выполнимости или невыполнимости любой заданной формулы исчисления предикатов на какой-либо предметной области.
В отличие от исчисления высказываний, проблема разрешимости в общем случае для исчисления предикатов, как показали Чёрч и Тьюринг, вообще не имеет решения. Иными словами, не существует единого конструктивного приёма для установления выполнимости или невыполнимости любой формулы исчисления предикатов.
Часто проблема разрешимости для исчисления предикатов формулируется несколько в иной форме: найти алгоритм для определения тождественной истинности любой данной формулы в этом исчислении.
Таким образом, в отношении проблемы разрешимости, исчисление предикатов коренным образом отличается от исчисления высказываний.
Если ограничиться частными видами формул, то разрешающий алгоритм может быть построен и в случае исчисления предикатов.
Такой алгоритм можно, например, построить для формул исчисления предикатов, содержащих лишь одноместные предикаты. Для установления выполнимости или невыполнимости формулы, содержащей n одноместных предикатов, достаточно ограничиться рассмотрением предметных областей, состоящих не более чем из 2n объектов. В результате проверка выполнимости (или тождественной истинности) предикатной формулы (после замены кванторов конъюнкциями или дизъюнкциями) сводится к проверке выполнимости (или, соответственно, тождественной истинности) полученной формулы исчисления высказываний.
В общем случае при решении вопроса о выполнимости или невыполнимости конкретной формулы существенную помощь может оказать предварительное приведение этой формулы к так называемой нормальной форме.
Различают два вида нормальных форм: предварённую форму и нормальную форму Сколема.
Предварённая форма отличается тем, что все кванторы, если они имеются, должны быть вынесены в самое начало формулы, а область действия каждого из них должна распространяться до конца этой формулы.
В нормальной форме Сколема требуется дополнительно, чтобы все кванторы существования предшествовали всем кванторам общности.
Если формула записана в предварённом виде, то её часть, стоящая после кванторов (бескванторная часть формулы), может рассматриваться как формула исчисления высказываний. Каждый предикат рассматривается при этом просто как переменное высказывание. Тогда в этой формуле можно исключить все знаки импликации, заменяя конструкции вида  через
через  , а затем привести её к дизъюнктивной нормальной форме. Такое преобразование приводит исходную предикатную формулу к эквивалентной ей предикатной формуле.
, а затем привести её к дизъюнктивной нормальной форме. Такое преобразование приводит исходную предикатную формулу к эквивалентной ей предикатной формуле.
Справедлива теорема:
Теорема 3.3. Для всякой формулы  (узкого) исчисления предикатов существует эквивалентная ей формула
(узкого) исчисления предикатов существует эквивалентная ей формула  , записанная в предварённой форме. Существует единый алгоритм приведения произвольной предикатной формулы к предварённой форме.
, записанная в предварённой форме. Существует единый алгоритм приведения произвольной предикатной формулы к предварённой форме.
Справедливость сформулированной теоремы вытекает из легко проверяемых соотношений:
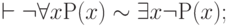 |
( 3.62) |
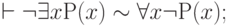 |
( 3.63) |
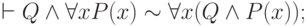 |
( 3.64) |
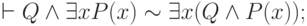 |
( 3.65) |
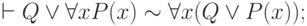 |
( 3.66) |
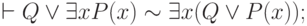 |
( 3.67) |
Поскольку импликация может быть заменена операциями дизъюнкции и отрицания, то с помощью выписанных формул при соблюдении условий, исключающих возможность возникновения коллизии переменных, можно производить последовательную перестановку кванторов со всеми составляющими формулу символами, отличными от кванторов, пока все кванторы не окажутся в левой части формулы.
Приведём пример подобного преобразования:
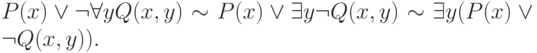
Последняя формула соответствует требуемой предварённой форме исходной формулы.
Для нормальной формы Сколема прямого аналога теоремы 3.3 не существует: не для всякой формулы исчисления предикатов существует эквивалентная формула, имеющая нормальную форму Сколема.
Однако понятие эквивалентности может быть так обобщено, что любую формулу исчисления предикатов можно будет привести к нормальной форме Сколема.
Введём понятие дедуктивной эквивалентности.
Формула  называется дедуктивно эквивалентной формуле
называется дедуктивно эквивалентной формуле  , если, присоединив формулу
, если, присоединив формулу  к системе аксиом исчисления предикатов, получим возможность вывести формулу
к системе аксиом исчисления предикатов, получим возможность вывести формулу  из расширенной системы аксиом и наоборот, присоединив к системе аксиом формулу
из расширенной системы аксиом и наоборот, присоединив к системе аксиом формулу  , получим возможность вывести формулу
, получим возможность вывести формулу  .
.
Это определение применимо не только к исчислению предикатов, но и к любому логическому исчислению, в том числе к исчислению высказываний.
Легко видеть по рассмотренному выше примеру, что обычная эквивалентность формул влечёт их дедуктивную эквивалентность.
Справедлива следующая теорема Сколема:
Теорема 3.4. Для всякой формулы узкого исчисления предикатов существует дедуктивно эквивалентная ей формула, записанная в нормальной форме Сколема. Существует алгоритм приведения любой формулы к дедуктивно эквивалентной ей сколемской форме.
Очевидно, что если две формулы дедуктивно эквивалентны, то из тождественной истинности одной следует тождественная истинность другой. То есть, приведя формулу к нормальной форме Сколема, следует решать проблему тождественной истинности относительно этой формы.
Это же обстоятельство может быть использовано при доказательстве содержательной полноты исчисления предикатов, поскольку для такого доказательства достаточно установить выводимость всех тождественно истинных формул, записанных в нормальной форме Сколема. Действительно, установив выводимость всех указанных формул, мы тем самым установим и выводимость всех дедуктивно эквивалентных им формул, т.е. всех тождественно истинных формул исчисления предикатов.
Известно большое количество классов формул, для которых проблема разрешимости решается положительно. Ограничения, с помощью которых выделяются указанные классы, касаются не только характера, числа и порядка расположения кванторов, но и вида бескванторных частей формул, записанных в предварённой нормальной форме.
Известны исследования возможности построения разрешающих процедур за пределами узкого исчисления предикатов, в частности, - процедур разрешения некоторых формул исчисления предикатов второй ступени. В этом исчислении используются не только предметные, но и предикатные кванторы ("для любого предиката Р", "существует такой предикат Р"). Однако предикаты могут зависеть только от предметных переменных и не могут быть включены в число предметов, составляющих предметную область.
Краткие итоги
- Булева алгебра является основой построения не только цифровых компьютеров, её принципы легли в основу построения ещё более общих и мощных логических исчислений, позволяющих формализовать логическое мышление человека.
- Исчисление высказываний основано на ограниченной аксиоматике, отделено от смысла объектов высказываний, и потому не даёт полного представления о действительно логическом подходе к определению истинности. Например, высказывание
 является истинным, но не отражающим смысл высказываний.
является истинным, но не отражающим смысл высказываний. - Исчисление предикатов расширяет исчисление высказываний привлечением предметной области. Применение кванторов общности и существования позволяет расширить возможности логических преобразований на основе расширенной аксиоматики.
- Задача определения тождественной истинности высказываний (предикатов) является главной задачей любого логического исчисления.
- В исчислении предикатов в большинстве случаев для решения теоретически неразрешимой проблемы определения тождественной истинности используется нормальные формы - предварённая и Сколема, для которых известны алгоритмы приведения.
- Математическая логика событий построена на основе исчисления предикатов, где предметная область (факторное пространство) является определяющим. Хотя "классическое" исчисление предикатов не распространяется на нечёткие данные.
Вопросы
- Как строится совершенная дизъюнктивная нормальная форма для произвольной логической функции?
- Приведите базовый набор тождественных соотношений.
- Какое логическое исчисление следует считать полным и непротиворечивым?
- Охарактеризуйте содержательный и формальный аспекты проблемы установления тождественной истинности высказываний.
- Охарактеризуйте систему аксиом Клини.
- Как исчисление предикатов развивает исчисление высказываний? Что позволяют кванторы общности и существования?
- В чём суть теоремы дедукции?
- Как в исчислении предикатов в формальном аспекте пытаются решить проблему установления тождественной истинности? Какие нормальные формы известны для преобразования формул в исчислении предикатов?
