Обретение навыков построения систем ассоциативных вычислений, распознавания символов и принятия решений
…письмоводитель градоначальника, вошедши утром с докладом в его кабинет, увидел такое зрелище: градоначальниково тело, облечённое в вицмундир, сидело за письменным столом, а перед ним, на кипе недоимочных реестров, лежала, в виде щегольского пресс-папье, совершенно пустая градоначальникова голова.
М.Е. Салтыков-Щедрин. История одного города.
Введение в ассоциативные вычисления
Пусть некоторая система характеризуется значениями трёх параметров x, y, z, которые принято называть факторами факторного пространства. Оценка эффективности этой системы сводится к определению некоторых финансовых затрат $, сопряжённых со значениями этих параметров. Математические зависимости для данной оценки отсутствуют, задача является трудно формализуемой.
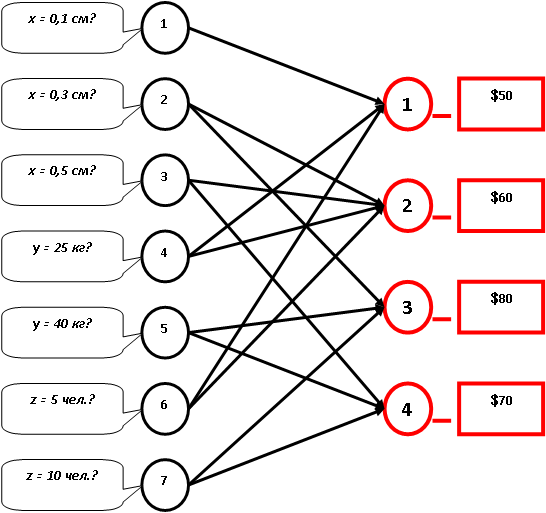
Пусть значение фактора x определяется в сантиметрах (см), значение фактора y – в килограммах (кг), значение фактора z – в количестве человек (чел.), занятых в эксперименте. Составим схему, связав стрелками значения параметров, для которых известны оценки, с этими оценками, как показано на рис. 8.1. Таким образом, схематично представлена некоторая база данных, которую необходимо преобразовать в базу знаний (БЗ), дополнив возможностью логического вывода.
Представим построенную схему, как схему однослойной логической нейронной сети, где слева показан рецепторный слой, а справа – единственный выходной слой нейронов. "Оживим" эту сеть, введя функцию активации нейронов:
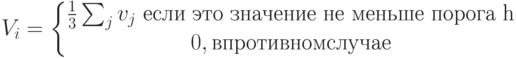 |
( 8.1) |
Здесь Vi (i = 1, 2, 3, 4) – величина возбуждения нейрона выходного слоя, 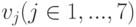 – величина возбуждения рецептора. Выберем h = 0,5.
– величина возбуждения рецептора. Выберем h = 0,5.
Таким образом, на основе опытных данных, в виде обученной логической нейронной сети с единичными весами связей сформирована база знаний, отображающая некоторые финансовые расходы. С помощью данной сети можно производить ассоциативные вычисления для точек факторного пространства, первоначально не представленных на рецепторном слое. Ведь перед пользователем или исследователем возникает вопрос: можно ли для произвольной ситуации в области задания параметров хотя бы приблизительно предсказать связанные с ней расходы?
Рассмотрим пример ассоциативных вычислений для значений x = 0,2 см, y = 30 кг, z = 6 чел. Значение х лежит как раз посредине, между представленными на рецепторном слое значениями х = 1 и х = 3. Тогда полагаем v1 = v2 = 0,5, v3 = 0. Заданное значение y находится между 25 и 40, но ближе к первому. Распределим единицу обратно пропорционально "расстоянию" y = 30 до указанных двух значений и положим v4 = 0,66, v5 = 0,33. Аналогично примем v6 = 0,8, v7 = 0,2. Находим V1 = 0,65, V2 = 0,65, V3 = 0, V4 = 0 и среднее ожидаемое значение затрат
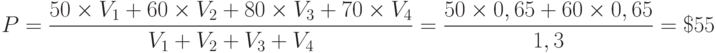
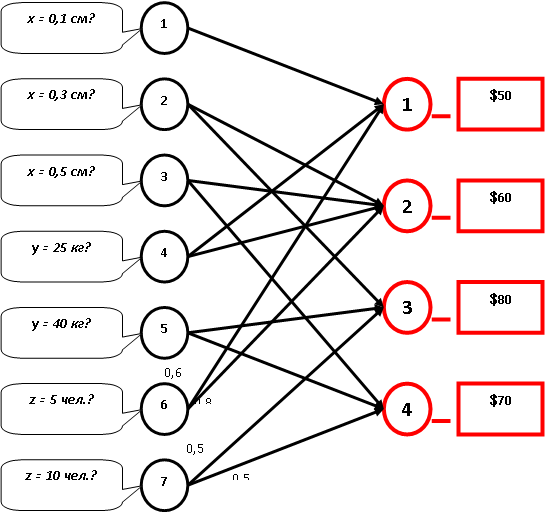
Теперь усложним пример, введя, на основе накопленного опыта и экспериментов, веса связей, как показано на рис. 8.2. (Непомеченные связи – единичные.)
С учётом весов связей целесообразно выбрать другую функцию активации i-го нейрона:
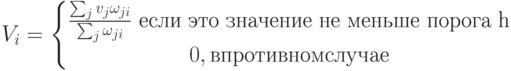 |
( 8.2) |
Здесь Vi – величина возбуждения i-го нейрона, vj – величина возбуждения рецептора, связанного с i-м, 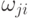 – вес связи j-го рецептора с i-м нейроном.
– вес связи j-го рецептора с i-м нейроном.
Рассчитаем среднее количество затрат для той же ситуации. Возбуждение рецепторов остаётся тем же, и при том же значении h находим V1 = 0,63, V2 = 0,5, V3 = 0, V4 = 0,

Учитывая, что решение могло быть не численным, или допускало бы нечисловую компоненту, сформируем простейшую методику проведения ассоциативных вычислений по логической нейронной сети:
1) Задание исследуемой ситуации на рецепторном слое.
2) Расчёт величины возбуждения нейронов с помощью пороговой функции активации.
3,а) Если все нейроны своим возбуждением указывают на численное значение некоторой величины, находится среднее значение (по возбуждению всех нейронов) в качестве ответа решаемой задачи.
3,б) Если нейроны указывают не на численные значения, например, на текст, символ объекта, качественное значение и пр., находится нейрон с максимальным значением возбуждения (не единственность такового разрешается пользователем, например, уточнением ситуации или рассмотрением дополнительных факторов). Принимается ответ, на который указывает максимально возбудившийся нейрон. Этот процесс выбора подобен голосованию в пользу предпочтительного решения по данной ситуации.
3,в) Если решение представляет собой вектор, то пункты 3,а и 3,б выполняются отдельно для каждой компоненты этого решения. Это означает, что где можно выполнить усреднение, оно производится, где нельзя, на решение указывает максимально возбудившийся нейрон.
Однако ощущение неудовлетворённости мучает нас. Хорошо, действительно – всё так просто! Но как такую нейросеть всунуть в компьютер? Средства мультимедиа, что ли использовать?
Нет. Всё гораздо проще! Логическая нейронная сеть представляется и обрабатывается с помощью матрицы связей. Для рассмотренного примера она представлена в табл. 8.1.