Управление качеством при модернизации и развитии сложных систем в условиях финансовых и технологических ограничений
Научное определение голода было возложено на ветеринаров и на сельский педагогический персонал. ...решено было начать гидротехнические работы. Создана была особая комиссия по набору техников. Но она ни одного техника не приняла, так как оказалось: чтобы построить деревенский колодезь, техник должен знать всего Карла Маркса.
А. Платонов. Город Градов
Задача управления качеством сложной системы
Под сложной системой будем понимать комплекс, как правило, функционально различимых средств, объединённых для совместного решения общей задачи в соответствии с оптимизируемой целевой функцией [26, 27]. Как на теоретическом, так и практическом уровне выделяется класс сложных систем, образующих многоканальные системы массового обслуживания: оборонные, энергетические, транспортные, связи, социальные и пр. В общем случае сложные системы обладают централизованным органом управления и образуют централизованную сеть, узлы которой отображают её объекты. Это представление является условным, так как отдельным объектом, например, справедливо считать комплекс средств связи. Таким образом, понятие "объект" может быть более широким, включающим подсистему средств и даже – рекурсивно – подсистему объектов.
Целевая функция отображает конкретное назначение сложной системы с требуемыми значениями основных параметров обслуживания в соответствии с техническим заданием (ТЗ) на её разработку. Относительно значений этих параметров может быть задано условие их максимизации или минимизации. Это и имеется в виду, когда говорят о оптимизации целевой функции. Например, требуется создать комбинированную сложную систему связи с минимальным временем и с максимальной вероятностью выполнения заявки, соответственно не выше и не ниже заданных значений.
Целевая функция отражает текущие технологические и финансовые возможности. Достижение заданных критериев, обусловленных целевой функцией, говорит о максимальном качестве обслуживания сегодня. Тогда очевидно, что перспективное планирование развития сложных систем требует своевременного обоснования финансируемых направлений исследования и разработок.
На начальном этапе эксплуатации системы могут приниматься решения на более кардинальном уровне: об уточнении ТЗ, о доработке средств и методик испытаний и пр.
Для оптимизации целевой функции целесообразно ввести строго не определяемое понятие текущего качества объекта, как во многом интуитивную, не измеряемую степень его участия в достижении требуемого максимального качества функционирования (обслуживания) сложной системы в целом. Такие оценки определяют текущий рейтинг объекта, который находится экспертным путём.
В общем случае, сложная система обладает конечным жизненным циклом, в течение которого, в результате её деградации, предоставляемое ею качество обслуживания падает до недопустимого уровня. Продление жизни по результатам мониторинга или в соответствии с планом регламентных работ, производится за счёт ремонта и замены отдельных объектов. Однако продления жизни недостаточно, и задача ставится шире: о модернизации и развитии системы в соответствии с современными требованиями, уточняющими целевую функцию, а также с учётом финансовых, технических и технологических возможностей. Модернизация системы противостоит двум основным процессам деградации: "физическому" старению и старению моральному. Однако в процессе эксплуатации сложной системы могут вскрываться конструктивные недоработки объектов и их средств управления, а также ошибки программного обеспечения.
Таким образом, необходимо управлять поддержанием и развитием качества (обслуживания) сложной системы.
Идея такого управления заключается в следующем.
- Организуется периодический контроль объектов сложной системы.
- Для каждого объекта определяется его текущий рейтинг в системе на основе оценки качества выполнения его функций в соответствии с техническими требованиями (ТТ) к системе.
- Если этот рейтинг опустился ниже допустимого уровня, данный объект нуждается в принятии решения о ремонте, замене, смене технологии его изготовления, о изменении алгоритма функционирования системы и др.
- Однако в условиях ограниченного финансирования и доступности технологий, решение принимается по некоторой стратегии комплексно, по множеству объектов недопустимо низкого рейтинга с учётом шкалы важности. При этом, чтобы удовлетворить потребности большего числа "важных" объектов, замена может выполняться по принципу "из того что есть и подешевле".
Рейтинг объектов сложной системы
В основе определения рейтинга отдельного объекта сложной системы лежит ряд показателей, образующих вектор характеристик качества. Как правило, значение этих характеристик или их ограничения обусловлены техническими требованиями (ТТ) или техническим заданием (ТЗ) на разработку системы. К такому уточняемому и расширяемому ряду показателей качества могут относиться:
- пропускная способность или реальная производительность объекта;
- реальная производительность встроенных вычислительных средств объекта;
- среднее время обслуживания запроса;
- вероятность обслуживания;
- частота неудачного решения своей частной задачи;
- частота или количество ложных срабатываний объекта;
- частота отказов объекта с переходом (с требованием перехода) на резерв;
- теоретический расчёт текущей надёжности объекта, например, при Пуассоновском потоке отказов;
- приближение теоретически рассчитанного или объявленного разработчиком срока жизненного цикла объекта;
- применение в основе разработки объекта зарубежной технологии, ставшей "запрещённой";
- снижение отказоустойчивости;
- снижение уровня помехозащищённости;
- нарушение безопасности вычислений встроенных вычислительных средств;
- неудовлетворительные результаты функционального контроля и др.
Для снижения трудоёмкости исследования возможно укрупнение объектов - их объединение в сложные объекты или разбиение всей системы на подсистемы, интерпретируемые как отдельные объекты. Это требует введения некоторой "рейтинговой" алгебры объединения объектов:
- Два объекта участвуют в работе сложной системы по схеме "И", если их совместная функция не может быть выполнена ими порознь. Тогда
Рейтинг((объект1) И (объект2)) = min {рейтинг(объект1), рейтинг(объект2)}. - Два объекта участвуют в работе сложной системы по схеме "ИЛИ", если их совместная функция может быть выполнена хотя бы одним из них. Тогда
Рейтинг((объект1) ИЛИ (объект2)) = max {рейтинг(объект1), рейтинг(объект2)}.
Укрупнение объектов тем более актуально, что характер их взаимодействия часто не позволяет чисто механически производить замену одного объекта более совершенным. Отсутствие сопряжения некоторых характеристик (например, более высокая пропускная способность "нового" объекта) приводит к дисбалансу и к необходимости перенастройки всей подсистемы.
Рейтинговая система на основе интервалов значений показателей качества объектов сложной системы
Построение рейтинговых систем, как класса систем принятия решений, на основе аппарата логических нейронных сетей показано в Лекции 11. Отметим, что все системы принятия решений строятся на однослойных нейронных сетях. Их обработка сводится к простейшей обработке легко модифицируемых матриц следования.
Рассмотрим пример построения типовой рейтинговой системы.
Пусть для данного типа объектов задан вектор характеристик качества {D1, D2, D3, D4}. Диапазон изменения каждой характеристики (типа real) на основе экспертных рекомендаций разбит на три интервала (строго математически, интервалы – полузакрытые или закрытые), принадлежность которым говорит о неизменном рейтинге по данной характеристике на данном интервале её значений:
![D_i \to [d_{i0} – d_{i1}), [d_{i1} – d_{i2}), [d_{i2} – d_{i3}], i = 1, ...,4.](/sites/default/files/tex_cache/706643dcdacb78e34aa7babea92b64b7.png)
В частности, исходя из смысла, di3 может быть равно 0 или  .
.
Интервал [di0 – di1) соответствует диапазону значений характеристики Di (например, производительности), обусловленной ТЗ. Интервал [di1 – di2) соответствует временно допустимому значению этой характеристики. Интервал [di2 – di3] соответствует области значений характеристики Di, где измерения не проведены, либо их значения ниже допустимых (например, производительность снизилась до нуля).
Пусть для построенных интервалов, рассматриваемых совместно, как возможные ситуации на основе вектора характеристик, эксперты установили значения рейтинга из некоторого множества значений: рейтинг высокий, рейтинг средний, рейтинг низкий. То есть, каждой возможной ситуации, описываемой множеством четырёх интервалов, каждый из которых соответствует своей характеристике, задано одно из трёх значений рейтинга.
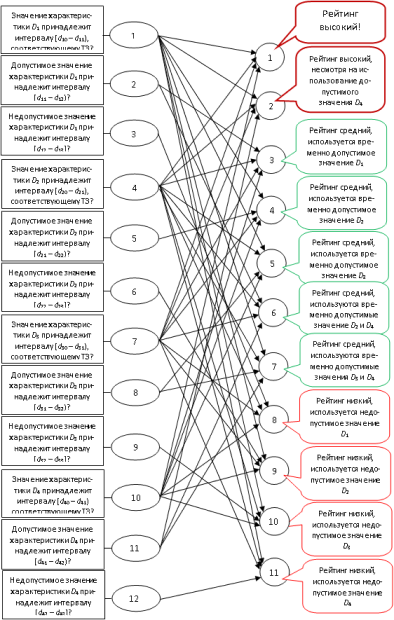
Отобразим на схеме (рис.12.1) пример такого соответствия. При этом все возможные связи воспроизводить не следует, так как низкий рейтинг проявится даже во многих не указанных случаях.
От статического описания базы знаний (БЗ), содержащей связи "ситуация  рейтинг" перейдём к динамической модели ассоциативного мышления, сформировав логическую нейронную сеть. Для этого предположим, что левый столбец пронумерованных овалов соответствует рецепторам, возбуждаемым извне, а правый – нейронам, возбуждение которых от связанных с ними рецепторов указывает на значение рейтинга.
рейтинг" перейдём к динамической модели ассоциативного мышления, сформировав логическую нейронную сеть. Для этого предположим, что левый столбец пронумерованных овалов соответствует рецепторам, возбуждаемым извне, а правый – нейронам, возбуждение которых от связанных с ними рецепторов указывает на значение рейтинга.
Напомним, что возбуждение рецепторов интерпретируется как достоверность высказываний о принадлежности данных, а нейрон представляет собой прибор, выполняющий пороговую функцию активации.
Ситуация же представляет собой набор в данном случае четырёх значений характеристик объекта, принадлежащих соответствующим интервалам.
Для "оживления" модели введём пороговую функцию активации нейрона. Для данного примера такая функция имеет вид:
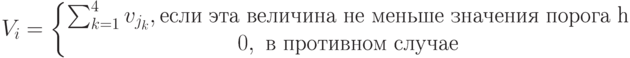
Здесь Vi - величина возбуждения i-го нейрона, vjk, 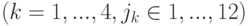 – величина возбуждения одного из четырёх рецепторов, связанных с i-м нейроном. Порог h выбирается экспериментально в процессе эксплуатации рейтинговой системы так, чтобы исключить лишние вычисления.
– величина возбуждения одного из четырёх рецепторов, связанных с i-м нейроном. Порог h выбирается экспериментально в процессе эксплуатации рейтинговой системы так, чтобы исключить лишние вычисления.
Для иллюстрации выберем некоторый объект, то есть, некоторую ситуацию, заданную конкретными значениями характеристик качества. Не вдаваясь в "физический смысл", предположим, что значение d1 характеристики D1 принадлежит интервалу [d10 – d11). Задаём возбуждение рецептора: v1 = 1. Пусть точно не определена принадлежность значения d2 характеристики D2, однако есть предположение, что с вероятностью 0,6 это значение принадлежит интервалу [d20 – d21), а с вероятностью 0,4 - интервалу [d21 – d22). Возбуждаем рецепторы: v4 = 0,6, v5 = 0,4. Пусть известно, что значение d3 характеристики D3 принадлежит интервалу [d30 – d31), а значение d4 характеристики D4 принадлежит интервалу [d40 – d41). Полагаем v7 = v10 = 1. Пусть из соображений трудоёмкости дальнейшего анализа, экспериментально, выбран порог h = 0,7. Рассчитаем значение функции активации всех нейронов: V1 = 0,9, V2 = V3 = 0, V4 = 0,85, V5 = V6 = V7 = V8 = V9 = V10 = V11 = 0. Максимально возбудившийся нейрон 1 формально указывает на высокий рейтинг объекта. Однако тревожность ситуации нельзя не заметить по высокому возбуждению нейрона 4, указывающего на средний рейтинг.
В рассмотренной рейтинговой системе вместо интервалов могут указываться данные типа integer или Boolean – в любой комбинации, могут быть указаны объекты, входящие в состав данного и т.д. Так, например, может учитываться наличие или отсутствие аппаратного контроля вычислительных средств, применение кодов, корректирующих ошибки, наличие и состояние специальных подъездных путей и др.
Развитие рейтинговой системы связано с введением весов связей, как степени влияния разных характеристик качества или даже их значений на общий показатель рейтинга объекта. Как правило, эти веса определяются в результате длительной эксплуатации системы. Не желая загромождать рис. 12.1, легко представить на стрелках, наличие которых на рисунке указывает на единичные веса, отличные от нуля веса 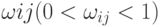 связей, ведущих от j-го рецептора к i-му нейрону. С учётом весов связей функция активации i-го нейрона имеет вид:
связей, ведущих от j-го рецептора к i-му нейрону. С учётом весов связей функция активации i-го нейрона имеет вид:
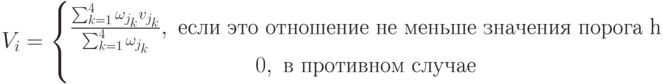
При обработке логической нейронной сети используется матрица связей. Для данного примера, но для случая, когда некоторые веса меньше единицы (пусть это выяснилось в процессе длительной эксплуатации), такая матрица имеет вид табл.12.1.
| Рецепторы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Решение нейрона 1 | 1 | 1 | 1 | 1 | ||||||||
| Решение нейрона 2 | 1 | 1 | 1 | 1 | ||||||||
| Решение нейрона 3 | 1 | 1 | 1 | 1 | ||||||||
| Решение нейрона 4 | 1 | 1 | 1 | 0,8 | ||||||||
| Решение нейрона 5 | 1 | 1 | 1 | 1 | ||||||||
| Решение нейрона 6 | 1 | 1 | 1 | 1 | ||||||||
| Решение нейрона 7 | 1 | 1 | 1 | 1 | ||||||||
| Решение нейрона 8 | 1 | 1 | 1 | 0,9 | ||||||||
| Решение нейрона 9 | 1 | 1 | 1 | 1 | ||||||||
| Решение нейрона 10 | 1 | 1 | 1 | 1 | ||||||||
| Решение нейрона 11 | 1 | 1 | 1 | 1 |
Отображение системой концентрических областей одинакового рейтинга
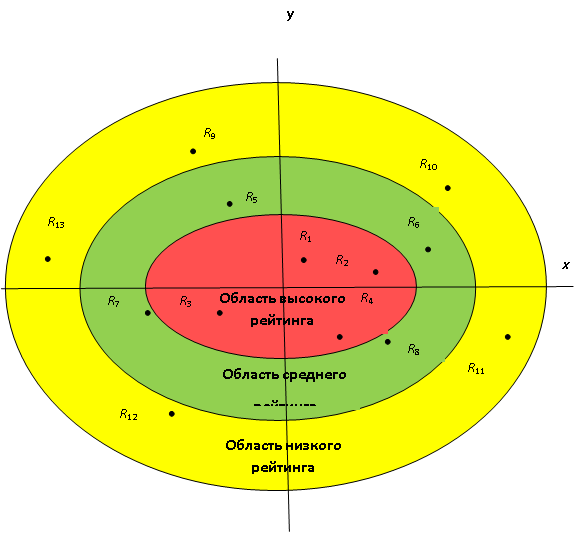
Наглядное отображение рейтинга объекта на экране основано на попадании точки, соответствующей характеристикам объекта, в некоторую рейтинговую область (рис. 12.2). Однако в этом случае затруднены текстовые комментарии к выводам, объясняющие принимаемые решения о рейтинге, как это показано на рис. 12.1.
Для построения системы концентрических рейтинговых областей используется плоская, "сплющенная" по размеру экрана сферическая система координат, рассмотренная в Лекции 11. Каждая точка характеризуется значением радиуса r и угла  .
.
В рейтинговых областях сначала произвольно размещаются точки, которым затем ставятся в соответствие условные объекты-эталоны с численными значениями показателей качества. Так формируются связи "вектор значений показателей качества – сферические координаты точки на экране". В результате нейросетевой обработки испытываемого объекта с его показателями качества в соответствующей ему рейтинговой области формируется точка.
В Лекции 11 рассмотрен пример возможного банковского мониторинга с помощью концентрических рейтинговых областей. В качестве эталонных банков различного рейтинга там могли использоваться как существующие, так и предполагаемые банки в соответствии с оценкой экспертов. Так как в рассматриваемой постановке задачи не допускается существование действующей сложной системы с низким рейтингом, то за эталоны должны приниматься условные объекты, для которых численные характеристики качества входят в интервалы, указанные в разделе 12.3, образуя варианты этих объектов различного рейтинга. Таким образом, множество эталонных объектов различного рейтинга, соответствующих точкам R1, ..., R13 на экране, строится с помощью логической нейронной сети на рис. 12.1.
Продолжая рассмотрение примера, предположим, что значения характеристик 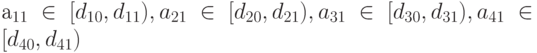 определяют эталонный вариант 1 исследуемого объекта, которому на экране соответствует точка
определяют эталонный вариант 1 исследуемого объекта, которому на экране соответствует точка 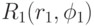 в области высокого рейтинга.
в области высокого рейтинга.
Предположим, что тем же интервалам принадлежат значения характеристик a12, a22, a32, a42, определяющие эталонный вариант 2 исследуемого объекта, которому на экране соответствует точка  в области высокого рейтинга. То же предположим относительно значений характеристик a13, a23, a33, a43, определяющих эталонный вариант 3 исследуемого объекта, которому на экране соответствует точка
в области высокого рейтинга. То же предположим относительно значений характеристик a13, a23, a33, a43, определяющих эталонный вариант 3 исследуемого объекта, которому на экране соответствует точка  в области высокого рейтинга. Для получения точки
в области высокого рейтинга. Для получения точки 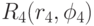 предположим, что значение a44 характеристики D4 принадлежит интервалу [d41, d42).
предположим, что значение a44 характеристики D4 принадлежит интервалу [d41, d42).
Аналогично выбираются значения характеристик качества объекта, принадлежащие диапазонам их изменения, определяющим средний рейтинг.
Пусть значения a15, a25, a35, a45 соответствуют точке 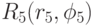 ;
;
....................................................
значения a18, a28, a38, a48 соответствуют точке 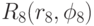 .
.
Таким же образом точками объектов-эталонов 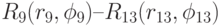 наполняется область низкого рейтинга. Точке R9 соответствует набор значений a19, a29, a39, a49, ..., точке R13 соответствует набор а1,13, a2,13, a3,13, a4,13.
наполняется область низкого рейтинга. Точке R9 соответствует набор значений a19, a29, a39, a49, ..., точке R13 соответствует набор а1,13, a2,13, a3,13, a4,13.
Построенное соответствие векторов характеристик качества объекта точкам различного рейтинга на экране определило содержимое базы знаний (БЗ).
Для формирования логической нейронной сети упорядочим в порядке возрастания все значения a11, a12, ..., a1,13 характеристики D1, фигурирующие в выше приведённых построениях. Предположим, что при выборе значений характеристик качества для эталонных точек не допускалось повторение одних и тех же значений. Обозначим в новом порядке полученную возрастающую последовательность b11, ..., b1,13. Выполним такую же операцию над всеми фигурирующими значениями характеристик D2, D3, D4. Получим возрастающие последовательности b21, ..., b2,13; b31, ..., b3,13; b41, ..., b4,13. Поскольку выбор точек R1, ..., R13 произведён произвольно, по рисунку найдём их приблизительные координаты: R1(2, 60o), R2(8, 15o), R3(7, 210o), R4(4, 310o), R5(9, 120o), R6(13, 20o), R7(14, 200o), R8(12, 320o), R9(16, 120o), R10(16, 30o), R11(16, 330o), R12(15, 230o), R13(17, 170o).
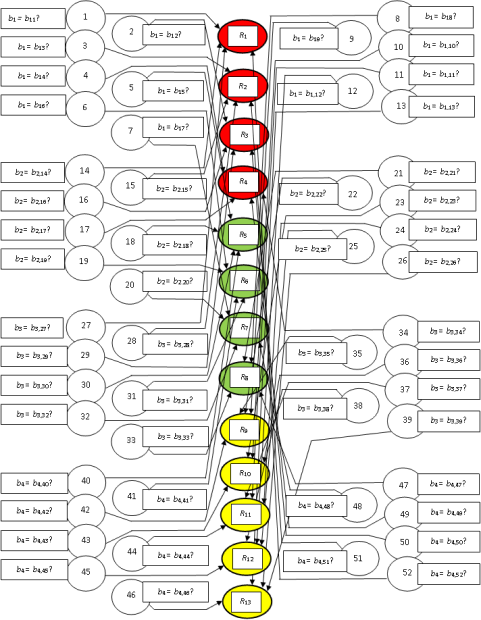
За каждым членом совокупной последовательности значений характеристик качества закрепим рецептор (рис. 12.3). Для данного примера требуется 52 рецептора. Введём 13 нейронов, каждый из которых своим возбуждением указывает на соответствующую точку экрана. Соединим рецепторы, определяющие отдельные точки, с нейронами, соответствующими этим точкам. Тем самым зададим единичные веса связей в полученной логической нейронной сети.
Так как пример не отражает реальные показатели качества, на рисунке показан лишь возможный вариант связей.
Воспользуемся ранее использованной функцией активации для единичных весов связей. Однако положим h = 0, так как для большей точности попадания в "свою" рейтинговую область, желательно сравнивать ситуацию (b1, b2, b3, b4), рейтинг которой следует определить, с большим числом точек базы знаний.
Алгоритм оценки рейтинга объекта сложной системы
- Находятся значения показателей качества объекта, представляющие вектор с численными значениями компонентов.
- Производится возбуждение рецепторов логической нейронной сети. А именно, для данного испытываемого значения bi, где i – индекс показателя качества, находится рецептор, закреплённый за этим значением показателя. Если такой рецептор существует, значение его возбуждения принимается равным единице. Возбуждение других рецепторов данного показателя качества равно нулю. Если такого рецептора нет, находятся два рецептора, закреплённых за меньшим
 и большим
и большим 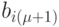 значениями относительно bi. "Единица" распределяется обратно пропорционально "расстоянию" bi до данных рецепторов, образуя их значения возбуждения: возбуждение
значениями относительно bi. "Единица" распределяется обратно пропорционально "расстоянию" bi до данных рецепторов, образуя их значения возбуждения: возбуждение 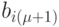 принимается равным
принимается равным 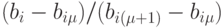 , а возбуждение
, а возбуждение  дополняет это отношение до единицы. Возбуждение других рецепторов данного показателя качества остаётся нулевым. Так находится возбуждение рецепторов для всех показателей качества (для всех i).
дополняет это отношение до единицы. Возбуждение других рецепторов данного показателя качества остаётся нулевым. Так находится возбуждение рецепторов для всех показателей качества (для всех i). - С помощью функции активации находится возбуждение всех нейронов, каждый из которых указывает на эталонную точку экрана.
- Для "возбудившихся" нейронов находится среднее значение радиуса r и угла
 . В качестве весов в формуле нахождения среднего (математического ожидания) используются значения возбуждения нейронов. (Благодаря выбору сферической системы координат, средняя точка не выйдет за пределы рейтинговых областей, которым принадлежат усредняемые точки.)
. В качестве весов в формуле нахождения среднего (математического ожидания) используются значения возбуждения нейронов. (Благодаря выбору сферической системы координат, средняя точка не выйдет за пределы рейтинговых областей, которым принадлежат усредняемые точки.) - Точка
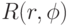 воспроизводится на экране, попав в некоторую область рейтинга объекта.
воспроизводится на экране, попав в некоторую область рейтинга объекта.
О стратегии повышения качества сложных систем в условиях финансовых и технологических ограничений
Тревожное состояние объекта, обусловленное снижением его рейтинга, служит лишь сигналом о необходимости принятия мер по ремонту, замене, модернизации и пр. Меры принимаются комплексно по состоянию всех объектов. Для этого существует или подразумевается шкала важности объектов, определяющая приоритеты при восстановлении или развитии средств сложной системы. Например, предаварийное состояние силового агрегата электростанции требует его ремонта или замены в первую очередь. Однако предаварийное состояние плотины гидроэлектростанции вызывает неотложность мер, ибо прорыв плотины ведёт не к аварии, а к катастрофе.
Важную роль здесь играет человеческий фактор, неотделимый от политических, экономических и военных задач. Не следует забывать о приоритетах научных исследований.
Можно сформулировать математическую задачу оптимизации очерёдности принятия мер по повышению качества на основе важности объектов в условиях финансовых ограничений. Объекты следует выстроить в очередь по важности и по рейтингу и последовательно вычерпывать выделенные финансы затратами на повышение качества объектов. Однако при этом должна учитываться важность самой сложной системы, и математические выкладки вряд ли произведут впечатление на лицо, принимающее решение (ЛПР). Ведь следует учитывать ущерб, наносимый задержкой или полным отсутствием реакции на сигнал о снижении рейтинга объекта.
Таким образом, поиск оптимальной стратегии повышения качества сложной системы после установления рейтинга её объектов превращается в конкретную, но трудно формализуемую задачу высокой сложности. Это задача о разработке системы принятия решений на основе анализа многих информационно трудно совместимых факторов, характеризующихся нечёткими данными. Представляется, что аппарат логических нейронных сетей направлен именно на разработку таких систем принятия решений.
Краткие итоги
- Управление качеством сложной системы направлено на своевременное принятие мер по сохранению и развитию высоких показателей многоканального обслуживания и, прежде всего, – по удовлетворению высокой пропускной способности и производительности, а также высокой надёжности и безопасности.
- Большое количество факторов, лежащих в основе функционирования сложных систем, их целевое, технологическое и типовое разнообразие, не полная возможность численных оценок превращают задачу управления качеством в трудно формализуемую задачу высокой сложности. При решении подобных задач целесообразно применять такие методы и средства искусственного интеллекта, как логические нейронные сети, с использованием экспертных оценок там, где объективные численные измерения невозможны.
- Для каждого типа средств, входящих в состав сложной системы, составляется своя рейтинговая система на основе логической нейронной сети. При этом используются характеристики, свойственные данному типу средств: вычислительных, оборонных, энергетических, строительных и транспортных сооружений и т.д.
- В процессе эксплуатации логической нейронной сети в составе рейтинговой системы эта система (её база знаний) легко развивается, уточняются веса связей, а решения модифицируются для большей результативности.
- По установленным экспертами условным весам средств системы и на основе текущих рейтингов отдельных объектов, по формуле нахождения среднего может быть получен рейтинг сложной системы. Однако он свидетельствует лишь о качестве работы этой системы, и не может служить абсолютной мерой качества при сравнении с другими, даже аналогичными системами, в том числе, с системой "идеальной". Ведь все системы обладают своей целевой функцией!
Вопросы
- В чём заключается идея управления качеством сложной системы?
- Как составляется рейтинговая система управления качеством объекта сложной системы по интервалам значений его характеристик качества?
- В чём идея и как составляется наглядная рейтинговая система управления качеством объекта сложной системы?