|
В уравнениях движения кривошипно-шатунного механизма вместо обозначения радиуса кривошипа "r" ошибочно записан символ "?" (гамма). P.S. Может быть это слишком очевидно, но не упомянуто, что угол поворота кривошипа ? считается малым. |
Случайные события, случайные величины. Их законы распределения и числовые характеристики
Среднее квадратичное отклонение:

Рассмотрим пример, если задана непрерывная случайная величина.
Пусть непрерывная случайная величина задана интегральной функцией распределения:
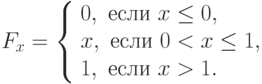
Найдем дифференциальную функцию распределения:
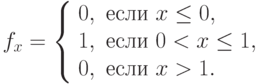
Математическое ожидание X и X2:
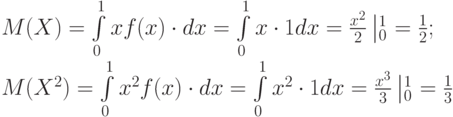
Тогда:
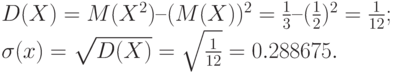
Если равномерно распределенная случайная величина задана в интервале [a,b], то ее математическое ожидание, дисперсия и среднее квадратичное отклонение равны:
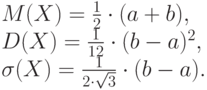
Свойства дисперсии:
- D(C)=0
- D(CX)=C2D(X)
- D(X+Y)=D(X)+D(Y),
- D(C+X)=D(X),
- D(X-Y)=D(X)+D(Y).
Свойство среднеквадратичного отклонения:

Закон нормального распределения вероятностей непрерывной случайной величины занимает особое место среди различных теоретических законов, т. к. является основным во многих практических исследованиях, им описывается большинство случайных явлений, связанных с производственными процессами.
К случайным явлениям, подчиняющимся нормальному закону распределения, относятся ошибки измерений производственных параметров, распределение технологических погрешностей изготовления, рост и вес большинства биологических объектов, распределение параметров пленочных резисторов и др.
Нормальным называют закон распределения вероятностей непрерывной случайной величины, который описывается дифференциальной функцией
 |
( 6.5) |
где
a - математическое ожидание случайной величины;
 -среднее квадратичное отклонение нормального распределения.
-среднее квадратичное отклонение нормального распределения.
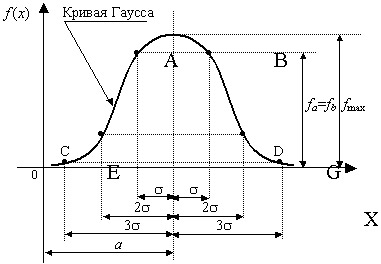
График дифференциальной функции нормального распределения называют нормальной кривой (кривой Гаусса) (рис. 6.7).
Свойства нормальной кривой (кривой Гаусса):
- Кривая симметрична относительно прямой x = a.
- Нормальная кривая расположена над осью X, т. е. при всех значениях X функция f(x) всегда положительна.
- Ось X является горизонтальной асимптотой графика, т. к.
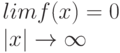
- При x = a функция f(x) имеет максимум равный
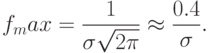
- В точках A и B при
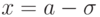 и
и  кривая имеет точки перегиба, ординаты которых равны.
кривая имеет точки перегиба, ординаты которых равны.
При этом, вероятность того, что абсолютная величина отклонения случайной величины, распределенной нормально, от ее математического ожидания не превысит среднего квадратичного отклонения
 , равна 0,6826.
, равна 0,6826. - В точках E и G, при
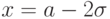 и
и 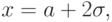 значение функции f(x) равноа вероятность того, что абсолютная величина отклонения случайной величины, распределенной нормально, от ее математического ожидания не превысит удвоенного среднего квадратичного отклонения, равна 0,9544.
значение функции f(x) равноа вероятность того, что абсолютная величина отклонения случайной величины, распределенной нормально, от ее математического ожидания не превысит удвоенного среднего квадратичного отклонения, равна 0,9544.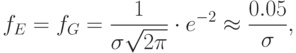
- Асимптотически приближаясь к оси абсцисс, кривая Гаусса в точках C и D, при
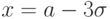 и
и 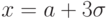 , очень близко подходит к оси абсцисс. В этих точках значение функции f(x) очень малоа вероятность того, что абсолютная величина отклонения случайной величины, распределенной нормально, от ее математического ожидания не превысит утроенного среднего квадратичного отклонения, равна 0,9973. Это свойство кривой Гаусса называется "правило трех сигм".
, очень близко подходит к оси абсцисс. В этих точках значение функции f(x) очень малоа вероятность того, что абсолютная величина отклонения случайной величины, распределенной нормально, от ее математического ожидания не превысит утроенного среднего квадратичного отклонения, равна 0,9973. Это свойство кривой Гаусса называется "правило трех сигм".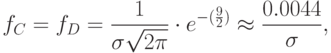
Изменение величины параметра a (математического ожидания случайной величины) не изменяет форму нормальной кривой, а приводит лишь к ее смещению вдоль оси X: вправо, если a возрастает, и влево, если a убывает.
При a=0 нормальная кривая симметрична относительно оси ординат.