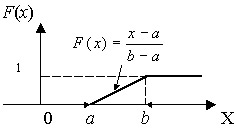НОУ ИНТУИТ | Введение в математическое моделирование. Лекция 6: Случайные события, случайные величины. Их законы распределения и числовые характеристики

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Донецкий национальный технический университет

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 5968 / 2125 | Оценка: 4.11 / 3.78 | Длительность: 12:32:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 68 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Свойства дифференциальной функции распределения:

Дифференциальная функция распределения неотрицательна, т. е. $f(x)\ge 0$
Если все возможные значения случайной величины принадлежат интервалу (a, b), то
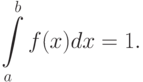
$\int\limits_a^b f(x)dx =1.$

Так как дифференциальная функция распределения равна f(x)=F’(x), то можно записать

$f(x)=lim \frac{F(x+ \Delta x) – F(x)}{\Delta x}, \Delta x \to 0,$

( 6.1)

т. е. предел отношения вероятности того, что непрерывная случайная величина примет значение, принадлежащее интервалу 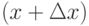$(x+\Delta x)$ к длине этого интервала 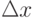$\Delta x$ (при $\Delta x \to 0$ ), равен значению дифференциальной функции распределения в точке x.

Аналогичное (6.1) определение дается в механике для определения плотности массы в точке (если масса распределена вдоль оси X по закону F(x) ), поэтому в теории вероятности для дифференциальной функции распределения f(x) часто используется термин "плотность вероятности в точке".

На основании (6.1) запишем:

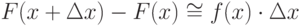$F(x+ \Delta x)-F(x) \cong f(x) \cdot \Delta x$

( 6.2)

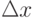Вероятностный смысл дифференциальной функции распределения на основании (6.2) таков: вероятность того, что случайная величина примет значение принадлежащее интервалу $(x, x + \Delta x)$ приближенно равна произведению плотности вероятности в точке x на длину интервала $\Delta x$ или (на графике) площади прямоугольника с основанием 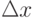$\Delta x$ и высотой f(x).

Дифференциальную функцию распределения часто называют законом распределения вероятностей непрерывных случайных величин.

При решении прикладных задач сталкиваются с различными законами распределения вероятностей непрерывных случайных величин. Часто встречаются законы равномерного и нормального распределения.

Примечание. Отметим, что законом распределения вероятностей дискретных случайных величин, называют соответствие между возможными значениями дискретной случайной величины и вероятностями их появления. Вероятности можно задать таблично, аналитически (биномиальное распределение по формуле Бернулли, распределение Пуассона) или графически (в виде многоугольника распределения).

Закон равномерного распределения вероятностей непрерывной случайной величины используется при имитационном моделировании сложных систем на ЭВМ как первоначальная основа для получения всех необходимых статистических моделей. При этом, если специально не оговорен закон распределения случайных чисел, то имеют ввиду равномерное распределение.

Распределение вероятностей называют равномерным, если на интервале (a,b), которому принадлежат все возможные значения случайной величины, дифференциальная функция распределения имеет постоянное значение, т. е. f(x) = C.

Так как

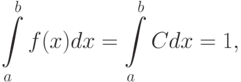
$\int \limits_a^b f(x)dx = \int \limits_a^b Cdx = 1,$

то

$C=\frac{1}{\int \limits_a^b dx} = \frac{1}{b-a}.$

Отсюда закон равномерного распределения аналитически можно записать так:

$f(x)=\left\{ \begin{array}{l} 0, x \le a,\\ \frac{1}{b-a}, a < x \le b,\\ 0, x > b, \end{array} \right.$

График дифференциальной функции равномерного распределения вероятностей представлен на рис. 6.5

Рис. 6.5.

Интегральную функцию равномерного распределения аналитически можно записать так:

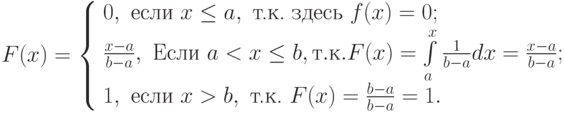
$F(x)=\left\{ \begin{array}{l} 0, \text{ если } x\le a, \text{ т.к. здесь } f(x)=0;\\ \frac{x-a}{b-a}, \text{ Если } a < x\le b, т.к. F(x)=\int\limits_a^x \frac{1}{b-a}dx=\frac{x-a}{b-a};\\ 1, \text{ если } x > b, \text{ т.к. } F(x)=\frac{b-a}{b-a}=1. \end{array} \right.$

График интегральной функции равномерного распределения вероятностей представлен на рис. 6.6

Рис. 6.6.

Закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится пользоваться, так называемыми, числовыми характеристиками случайной величины. К ним относятся:

Математическое ожидание M,
Дисперсия D,
Среднее квадратичное отклонение $\sigma$ .

Математическое ожидание дискретной случайной величины X – это сумма произведений всех ее возможных значений $x_i, i=\overline{1,n}$ на их вероятности $p_i, i=\overline{1,n}$ .

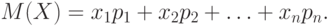$M(X) = x_1p_1 + x_2p_2 + \ldots + x_np_n.$

( 6.3)

Математическое ожидание непрерывной случайной величины X, возможное значение которой принадлежит отрезку [a,b] – это определенный интеграл

$M(X)=\int\limits_a^b xf(x)dx$

( 6.4)

Последнее определение (для непрерывной случайной величины) получено на основании того, что вероятность попадания X в интервал $\Delta x$ приблизительно равна $f(x)\cdot\Delta x$ ..

Математическое ожидание случайной величины (как дискретной, так и непрерывной) есть неслучайная (постоянная) величина. Она характеризует среднее значение случайной величины.

Дальше >>

Авторизоваться

Введение в математическое моделирование

Случайные события, случайные величины. Их законы распределения и числовые характеристики

Вопросы и ответы