Компьютерное имитационное моделирование. Статистическое имитационное моделирование

Компьютерное моделирование как новый метод научных исследований основывается на:

1. построении математических моделей для описания изучаемых процессов;
2. использовании новейших вычислительных машин, обладающих высоким быстродействием (миллионы операций в секунду) и способных вести диалог с человеком.

Суть компьютерного моделирования состоит в следующем: на основе математической модели с помощью ЭВМ проводится серия вычислительных экспериментов, т.е. исследуются свойства объектов или процессов, находятся их оптимальные параметры и режимы работы, уточняется модель. Например, располагая уравнением, описывающим протекание того или иного процесса, можно изменяя его коэффициенты, начальные и граничные условия, исследовать, как при этом будет вести себя объект. Имитационные модели - это проводимые на ЭВМ вычислительные эксперименты с математическими моделями, имитирующими поведение реальных объектов, процессов или систем.

Реальные процессы и системы можно исследовать с помощью двух типов математических моделей: аналитических и имитационных.

В аналитических моделях поведение реальных процессов и систем (РПС) задается в виде явных функциональных зависимостей (уравнений линейных или нелинейных, дифференциальных или интегральных, систем этих уравнений). Однако получить эти зависимости удается только для сравнительно простых РПС. Когда явления сложны и многообразны исследователю приходится идти на упрощенные представления сложных РПС. В результате аналитическая модель становится слишком грубым приближением к действительности. Если все же для сложных РПС удается получить аналитические модели, то зачастую они превращаются в трудно разрешимую проблему. Поэтому исследователь вынужден часто использовать имитационное моделирование.

Имитационное моделирование представляет собой численный метод проведения на ЭВМ вычислительных экспериментов с математическими моделями, имитирующими поведение реальных объектов, процессов и систем во времени в течение заданного периода. При этом функционирование РПС разбивается на элементарные явления, подсистемы и модули. Функционирование этих элементарных явлений, подсистем и модулей описывается набором алгоритмов, которые имитируют элементарные явления с сохранением их логической структуры и последовательности протекания во времени.

Имитационное моделирование - это совокупность методов алгоритмизации функционирования объектов исследований, программной реализации алгоритмических описаний, организации, планирования и выполнения на ЭВМ вычислительных экспериментов с математическими моделями, имитирующими функционирование РПС в течение заданного периода.

Под алгоритмизацией функционирования РПС понимается пооперационное описание работы всех ее функциональных подсистем отдельных модулей с уровнем детализации, соответствующем комплексу требований к модели.

"Имитационное моделирование" (ИМ)- это двойной термин. "Имитация" и "моделирование" - это синонимы. Фактически все области науки и техники являются моделями реальных процессов. Чтобы отличить математические модели друг от друга, исследователи стали давать им дополнительные названия. Термин "имитационное моделирование" означает, что мы имеем дело с такими математическими моделями, с помощью которых нельзя заранее вычислить или предсказать поведение системы, а для предсказания поведения системы необходим вычислительный эксперимент (имитация) на математической модели при заданных исходных данных.

Основное достоинство ИМ:

1. возможность описания поведения компонент (элементов) процессов или систем на высоком уровне детализации;
2. отсутствие ограничений между параметрами ИМ и состоянием внешней среды РПС;
3. возможность исследования динамики взаимодействия компонент во времени и пространстве параметров системы;

Эти достоинства обеспечивают имитационному методу широкое распространение.

Рекомендуется использовать имитационное моделирование в следующих случаях:

1. Если не существует законченной постановки задачи исследования и идет процесс познания объекта моделирования. Имитационная модель служит средством изучения явления.
2. Если аналитические методы имеются, но математические процессы сложны и трудоемки, и имитационное моделирование дает более простой способ решения задачи.
3. Когда кроме оценки влияния параметров (переменных) процесса или системы желательно осуществить наблюдение за поведением компонент (элементов) процесса или системы (ПС) в течение определенного периода.
4. Когда имитационное моделирование оказывается единственным способом исследования сложной системы из-за невозможности наблюдения явлений в реальных условиях (реакции термоядерного синтеза, исследования космического пространства).
5. Когда необходимо контролировать протекание процессов или поведение систем путем замедления или ускорения явлений в ходе имитации.
6. При подготовке специалистов для новой техники, когда на имитационных моделях обеспечивается возможность приобретения навыков в эксплуатации новой техники.
7. Когда изучаются новые ситуации в РПС. В этом случае имитация служит для проверки новых стратегий и правил проведения натурных экспериментов.
8. Когда особое значение имеет последовательность событий в проектируемых ПС и модель используется для предсказания узких мест в функционировании РПС.

Однако ИМ наряду с достоинствами имеет и недостатки:

1. Разработка хорошей ИМ часто обходится дороже создания аналитической модели и требует больших временных затрат.
2. Может оказаться, что ИМ неточна (что бывает часто), и мы не в состоянии измерить степень этой неточности.
3. Зачастую исследователи обращаются к ИМ, не представляя тех трудностей , с которыми они встретятся и совершают при этом ряд ошибок методологического характера.

И тем не менее ИМ является одним из наиболее широко используемых методов при решении задач синтеза и анализа сложных процессов и систем.

Одним из видов имитационного моделирования является статистическое имитационное моделирование, позволяющее воспроизводить на ЭВМ функционирование сложных случайных процессов.

При исследовании сложных систем, подверженных случайным возмущениям используются вероятностные аналитические модели и вероятностные имитационные модели.

В вероятностных аналитических моделях влияние случайных факторов учитывается с помощью задания вероятностных характеристик случайных процессов (законы распределения вероятностей, спектральные плотности или корреляционные функции). При этом построение вероятностных аналитических моделей представляет собой сложную вычислительную задачу. Поэтому вероятностное аналитическое моделирование используют для изучения сравнительно простых систем.

Подмечено, что введение случайных возмущений в имитационные модели не вносит принципиальных усложнений, поэтому исследование сложных случайных процессов проводится в настоящее время, как правило, на имитационных моделях.

В вероятностном имитационном моделировании оперируют не с характеристиками случайных процессов, а с конкретными случайными числовыми значениями параметров ПС. При этом результаты, полученные при воспроизведении на имитационной модели рассматриваемого процесса, являются случайными реализациями. Поэтому для нахождения объективных и устойчивых характеристик процесса требуется его многократное воспроизведение, с последующей статистической обработкой полученных данных. Именно поэтому исследование сложных процессов и систем, подверженных случайным возмущениям, с помощью имитационного моделирования принято называть статистическим моделированием.

Статистическая модель случайного процесса - это алгоритм, с помощью которого имитируют работу сложной системы, подверженной случайным возмущениям; имитируют взаимодействие элементов системы, носящих вероятностный характер.

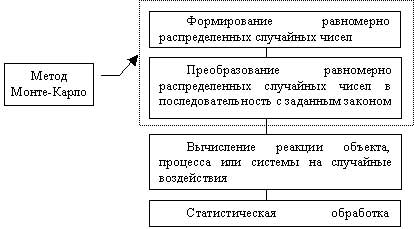
При реализации на ЭВМ статистического имитационного моделирования возникает задача получения на ЭВМ случайных числовых последовательностей с заданными вероятностными характеристиками. Численный метод, решающий задачу генерирования последовательности случайных чисел с заданными законами распределения, получил название "метод статистических испытаний" или "метод Монте-Карло".

Так как метод Монте-Карло кроме статистического моделирования имеет приложение к ряду численных методов (взятие интегралов, решение уравнений), то целесообразно иметь различные термины.

Итак, статистическое моделирование - это способ изучения сложных процессов и систем, подверженных случайным возмущениям, с помощью имитационных моделей.

Метод Монте-Карло - это численный метод, моделирующий на ЭВМ псевдослучайные числовые последовательности с заданными вероятностными характеристиками.

Методика статистического моделирования состоит из следующих этапов:

1. Моделирование на ЭВМ псевдослучайных последовательностей с заданной корреляцией и законом распределения вероятностей (метод Монте-Карло), имитирующих на ЭВМ случайные значения параметров при каждом испытании;
2. Преобразование полученных числовых последовательностей на имитационных математических моделях.
3. Статистическая обработка результатов моделирования.

Обобщенный алгоритм метода статистических испытаний представлен на рис. 5.1.

Рис. 5.1. Обобщенный алгоритм метода статистических испытаний