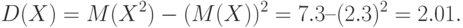Случайные события, случайные величины. Их законы распределения и числовые характеристики

Свойства математического ожидания:

1. M(C)=C – математическое ожидание константы равно самой константе
2. 
3. 
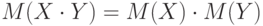
4. M(X+Y)=M(X)+M(Y)

Вероятностный смысл математического ожидания:

Математическое ожидание приблизительно равно среднему арифметическому наблюдаемых значений случайной величины:

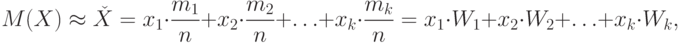
где:

m_k – частота наблюдений, W_k – относительная частота.

Дисперсия и среднее квадратичное отклонение – это числовые характеристики случайной величины, которые позволяют оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания.

Отклонением называют разность между значением случайной величины и ее математическим ожиданием, т. е.

xI - M(X).

Пусть закон распределения дискретной случайной величины известен:

X   x1   x2  …  xn
P   p1   p2  …  pn

Тогда закон распределения отклонения этой случайной величины имеет вид:

X-M(X)   x1-M(X)   x2-M(X)  …  xn-M(X)
  P         p1       p2     …    pn

Так как одни возможные отклонения положительны, а другие отрицательны, то математическое ожидание отклонения обладает важным свойством:

M(X – M(X))=0,

т.е. математическое ожидание отклонения всегда равно нулю.

Поэтому для оценки рассеяния случайной величины вокруг ее математического ожидания вычисляют квадрат отклонения случайной величины, т. е.

(xi - M (X))2.

Дисперсией (рассеянием) случайной величины (как дискретной, так и непрерывной) называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Для дискретной случайной величины: D(X) = M(X – M(X))²

Для непрерывной случайной величины:

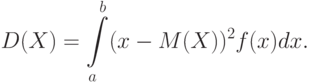
В последнем выражении все возможные значения случайной величины принадлежат отрезку (a, b).

Дисперсия случайной величины (как дискретной, так и случайной) есть неслучайная (постоянная величина).

Пример:

Дискретная случайная величина имеет следующий закон распределения:

X    1     2     5
P   0.3   0.5   0.2

Математическое ожидание этой случайной величины:

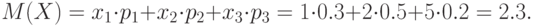
Квадраты отклонений возможных значений случайной величины:

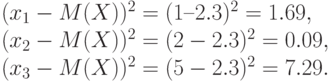
Закон распределения квадрата отклонения:

(x-M(X))2   1.69   0.09   7.29
p           0.3    0.5    0.2

Тогда дисперсия приведенной случайной величины равна:

Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии, т. е.

В приведенном примере среднее квадратичное отклонение случайной величины равно:

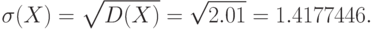
Для вычисления дисперсии часто бывает удобно пользоваться следующей формулой: D(X)=M(X²)–(M(X))², т. е. дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.

Рассмотрим еще раз предыдущий пример.

Дискретная случайная величина задана законом распределения:

X   1     2     5
P  0.3   0.5   0.2

Математическое ожидание этой случайной величины равно:

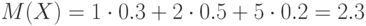
Закон распределения квадрата случайной величины, т. е. X²:

X2   1     4     25
P   0.3   0.5   0.2

Математическое ожидание X² равно:

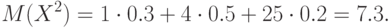
Тогда дисперсия приведенной случайной величины равна: