Индуктивные определения и степени
Мы определили сложение и умножение ординалов с помощью явных конструкций порядка на соответствующих множествах. Вместо этого можно было бы их определить индуктивно.
Теорема 38.Сложение ординалов обладает следующими свойствами:
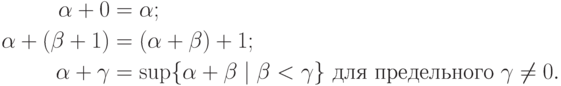
Доказательство. Два первых свойства очевидны; проверим третье.
Если 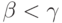 ,
то
,
то 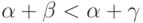 , так что
, так что  будет
верхней
границей всех сумм вида
будет
верхней
границей всех сумм вида  при
при 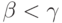 .
Надо проверить, что эта граница точная. Пусть некоторый
ординал
.
Надо проверить, что эта граница точная. Пусть некоторый
ординал  меньше
меньше  . Убедимся, что он
меньше
. Убедимся, что он
меньше  для некоторого
для некоторого 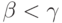 . Если
. Если 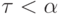 ,
все очевидно.
Если
,
все очевидно.
Если  , представим его в виде
, представим его в виде 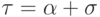 .
Тогда
.
Тогда 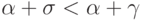 и
потому
и
потому 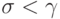 .
Поскольку ординал
.
Поскольку ординал  предельный,
предельный,  также меньше
также меньше  и остается положить
и остается положить  .
.
Указанные свойства однозначно определяют операцию сложения, так
как представляют собой рекурсивное определение по  (если
есть две операции сложения, обладающие этими свойствами, возьмем
минимальное
(если
есть две операции сложения, обладающие этими свойствами, возьмем
минимальное  , для которого они различаются и т.д).
, для которого они различаются и т.д).
Аналогично можно определить и умножение:
Теорема 39. Умножение ординалов обладает следующими свойствами:

Доказательство.
Доказательство аналогично, нужно только проверить, что
если  для предельного
для предельного  , то
, то 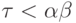 для некоторого
для некоторого 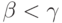 .
Как мы видели на с.101,
ординал
.
Как мы видели на с.101,
ординал  имеет вид
имеет вид 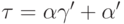 при
при  ; достаточно
положить
; достаточно
положить  .
.
Возникает естественное желание определить операцию
возведения в степень. Мы уже по
существу определили
возведение в целую положительную степень ( 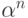 есть
произведение
есть
произведение  сомножителей, равных
сомножителей, равных  ).
Другими словами, если
).
Другими словами, если  упорядочено по
типу
упорядочено по
типу  , то множество
, то множество 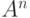 последовательностей
длины
последовательностей
длины  с элементами из
с элементами из  с обратным лексикографическим порядком
(сравнение справа налево) упорядочено по типу
с обратным лексикографическим порядком
(сравнение справа налево) упорядочено по типу 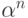 .
.
Следующий шаг- определить 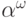 . Первая идея,
приходящая в голову- взять множество
. Первая идея,
приходящая в голову- взять множество 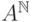 бесконечных
последовательностей и определить на нем полный порядок. Но
как его ввести- неясно. Поэтому можно попробовать
определить возведение в степень
индуктивно
с помощью
следующих соотношений:
бесконечных
последовательностей и определить на нем полный порядок. Но
как его ввести- неясно. Поэтому можно попробовать
определить возведение в степень
индуктивно
с помощью
следующих соотношений:
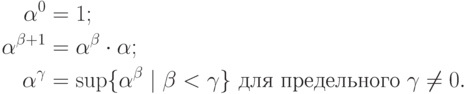
Замечание. Тут опять мы подходим к опасной границе парадоксов и вынуждены выражаться уклончиво. На самом деле теорема о трансфинитной рекурсии говорила об определении функции на вполне упорядоченном множестве, а ординалы не образуют множества- их слишком много. Кроме того, в ней шла речь о функциях со значениями в некотором заданном множестве, которого здесь тоже нет. Подобные индуктивные определения можно корректно обосновать в теории множеств с использованием так называемой аксиомы подстановки, но мы об этом говорить не будем. Вместо этого мы дадим явное описание возведения в степень, свободное от этих проблем.
Чтобы понять смысл возведения в степень, посмотрим, как выглядит
ординал 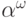 (для некоторого
(для некоторого  ). Пусть
). Пусть  -
множество, упорядоченное по типу
-
множество, упорядоченное по типу  .
Ординал
.
Ординал 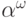 по определению есть точная верхняя грань
по определению есть точная верхняя грань 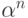 для
натуральных
для
натуральных  . Ординал
. Ординал 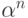 есть
порядковый тип множества
есть
порядковый тип множества 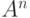 , упорядоченного в обратном
лексикографическом порядке. Чтобы найти точную верхнюю грань,
представим множества
, упорядоченного в обратном
лексикографическом порядке. Чтобы найти точную верхнюю грань,
представим множества 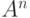 как начальные отрезки друг друга.
Например,
как начальные отрезки друг друга.
Например, 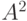 состоит из пар
состоит из пар 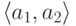 и
отождествляется с начальным отрезком в
и
отождествляется с начальным отрезком в 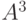 , состоящим из
троек
, состоящим из
троек 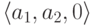 . (Здесь
. (Здесь  -
наименьший элемент
в
-
наименьший элемент
в  .) Теперь видно, что все множества
.) Теперь видно, что все множества 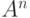 можно
рассматривать как
начальные отрезки множества
можно
рассматривать как
начальные отрезки множества 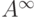 , состоящего из бесконечных
последовательностей
, состоящего из бесконечных
последовательностей 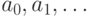 , элементы которых
принадлежат
, элементы которых
принадлежат  и в которых лишь конечное число членов отлично
от нуля. (Последнее требование делает корректным определение
обратного лексикографического порядка- мы находим самую правую
позицию, в которой последовательности различаются, и сравниваем
их значения в этой позиции.) В объединении эти начальные отрезки
дают все
и в которых лишь конечное число членов отлично
от нуля. (Последнее требование делает корректным определение
обратного лексикографического порядка- мы находим самую правую
позицию, в которой последовательности различаются, и сравниваем
их значения в этой позиции.) В объединении эти начальные отрезки
дают все 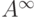 , так что это множество с описанным порядком
имеет тип
, так что это множество с описанным порядком
имеет тип 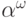 .
.
Аналогичное утверждение верно и для любого показателя степени.
Пусть  и
и  - вполне упорядоченные множества,
имеющие порядковые
типы
- вполне упорядоченные множества,
имеющие порядковые
типы  и
и  . Рассмотрим
множество
. Рассмотрим
множество ![[B\to A]](/sites/default/files/tex_cache/dbea59e56a8b322788914be99997bd18.png) состоящее из отображений
состоящее из отображений  в
в  , имеющих " конечный
носитель" (равных минимальному
элементу
, имеющих " конечный
носитель" (равных минимальному
элементу  всюду, за
исключением конечного множества). Введем на
всюду, за
исключением конечного множества). Введем на ![[B\nolinebreak\to A]](/sites/default/files/tex_cache/4ff5b5a5d06cd533d504d2eca60a948f.png) порядок: если
порядок: если 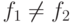 , выберем наибольший
элемент
, выберем наибольший
элемент 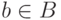 ,
для которого
,
для которого 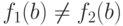 и сравним
и сравним 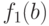 и
и 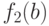 .
.
