Множества
Множества
Основные понятия и обозначения, связанные с множествами и операциями над ними:
-
Множества состоят из элементов.
Запись
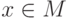 означает, что
означает, что  является элементом
множества
является элементом
множества  .
. - Говорят, что множество
 является подмножеством
множества
является подмножеством
множества  (запись:
(запись:  ),
если все элементы
),
если все элементы  являются элементами
являются элементами  .
. - Множества
 и
и  равны
(запись:
равны
(запись: 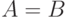 ), если они
содержат одни и те же элементы (другими словами, если
), если они
содержат одни и те же элементы (другими словами, если  и
и 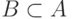 ).
). - Если
 - подмножество
- подмножество  , не равное
всему
, не равное
всему  , то
, то  называют собственным подмножеством
называют собственным подмножеством  (запись:
(запись: 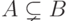 ).
). -
Пустое
множество
 не содержит ни одного
элемента и является подмножеством любого множества.
не содержит ни одного
элемента и является подмножеством любого множества. -
Пересечение
 двух множеств
двух множеств  и
и  состоит из элементов, которые принадлежат обоим множествам
состоит из элементов, которые принадлежат обоим множествам  и
и  . Это записывают так:(читается: множество таких
. Это записывают так:(читается: множество таких
 , что
, что  ).
). -
Объединение
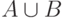 состоит из элементов, которые
принадлежат хотя
бы одному из множеств
состоит из элементов, которые
принадлежат хотя
бы одному из множеств  и
и  :
:
-
Разность
 состоит из элементов, которые
принадлежат
состоит из элементов, которые
принадлежат  , но
не принадлежат
, но
не принадлежат  :Если множество
:Если множество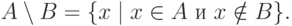
 является подмножеством
множества
является подмножеством
множества  , разность
, разность  называют также дополнением
называют также дополнением  до
до  .
. -
Симметрическая разность
 состоит из
элементов, которые принадлежат ровно одному из множеств
состоит из
элементов, которые принадлежат ровно одному из множеств  и
и  :
: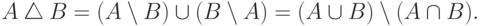
- Через
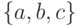 обозначается
множество, которое содержит элементы
обозначается
множество, которое содержит элементы  ,
,  ,
,  и не содержит других.
Если среди
и не содержит других.
Если среди  ,
,  ,
,  есть равные,
оно может содержать один
или два элемента. Подобное
обозначение используется и в менее формальных ситуациях:
множество членов последовательности
есть равные,
оно может содержать один
или два элемента. Подобное
обозначение используется и в менее формальных ситуациях:
множество членов последовательности 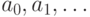 обозначается
обозначается 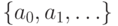 или даже
или даже 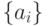 . Более
аккуратная запись для
того же множества такова:
. Более
аккуратная запись для
того же множества такова: 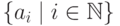 , где
, где  - множество натуральных чисел
- множество натуральных чисел 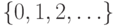 .
.
Понятие множества появилось в математике сравнительно недавно, в
конце 19-го века, в связи с работами Кантора
(сравнение
мощностей множеств), о которых пойдет речь дальше.
Некоторое время назад этот язык пытались внедрить в школьное преподавание,
объясняя ученикам, что у уравнения 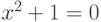 есть множество
решений (впрочем, пустое), что множество решений системы
уравнений есть пересечение множеств решений каждого из них (а
для "совокупности" уравнений - объединение), что в
множестве
есть множество
решений (впрочем, пустое), что множество решений системы
уравнений есть пересечение множеств решений каждого из них (а
для "совокупности" уравнений - объединение), что в
множестве  не три элемента, а два, и оно равно
множеству
не три элемента, а два, и оно равно
множеству 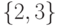 , что
, что  ,
,  и
и 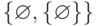 - это три совершенно разных
множества и т.д. Но все равно большинство школьников так и не
поняло, почему множество решений уравнения
- это три совершенно разных
множества и т.д. Но все равно большинство школьников так и не
поняло, почему множество решений уравнения  можно
записывать как
можно
записывать как 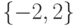 , а множество решений уравнения
, а множество решений уравнения  нельзя записывать как
нельзя записывать как  (а
надо писать
(а
надо писать  ). Отметим кстати еще два расхождения: в школе
натуральные числа начинаются с единицы, а в некоторых
книжках - с нуля (мы тоже будем называть нуль натуральным
числом). Кроме того, иногда вместо
). Отметим кстати еще два расхождения: в школе
натуральные числа начинаются с единицы, а в некоторых
книжках - с нуля (мы тоже будем называть нуль натуральным
числом). Кроме того, иногда вместо  пишут
пишут  ,
используя
,
используя  для собственных подмножеств (вместо
нашего
для собственных подмножеств (вместо
нашего  ).
).
Мы предполагаем, что перечисленные выше основные понятия теории множеств более или менее вам знакомы, и будем достаточно свободно ими пользоваться. Вот несколько задач для самоконтроля; надеемся, что большинство из них не представит для вас большого труда.
1.Старейший математик среди шахматистов и старейший шахматист среди математиков - это один или тот же человек или (возможно) разные?
2. Лучший математик среди шахматистов и лучший шахматист среди математиков - это один или тот же человек или (возможно) разные?
3. Каждый десятый математик - шахматист, а каждый шестой шахматист - математик. Кого больше - математиков или шахматистов - и во сколько раз?
4. Существуют ли такие множества  ,
,  и
и  ,
что
,
что 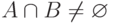 ,
,  и
и 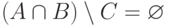 ?
?
5. Какие из равенств
(а) 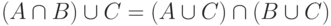 ;
(б)
;
(б) 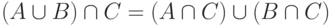 ;
(в)
;
(в)  ;
(г)
;
(г)  ;
(д)
;
(д) 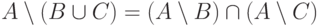 ;
(е)
;
(е) 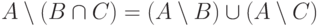 верны для любых множеств
верны для любых множеств 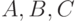 ?
?
6. Проведите подробное доказательство верных равенств предыдущей
задачи, исходя из определений. (Докажем, что множества в левой и
правой частях равны. Пусть  - любой элемент левой части
равенства. Тогда... Поэтому
- любой элемент левой части
равенства. Тогда... Поэтому  входит в правую часть.
Обратно, пусть...) Приведите контрпримеры к неверным
равенствам.
входит в правую часть.
Обратно, пусть...) Приведите контрпримеры к неверным
равенствам.
7. Докажите, что симметрическая разность ассоциативна: 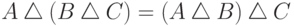 для любых
для любых  ,
,  и
и  . (Указание: сложение
по модулю
. (Указание: сложение
по модулю  ассоциативно.)
ассоциативно.)
8. Докажите, что 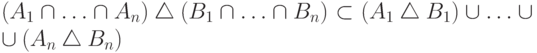 для любых
множеств
для любых
множеств  и
и  .
.
9.Докажите, что если какое-то равенство (содержащее переменные для
множеств и операции  ,
,  ,
, 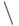 ) неверно, то можно
найти контрпример к нему, в котором множества пусты или состоят
из одного элемента.
) неверно, то можно
найти контрпример к нему, в котором множества пусты или состоят
из одного элемента.
10. Сколько различных выражений для множеств можно составить из
переменных  и
и  с помощью (многократно используемых)
операций пересечения, объединения и разности? (Два выражения
считаются одинаковыми, если они равны при любых значениях
переменных.) Тот же вопрос для трех множеств и для
с помощью (многократно используемых)
операций пересечения, объединения и разности? (Два выражения
считаются одинаковыми, если они равны при любых значениях
переменных.) Тот же вопрос для трех множеств и для  множеств.
(Ответ в общем случае:
множеств.
(Ответ в общем случае:  .)
.)
11. Тот же вопрос, если используются только операции  и
и  .
(Для двух и трех переменных это число несложно подсчитать,
но общей формулы для
.
(Для двух и трех переменных это число несложно подсчитать,
но общей формулы для  переменных не известно. Эту
задачу называют также задачей о
числе монотонных булевых функций
от
переменных не известно. Эту
задачу называют также задачей о
числе монотонных булевых функций
от  аргументов.)
аргументов.)
12. Сколько существует подмножеств у  - элементного множества?
- элементного множества?
13. Пусть множество  содержит
содержит  элементов, а его
подмножество
элементов, а его
подмножество  содержит
содержит  элементов. Сколько
существует
множеств
элементов. Сколько
существует
множеств  , для которых
, для которых 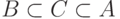 ?
?
14. Множество  содержит
содержит  элементов. В нем выделено
элементов. В нем выделено  подмножеств,
причем ни одно из них не является подмножеством
другого. Каково может быть максимальное значение числа
подмножеств,
причем ни одно из них не является подмножеством
другого. Каково может быть максимальное значение числа  ?
(Указание. Максимум достигается, когда все подмножества имеют
по
?
(Указание. Максимум достигается, когда все подмножества имеют
по  элементов. В самом деле, представим себе, что мы начинаем
с пустого множества и добавляем по одному элементу, пока не получится
множество
элементов. В самом деле, представим себе, что мы начинаем
с пустого множества и добавляем по одному элементу, пока не получится
множество  . В ходе такого процесса может появиться не
более одного выделенного множества; с другой стороны, можно
подсчитать математическое ожидание числа выделенных множеств по
линейности; вероятность пройти через данное множество
. В ходе такого процесса может появиться не
более одного выделенного множества; с другой стороны, можно
подсчитать математическое ожидание числа выделенных множеств по
линейности; вероятность пройти через данное множество 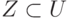 минимальна, когда
минимальна, когда  содержит
содержит  элементов,
поскольку все множества данного размера равновероятны.)
элементов,
поскольку все множества данного размера равновероятны.)
