Ультрафильтры и компактность
Теорема 86. Множество 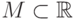 компактно
тогда и только тогда, когда любой элемент множества
компактно
тогда и только тогда, когда любой элемент множества 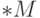 бесконечно близок
к некоторому (стандартному) элементу множества
бесконечно близок
к некоторому (стандартному) элементу множества  .
.
В самом деле, ограниченность означает, что любой элемент
множества  конечен, то есть бесконечно близок к стандартному числу, а замкнутость
позволяет заключить, что это число принадлежит
конечен, то есть бесконечно близок к стандартному числу, а замкнутость
позволяет заключить, что это число принадлежит  .
.
186. Используя полученные только что критерии, покажите,
что любой отрезок ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) действительной прямой
компактен, а любой интервал
действительной прямой
компактен, а любой интервал  открыт.
открыт.
187. Покажите, используя нестандартный критерий открытости, что объединение любого числа открытых множеств открыто. (Напоминание: гипердействительный аналог объединения может не совпадать с объединением гипердействительных аналогов!)
188. Покажите, что пересечение двух (или любого конечного числа) открытых множеств открыто. (Где используется конечность?)
189. Докажите, что последовательность фундаментальна тогда и только тогда, когда любые два ее бесконечных члена бесконечно близки (предварительно уточнив формулировку этого утверждения).
190. Докажите, что всякая фундаментальная последовательность сходится, используя приведенный критерий фундаментальности. (Указание. Ограниченность приходится доказывать, исходя из стандартных определений.)
191. Докажите, что если последовательность ограничена и имеет единственную предельную точку, то она сходится (к этой точке).
192. Докажите, что ограниченная возрастающая последовательность имеет предел.
Перейдем к функциям действительного переменного и дадим нестандартное определение предела (аналогичное приведенному выше для последовательностей).
Теорема 87. Число 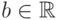 есть предел функции
есть предел функции 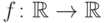 в
точке
в
точке 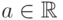 тогда и только тогда, когда
тогда и только тогда, когда 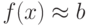 для всех
для всех  , бесконечно близких к
, бесконечно близких к  , но
отличных от
, но
отличных от  .
.
Пусть функция  имеет предел
имеет предел  согласно
согласно  -
- 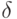 -определению и для всякого
-определению и для всякого 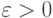 найдется
найдется 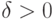 с нужными свойствами. Бесконечно близкое к
с нужными свойствами. Бесконечно близкое к  число
число  попадает в
попадает в 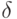 -окрестность
точки
-окрестность
точки  при любом стандартном
при любом стандартном 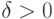 , поэтому
, поэтому  попадает в
попадает в  -окрестность точки
-окрестность точки  .
.
Напротив, если при некотором  для любого
для любого 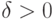 найдется точка
найдется точка  , для которой
, для которой  , но
, но  , то можно применить принцип переноса
(для данного стандартного
, то можно применить принцип переноса
(для данного стандартного  ) и взять бесконечно
малое
) и взять бесконечно
малое 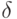 .
.
Непосредственным следствием является нестандартный критерий
непрерывности: функция 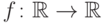 непрерывна
в (стандартной) точке
непрерывна
в (стандартной) точке  тогда и только тогда, когда
тогда и только тогда, когда 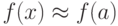 для всех
для всех  , бесконечно близких к
, бесконечно близких к  .
.
Для функции, определенной на некотором множестве 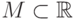 , критерий непрерывности в точке
, критерий непрерывности в точке  выглядит так:
выглядит так: 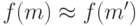 для всякой точки
для всякой точки 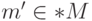 , бесконечно близкой к
, бесконечно близкой к  .
.
193. Проверьте это.
Поучительно понять, чем это свойство отличается от равномерной непрерывности.
Теорема 88. Функция 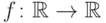 равномерно непрерывна
на множестве
равномерно непрерывна
на множестве 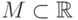 тогда и только тогда, когда для всех
тогда и только тогда, когда для всех  выполнено
выполнено  .
.
Пусть выполнено обычное  -
- 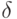 -
определение непрерывности. Бесконечно близкие точки
-
определение непрерывности. Бесконечно близкие точки 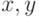 отличаются
менее чем на (стандартное)
отличаются
менее чем на (стандартное) 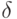 , а потому их образы
отличаются менее чем на
, а потому их образы
отличаются менее чем на  . Это верно для любого
стандартного
. Это верно для любого
стандартного  , поэтому
, поэтому 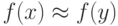 .
.
Обратно, если функция не является равномерно непрерывной, то для
некоторого  и для любого
и для любого 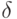 найдутся
точки, отстоящие менее чем на
найдутся
точки, отстоящие менее чем на 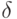 , образы которых отстоят более
чем на
, образы которых отстоят более
чем на  . Остается применить при данном
. Остается применить при данном  принцип переноса и взять бесконечно
малое
принцип переноса и взять бесконечно
малое 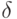 .
.
Чем это отличается от непрерывности во всех точках
множества  ? Непрерывность во всех точках
? Непрерывность во всех точках  означает, что для любого стандартного
означает, что для любого стандартного  и любого бесконечно близкого
к нему
и любого бесконечно близкого
к нему  мы имеем
мы имеем  .
Отсюда следует, что для любых
.
Отсюда следует, что для любых 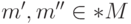 , бесконечно
близких к некоторому стандартному
, бесконечно
близких к некоторому стандартному  , выполнено
, выполнено 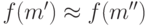 . Но в множестве
. Но в множестве 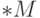 могут
быть бесконечно близкие элементы, стандартная часть которых не лежит
в
могут
быть бесконечно близкие элементы, стандартная часть которых не лежит
в  (или вообще не имеющие стандартной части, то есть
бесконечные). Легко понять, что для компактного
(или вообще не имеющие стандартной части, то есть
бесконечные). Легко понять, что для компактного  такого быть
не может (стандартная часть любого элемента
такого быть
не может (стандартная часть любого элемента 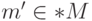 принадлежит
принадлежит  согласно теореме 86).
Тем самым мы получили (почти что тривиальное) нестандартное
доказательство классической теоремы: непрерывная на компакте
функция равномерно непрерывна.
согласно теореме 86).
Тем самым мы получили (почти что тривиальное) нестандартное
доказательство классической теоремы: непрерывная на компакте
функция равномерно непрерывна.
Вот еще несколько "нестандартных" доказательств стандартных (во всех смыслах этого слова) теорем из курса математического анализа.
Теорема 89. Непрерывная на отрезке функция, принимающая значения разных знаков на концах отрезка, имеет нуль на этом отрезке.
Разделим отрезок на  равных частей. Среди них найдется часть,
на которой функция меняет знак. По принципу переноса и при
делении отрезка на бесконечное гипернатуральное число частей
найдется часть, на которой функция меняет знак. Но концы этой
части бесконечно близки к некоторой стандартной точке отрезка.
Эта точка будет нулем функции (если в ней функция, скажем,
положительна, то по непрерывности в бесконечно близких к ней
концах отрезка изменения знака функция будет положительной).
равных частей. Среди них найдется часть,
на которой функция меняет знак. По принципу переноса и при
делении отрезка на бесконечное гипернатуральное число частей
найдется часть, на которой функция меняет знак. Но концы этой
части бесконечно близки к некоторой стандартной точке отрезка.
Эта точка будет нулем функции (если в ней функция, скажем,
положительна, то по непрерывности в бесконечно близких к ней
концах отрезка изменения знака функция будет положительной).
Теорема 90. Непрерывная во всех точках компакта функция ограничена на нем.
Пусть функция  непрерывна на компакте
непрерывна на компакте  . Следуя
нестандартному критерию ограниченности, мы должны показать, что
значения функции
. Следуя
нестандартному критерию ограниченности, мы должны показать, что
значения функции 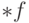 во всех точках
во всех точках 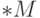 конечны. Но всякая точка
конечны. Но всякая точка 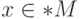 бесконечно близка к некоторой
стандартной точке
бесконечно близка к некоторой
стандартной точке 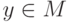 (компактность), а потому
(компактность), а потому  (непрерывность),
поэтому
(непрерывность),
поэтому 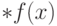 конечно.
конечно.
Обратите внимание, что мы пользовались аксиомой полноты (для
множества  ) только один раз, при доказательстве
теоремы 78. Это и не удивительно, поскольку из
утверждения этой теоремы следует аксиома полноты.
) только один раз, при доказательстве
теоремы 78. Это и не удивительно, поскольку из
утверждения этой теоремы следует аксиома полноты.
194. Убедитесь в этом, следуя такой схеме. Пусть  — произвольное
ограниченное множество действительных чисел. Покажите (стандартными
рассуждениями), что для любого
— произвольное
ограниченное множество действительных чисел. Покажите (стандартными
рассуждениями), что для любого  найдется число
найдется число  , являющееся верхней гранью, для которого
, являющееся верхней гранью, для которого  не будет верхней гранью. Примените
принцип переноса, взяв бесконечно малое
не будет верхней гранью. Примените
принцип переноса, взяв бесконечно малое  и
рассмотрев стандартную часть соответствующего числа
и
рассмотрев стандартную часть соответствующего числа  .
.
195. Докажите, что производная стандартной функции 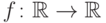 в стандартной точке
в стандартной точке  равна
стандартному числу
равна
стандартному числу  тогда и только тогда, когда
тогда и только тогда, когда 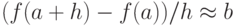 для всех бесконечно малых
для всех бесконечно малых 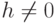 .
.
196. Покажите, что  согласно нестандартному
определению производной (предыдущая задача).
согласно нестандартному
определению производной (предыдущая задача).
197. Как использовать нестандартный анализ для определения понятия интеграла?
В наших примерах все рассмотрения были ограничены множеством гипердействительных чисел. Это ограничение кажется существенным — не вполне ясно, каким образом можно применить те же методы к произвольному топологическому пространству (в котором нет бесконечно больших чисел). Тем не менее это возможно, и об этом можно прочесть в книгах Дэвиса [11] или Успенского [27].
