Ультрафильтры и компактность
Теорема 78. Всякое конечное гипердействительное число бесконечно близко к некоторому стандартному числу.
(Заметим, что обратное утверждение очевидно: всякое
гипердействительное число, бесконечно близкое к некоторому
стандартному  , конечно, поскольку содержится между
стандартными числами
, конечно, поскольку содержится между
стандартными числами 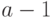 и
и  .)
.)
Пусть  — конечное гипердействительное число. Рассмотрим
множество множество
— конечное гипердействительное число. Рассмотрим
множество множество  всех стандартных действительных чисел,
меньших или равных
всех стандартных действительных чисел,
меньших или равных  , а также множество
, а также множество  всех
стандартных действительных чисел, больших или равных
всех
стандартных действительных чисел, больших или равных  .
Конечность числа
.
Конечность числа  гарантирует, что оба этих множества
непусты (если бы, скажем,
гарантирует, что оба этих множества
непусты (если бы, скажем,  было пусто, то
было пусто, то  было бы положительным бесконечно большим). Заметим, что
было бы положительным бесконечно большим). Заметим, что  и
и  не пересекаются (если только
не пересекаются (если только  само не является стандартным,
и тогда доказывать нечего) и в объединении дают все
само не является стандартным,
и тогда доказывать нечего) и в объединении дают все  .
.
По аксиоме полноты существует действительное число  , для
которого
, для
которого 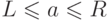 . Покажем, что
. Покажем, что  бесконечно мало. Проверим, например, что для любого стандартного
бесконечно мало. Проверим, например, что для любого стандартного 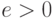 выполнено неравенство
выполнено неравенство  , то есть
, то есть 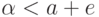 . Это понятно: если
. Это понятно: если 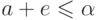 , то
, то 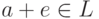 , что противоречит свойству
, что противоречит свойству 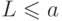 . По аналогичным
причинам
. По аналогичным
причинам 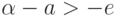 .
.
Стандартное число  , бесконечно близкое к конечному
гипердействительному
, бесконечно близкое к конечному
гипердействительному  , называется стандартной
частью числа
, называется стандартной
частью числа  . Стандартная часть определена однозначно,
так как два разных стандартных числа не могут быть бесконечно
близки к одному и тому же гипердействительному числу (тогда бы
они были близки друг к другу, что невозможно). Поэтому можно
ввести обозначение
. Стандартная часть определена однозначно,
так как два разных стандартных числа не могут быть бесконечно
близки к одному и тому же гипердействительному числу (тогда бы
они были близки друг к другу, что невозможно). Поэтому можно
ввести обозначение 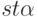 для стандартной части конечного
числа
для стандартной части конечного
числа  .
.
174. Докажите, что если  и
и  конечны, причем
конечны, причем  , то и
, то и 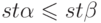 .
.
Теорема 79. Среди гипердействительных чисел есть ненулевые бесконечно малые, а также бесконечно большие числа.
Напомним, что по нашему предположению  не совпадает с
не совпадает с  , то есть существует некоторое нестандартное
гипердействительное число
, то есть существует некоторое нестандартное
гипердействительное число  . Если
. Если  бесконечно, то
бесконечно, то  — искомое ненулевое бесконечно малое число. Если
— искомое ненулевое бесконечно малое число. Если  конечно, то
конечно, то  — искомое
ненулевое бесконечно малое число (а обратное к нему будет бесконечно
большим).
— искомое
ненулевое бесконечно малое число (а обратное к нему будет бесконечно
большим).
Заметим, что при построении гипердействительных чисел с помощью
формул  (для новой константы
(для новой константы  и всех
стандартных
и всех
стандартных  ) и теоремы компактности существование бесконечно больших элементов
очевидно: таковым будет значение этой самой константы
) и теоремы компактности существование бесконечно больших элементов
очевидно: таковым будет значение этой самой константы  .
.
Теперь обратимся к натуральным и целым числам.
Теорема 80. Существуют нестандартные гипернатуральные числа, при этом все они бесконечно велики.
(Таким образом, для гипернатуральных чисел конечность и стандартность равносильны.)
Всякое положительное действительное число есть сумма
натурального и числа из 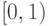 . Принцип переноса гарантирует,
что всякое положительное гипердействительное число
. Принцип переноса гарантирует,
что всякое положительное гипердействительное число  есть
сумма гипернатурального
есть
сумма гипернатурального  и гипердействительного
и гипердействительного  , для которого
, для которого 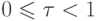 . Возьмем
. Возьмем  бесконечно
большим, тогда и
бесконечно
большим, тогда и  будет бесконечно большим. Первое утверждение
доказано.
будет бесконечно большим. Первое утверждение
доказано.
Пусть теперь  — конечное гипернатуральное число. По
определению конечности оно меньше некоторого стандартного числа
— конечное гипернатуральное число. По
определению конечности оно меньше некоторого стандартного числа  ,
скажем, числа
,
скажем, числа 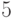 . Но в стандартной модели верна формула
. Но в стандартной модели верна формула
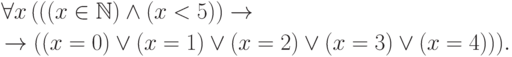
 , поэтому число
, поэтому число  совпадает с одним из стандартных чисел
совпадает с одним из стандартных чисел 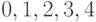 .
.175. Покажите, что для всякого гипердействительного числа существует большее его гипернатуральное.
176. Рассмотрим гипернатуральные числа как упорядоченное множество.
Покажите, что оно изоморфно 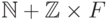 , где
, где  — плотное линейно упорядоченное множество без первого
и последнего элементов. (Порядок на
— плотное линейно упорядоченное множество без первого
и последнего элементов. (Порядок на  : сравниваются
сначала вторые элементы, а при равенстве — первые.)
: сравниваются
сначала вторые элементы, а при равенстве — первые.)
Гипернатуральные числа позволяют говорить о бесконечно далеких
членах (стандартных) последовательностей действительных чисел.
Пусть 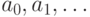 — такая последовательность. Рассмотрим ее
график, то есть множество пар
— такая последовательность. Рассмотрим ее
график, то есть множество пар 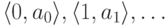 , как двуместный предикат. Утверждение о том,
что этот предикат задает график функции, определенной на
натуральных числах, можно записать в виде формулы. Принцип
переноса гарантирует, что гипердействительный аналог этого
предиката будет функцией, определенной на гипернатуральных
числах и принимающей гипердействительные значения. Значение этой
функции на гипернатуральном числе
, как двуместный предикат. Утверждение о том,
что этот предикат задает график функции, определенной на
натуральных числах, можно записать в виде формулы. Принцип
переноса гарантирует, что гипердействительный аналог этого
предиката будет функцией, определенной на гипернатуральных
числах и принимающей гипердействительные значения. Значение этой
функции на гипернатуральном числе  можно обозначать
можно обозначать 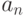 , не опасаясь путаницы (при стандартных
, не опасаясь путаницы (при стандартных  мы получаем одно и то же).
мы получаем одно и то же).
Таким образом, любая последовательность приобретает — помимо своего желания — бесконечный "хвост".
177. Покажите, что если две последовательности отличаются лишь в конечном числе членов, то их бесконечные хвосты одинаковы.
Сейчас мы используем продолжение последовательностей для доказательства такого факта:
