Теории и модели

Теория Th(Z,=,<,S,0)

Что изменится, если мы добавим к сигнатуре, помимо прибавления единицы, еще и отношение порядка? Как мы видели (см. доказательство теоремы 29 и задачу после него), элиминация кванторов по-прежнему возможна. Для придания законности нам нужны такие свойства интерпретации (которую мы предполагаем нормальной): она представляет собой линейно упорядоченное множество, в котором каждый элемент имеет непосредственно следующий (совпадающий с значением функции ) и непосредственно предшествующий. В отличие от предыдущего примера, нам достаточно конечного набора аксиом. Таким образом, теория конечно аксиоматизируема, а также (как и в предыдущем примере) полна, разрешима, но не категорична в счетной мощности.

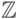Можно обойтись и без элиминации кванторов, рассуждая иначе. Рассмотрим теорию линейно упорядоченных множеств со следующим и предыдущим элементом и опишем все ее модели. Именно, мы покажем, что любая нормальная модель этой теории имеет вид , где — произвольное линейно упорядоченное множество (порядок на парах таков: сначала сравниваются -компоненты, а в случае равенства — -компоненты.) В самом деле, будем говорить, что элементы и лежат "в одной галактике", если между ними конечное число элементов. (Легко проверить, что это действительно отношение эквивалентности, и наше множество разбивается на галактики.) Далее проверяем, что каждая галактика изоморфна 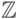(как упорядоченное множество) и что на галактиках естественно определяется порядок.

Теперь с помощью игры Эренфойхта (см. раздел "Элементарная эквивалентность", теорема 37) мы показываем, что все нормальные модели этой теории элементарно эквивалентны. Отсюда заключаем, что теория полна (как в доказательстве теоремы 65, где мы по существу использовали элементарную эквивалентность моделей, а не их изоморфизм).

126. Покажите, что теория 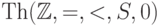не категорична ни в какой несчетной мощности.

127. Будет ли теория конечно аксиоматизируемой? разрешимой? категоричной?

128. Будет ли теория 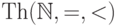конечно аксиоматизируемой? разрешимой? категоричной?

Теория Th(Q,=,<,+,0,1)

Эту теорию мы рассматривали в разделе "Элиминация кванторов". Мы ограничимся двумя константами и , поскольку любую атомарную формулу можно привести к общему знаменателю и получить целые константы, которые можно выразить через и .

Мы хотим указать явно набор аксиом этой теории, то есть множество формул, из которых выводятся все теоремы этой теории и только они. Как и в предыдущих примерах, это можно сделать, проанализировав процесс элиминации кванторов и выявив все использованные при этом свойства интерпретации. (Все рассматриваемые нами интерпретации предполагаются нормальными, а аксиомы равенства изначально включаются в строимую нами теорию.)

Прежде всего, нам важно, что по сложению мы имеем абелеву группу (и является ее нулем). Это позволяет в равенствах переносить члены с одной стороны в другую. Для операций с неравенствами нам надо знать, что порядок является линейным и что он согласован со сложением (то есть что из следует 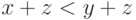). Кроме того, мы умножали равенства и неравенства на рациональные числа. Чтобы это было законно, мы должны знать, что группа является делимой: для всякого уравнения 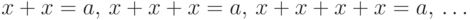имеют решения. (В упорядоченной группе такое решение, как легко показать, единственно.) Наконец, нам надо знать, что .

Кроме этих аксиом (которых счетное число) мы при элиминации ничего не использовали, так что для любой формулы есть бескванторная формула , которая эквивалентна в любой делимой упорядоченной группе. Поэтому любая замкнутая формула, истинная в стандартной интерпретации (в ), истинна в любой делимой упорядоченной группе, и мы получили счетную систему аксиом для теории .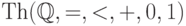

129. Покажите, что эта теория не является конечно аксиоматизируемой. (Указание: делимость любого элемента группы на простое число не вытекает из делимости на все меньшие простые числа — рассмотрим рациональные числа, знаменатель которых взаимно прост с .)

130. Покажите, что эта теория разрешима.

131. Покажите, что эта теория не является категоричной.

132. Покажите, что теория 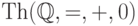не является категоричной в счетной мощности, но категорична в любой несчетной мощности. (Указание: ее модели — векторные пространства над полем рациональных чисел.)

Арифметика Пресбургера

В разделе "Арифметика Пресбургера" мы занимались элиминацией кванторов в теории 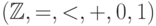, которая потребовала добавления бесконечного числа дополнительных предикатов (сравнимость по модулю для всех целых ).

Проанализировав это рассуждение, можно извлечь из него явную аксиоматизацию для теории 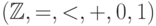(без дополнительных предикатов). Какие свойства порядка и сложения на целых числах мы используем? Нам важно, что целые числа образуют абелеву группу, что порядок согласован со сложением и что 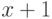есть непосредственно следующий за элемент (достаточно, впрочем, сказать, что непосредственно следует за ). В любой группе можно рассмотреть подгруппу делящихся на элементов (для любой целой константы ) и сравнивать элементы по модулю этой подгруппы. Но этого мало: нам нужно еще иметь возможность делить на с остатком. Это гарантируется такой аксиомой (при каждом — своя аксиома): для любого элемента ровно один из элементов 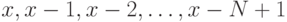делится на .

Можно проверить, что все шаги элиминации кванторов сохраняют равносильность в такой ситуации. Проверим, например, что сравнения можно умножать на целое положительное число. Почему, скажем, равносильно 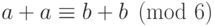? По определению первое означает, что 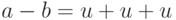для некоторого , а второе — что 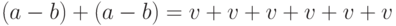для некоторого , и достаточно сослаться на то, что в упорядоченной группе из 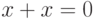следует 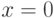(поскольку из следует 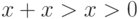). Наиболее сложный шаг — доказательство представительности набора. Здесь надо рассмотреть все случаи расположения произвольного относительно правых частей. В каждом из случаев мы заменяли на первый элемент из окрестности правых частей, встречающийся при движении шагами . Эту процедуру можно понимать как деление расстояния (до ближайшей правой части) на с остатком; возможность этого гарантируется нашими аксиомами.

133. Покажите, что теория 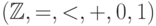разрешима.

134. Покажите, что эта теория не категорична в счетной мощности и опишите все ее счетные модели. (Указание: они имеют вид , где — делимая упорядоченная группа.)

135. Покажите, что эта теория не конечно аксиоматизируема. (Указание: рассмотрите интерпретацию , когда в возможно деление на простые числа, меньшие некоторого , но не на .)