Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Дополнительный материал 1:

Приложение. Параллельные вычисления на кластерах из персональных компьютеров в математической физике (В.Е.Карпов, А.И.Лобанов)
A
|
версия для печати
< Лекция 9 || Дополнительный материал 1: 12345

2. Расчет электрического поля установки РС-20 с использованием кластера из персональных компьютеров

Установка РС-20 была создана в Курчатовском институте и первоначально предназначалась для проведения радиационно-биологических исследований. Необходимость проведения экспериментов по созданию сверхмощных импульсов тока потребовала модернизации для увеличения напряжений и плотности заряда, пропускаемого через плазменный прерыватель тока.

Первоначально эскиз конструкции установки выглядел как спайка двух коаксиальных конденсаторов различного диаметра, внешние обкладки которых соединены металлической поверхностью (рис. 1). В больший конденсатор помещена диэлектрическая вставка, представляющая собой полый усеченный конус. В полиэтиленовую вставку врезаны пары компенсаторных колец. Каждая пара соединена между собой плоскими металлическими кольцами, проходящими через диэлектрик. Внутри всей установки поддерживается вакуум. Внешние обкладки конденсаторов заземлены. На внутренний цилиндрический электрод подается постоянное напряжение. К компенсаторным кольцам подведены постоянные напряжения, увеличивающиеся от нижнего кольца к верхнему. Требуется определить потенциалы и напряженность электрического поля внутри установки, а также оптимальную форму и расположение компенсаторных колец.

Первоначальный эскиз установки RS-20

Рис. 1. Первоначальный эскиз установки RS-20

3. Математическая модель и выбор численного метода

Ввиду осевой симметрии целесообразно перейти в цилиндрическую систему координат ( r, z, \theta ). Распределение потенциала электрического поля \phi описывается уравнением Лапласа:

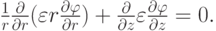$ {\frac{1}{r} \frac{\partial }{\partial r}(\varepsilon r \frac{\partial \varphi} {\partial r}) + \frac{\partial }{\partial z}\varepsilon \frac{\partial \varphi} {\partial z} = 0.} $ ( 6)

На металлических поверхностях значения потенциалов заданы эскизом конструкции. Так как корректно поставить граничные условия на верхнем и нижнем срезе конденсаторов не представляется возможным, будем считать, что конденсаторы продолжаются в обе стороны на бесконечное расстояние. В этом случае на входе и выходе установки получаем граничные условия вида

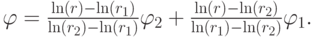$ {\varphi = \frac{{\ln (r) - \ln (r_1 )}}{{\ln (r_2 ) - \ln (r_1 )}}\varphi_2 + \frac{{\ln (r) - \ln (r_2 )}}{{\ln (r_1 ) - \ln (r_2 )}}\varphi_1 .} $ ( 7)

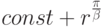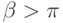Рассматриваемая область не является односвязной (имеются внутренние границы на компенсаторных кольцах). Кроме того, известно, что в плоском случае в окрестности угловых точек решение ведет себя как const + r^{\frac{\pi}{\beta}}, где \beta — величина угла. Для входящих углов, у которых \beta > \pi (в данном случае это точка стыка коаксиальных конденсаторов), производные от решения стремятся к бесконечности как

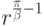
$ r^{\frac{\pi}{\beta}- 1}$
.

Наличие угловой точки предполагает высокие напряженности электрического поля и требует подробных сеток для расчета потенциала. Коэффициент диэлектрической проницаемости среды \varepsilon терпит разрыв на границе раздела сред вакуум — диэлектрик.

Целесообразно использовать для решения поставленной задачи один из явных методов, характеризующихся высокой степенью внутренней параллельности. Применялась пятиточечная разностная аппроксимация, при этом система линейных уравнений решалась итерационным методом Якоби:

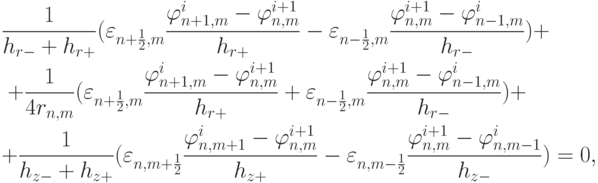\begin{gather*} \frac{1}{{h_{r - } + h_{r + } }}(\varepsilon_{n + \frac{1}{2},m} \frac{{\varphi_{n + 1,m}^{i} - \varphi_{n,m}^{i + 1} }}{{h_{r + } }} - \varepsilon_{n - \frac{1}{2},m}\frac{{\varphi_{n,m}^{i + 1} - \varphi_{n - 1,m}^{i} }}{{h_{r - } }}) + \\ + \frac{1}{{4r_{n,m} }}(\varepsilon_{n + \frac{1}{2},m} \frac{{\varphi_{n + 1,m}^{i} - \varphi_{n,m}^{i + 1} }}{{h_{r + } }} + \varepsilon_{n - \frac{1}{2},m}\frac{{\varphi_{n,m}^{i + 1} - \varphi_{n - 1,m}^{i} }}{{h_{r - } }}) +\\ + \frac{1}{{h_{z - } + h_{z + } }}(\varepsilon_{n,m + \frac{1}{2}} \frac{{\varphi_{n,m + 1}^{i} - \varphi_{n,m}^{i + 1} }}{{h_{z + } }} - \varepsilon_{n,m - \frac{1}{2}} \frac{{\varphi_{n,m}^{i + 1} - \varphi_{n,m - 1}^{i} }}{{h_{z - } }}) = 0, \end{gather*} ( 8)

где верхний индекс указывает на номер итерации. Индексы + и - относятся к величинам шагов сетки справа и сверху от рассматриваемой точки и слева и снизу, соответственно. Для учета разрыва коэффициента диэлектрической проницаемости в качестве значения \varepsilon в полуцелых точках вблизи границы раздела сред выбирались средневзвешенные значения. Использовался следующий критерий выхода из итераций:

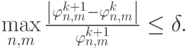$ {\mathop {\max }\limits_{n,m} \frac{{\left| {\varphi_{n,m}^{k + 1} - \varphi_{n,m}^{k} } \right|}}{{\varphi_{n,m}^{k + 1} }} \le \delta .} $ ( 9)
Дальше >>
< Лекция 9 || Дополнительный материал 1: 12345

Вопросы и ответы

вопросов: 0