Синтаксический анализ
Конструирование LR(1)-таблицы
Рассмотрим алгоритм конструирования таблицы, управляющей LR(1) - анализатором.
Пусть G = (N, T, P, S) - КС-грамматика. Пополненной грамматикой для данной грамматики G называется КС- Состояния Action Goto
грамматика

то есть эквивалентная грамматика, в которой введен новый начальный символ S' и новое правило вывода S' -> S.
Это дополнительное правило вводится для того, чтобы определить, когда анализатор должен остановить разбор и зафиксировать допуск входа. Таким образом, допуск имеет место тогда и только тогда, когда анализатор готов осуществить свертку по правилу S' -> S.
LR(1)- ситуацией называется пара ![[A \to \alpha .\beta , a]](/sites/default/files/tex_cache/66069619e2804cbb11fa650f1b1d7da5.png) , где
, где  - правило грамматики, a - терминал или правый
концевой маркер $. Вторая компонента ситуации называется аванцепочкой.
- правило грамматики, a - терминал или правый
концевой маркер $. Вторая компонента ситуации называется аванцепочкой.
Будем говорить, что LR(1)-ситуация ![[A \to \alpha .\beta , a]](/sites/default/files/tex_cache/66069619e2804cbb11fa650f1b1d7da5.png) допустима для активного префикса +, если существует вывод
допустима для активного префикса +, если существует вывод 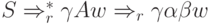 , где
, где  и либо a - первый символ w, либо w = e и a = $.
и либо a - первый символ w, либо w = e и a = $.
Будем говорить, что ситуация допустима, если она допустима для какого-либо активного префикса.
Пример 4.11. Дана грамматика G = ({S, B}, {a, b}, P, S) с правилами
S -> BB
B -> aB | b
Существует правосторонний вывод  .
Легко видеть, что ситуация [B -> a.B, a] допустима для активного
префикса + = aaa, если в определении выше положить
.
Легко видеть, что ситуация [B -> a.B, a] допустима для активного
префикса + = aaa, если в определении выше положить  . Существует также правосторонний
вывод
. Существует также правосторонний
вывод  . Поэтому для активного префикса Baa
допустима ситуация [B -> a.B, $].
. Поэтому для активного префикса Baa
допустима ситуация [B -> a.B, $].
Центральная идея метода заключается в том, что по грамматике строится детерминированный конечный автомат, распознающий активные префиксы. Для этого ситуации группируются во множества, которые и образуют состояния автомата. Ситуации можно рассматривать как состояния недетерминированного конечного автомата, распознающего активные префиксы, а их группировка на самом деле есть процесс построения детерминированного конечного автомата из недетерминированного.
Анализатор, работающий слева-направо по типу сдвиг- свертка, должен уметь распознавать основы на верхушке магазина. Состояние автомата после прочтения содержимого магазина и текущий входной символ определяют очередное действие автомата. Функцией переходов этого конечного автомата является функция переходов LR-анализатора.
Чтобы не просматривать магазин на каждом шаге анализа, на
верхушке магазина всегда хранится то состояние, в котором
должен оказаться этот конечный автомат после того, как он
прочитал символы грамматики в магазине от дна к верхушке.
Рассмотрим ситуацию вида ![[A \to \alpha .B\beta , a]](/sites/default/files/tex_cache/8787945698e66329263c4d4538080363.png) из множества
ситуаций, допустимых для некоторого активного префикса z. Тогда существует правосторонний вывод
из множества
ситуаций, допустимых для некоторого активного префикса z. Тогда существует правосторонний вывод  , где
, где  . Предположим, что из
. Предположим, что из  выводится терминальная строка bw. Тогда для некоторого правила
вывода вида B -> q имеется вывод
выводится терминальная строка bw. Тогда для некоторого правила
вывода вида B -> q имеется вывод  . Таким образом [B -> .q, b] также допустима для z и ситуация
. Таким образом [B -> .q, b] также допустима для z и ситуация ![[A \to \alpha B.\beta , a]](/sites/default/files/tex_cache/02a9a4b768e35adad414abdd44240934.png) допустима для активного префикса zB. Здесь либо b может быть первым терминалом, выводимым из
допустима для активного префикса zB. Здесь либо b может быть первым терминалом, выводимым из 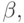 либо из
либо из  выводится e в выводе
выводится e в выводе  и тогда b равно a. То есть b принадлежит
и тогда b равно a. То есть b принадлежит  . Построение всех таких ситуаций для данного множества ситуаций, то есть его
замыкание, делает приведенная ниже функция closure.
. Построение всех таких ситуаций для данного множества ситуаций, то есть его
замыкание, делает приведенная ниже функция closure.
Система множеств допустимых LR(1)-ситуаций для всевозможных активных префиксов пополненной грамматики называется канонической системой множеств допустимых LR(1)-ситуаций. Алгоритм построения канонической системы множеств приведен ниже.
Алгоритм 4.10. Конструирование канонической системы множеств допустимых LR(1)-ситуаций.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Каноническая система C множеств допустимых LR(1)-ситуаций для грамматики G.
Метод. Выполнить для пополненной грамматики G' процедуру items, которая использует функции closure и goto.
function closure(I){ /* I - множество ситуаций */
do{
for (каждой ситуации [A -> alpha.Bbeta, a] из I,
каждого правила вывода B -> gamma из G',
каждого терминала b из FIRST(beta a),
такого, что [B ->.gamma, b] нет в I)
добавить [B ->.gamma, b] к I;
}
while (к I можно добавить новую ситуацию);
return I;
}
function goto(I,X){ /* I - множество ситуаций;
X - символ грамматики */
Пусть J = {[A -> alpha x beta; a] | [A -> alpha.xbeta, a] \in I};
return closure(J);
}
procedure items(G'){ /* G' - пополненная
грамматика */
I' = closure({[S' -> .S, $]});
C = {I0};
do{
for (каждого множества ситуаций I из
системы C, каждого символа грамматики X
такого, что goto(I, X) не пусто
и не принадлежит C)
добавить goto(I, X) к системе C;
}
while (к C можно добавить новое множество
ситуаций);Если I - множество ситуаций, допустимых для некоторого активного префикса +, то goto(I, X) - множество ситуаций, допустимых для активного префикса +X.
Работа алгоритма построения системы C множеств допустимых LR(1)-ситуаций начинается с того, что в C помещается начальное множество ситуаций I0 = closure({[S' -> .S, $]}). Затем с помощью функции goto вычисляются новые множества ситуаций и включаются в C.
По-существу, goto(I, X) - переход конечного автомата из состояния I по символу X.
Рассмотрим теперь, как по системе множеств LR(1)-ситу- аций строится LR(1)-таблица, то есть функции действий и переходов LR(1)-анализатора.
Алгоритм 4.11. Построение LR(1)-таблицы.
Вход. Каноническая система C = {I0, I1, ... , In} множеств допустимых LR(1)-ситуаций для грамматики G.
Выход. Функции Action и Goto, составляющие LR(1)- таблицу для грамматики G.
Метод. Для каждого состояния i функции Action[i, a] и Goto[i, X] строятся по множеству ситуаций Ii:
- Значения функции действия ( Action ) для состояния i
определяются следующим образом:
- если
![[A \rightarrow \alpha .a \beta , b] \in I_i](/sites/default/files/tex_cache/999b6b411c6babe97b122ac4e5ae2ec8.png) (a - терминал) и goto(Ii, a)= Ij, то полагаем Action[i, a] = shift j;
(a - терминал) и goto(Ii, a)= Ij, то полагаем Action[i, a] = shift j;
- если
![[A \rightarrow \alpha; ., a] \in I_i](/sites/default/files/tex_cache/9bcd7335254c949903325ee9a5f25d5c.png) , причем
, причем 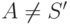 , то полагаем
, то полагаем ![Action[i, a] = reduce A \to \alpha ;](/sites/default/files/tex_cache/22bf5001fed1b57d2f2993b6f664a880.png)
- если
![[S' \rightarrow S., \$] \in I_i](/sites/default/files/tex_cache/51f8d2413db494183dd67bdd6501fd67.png) , то полагаем Action[i, $] = accept.
, то полагаем Action[i, $] = accept.
- если
- Значения функции переходов для состояния i определяются следующим образом: если goto(Ii, A) = Ij, то Goto[i, A] = j (здесь A - нетерминал).
- Все входы в Action и Goto, не определенные шагами 2 и 3, полагаем равными error.
- Начальное состояние анализатора строится из множества, содержащего ситуацию [S' -> .S, $].
Таблица на основе функций Action и Goto, полученных в результате работы алгоритма 4.11., называется канонической LR(1)-таблицей. Работающий с ней LR(1)-анализатор, называется каноническим LR(1)-анализатором.
Пример 4.12. Рассмотрим следующую грамматику, являющуюся пополненной для грамматики из примера 4.8.:
(0) E' -> E
(1) E -> E + T
(2) E -> T
(3) T -> T * F
(4) T -> F
(5) F -> id.
Множества ситуаций и переходы по goto для этой грамматики приведены на рис. 4.9. LR(1)-таблица для этой грамматики приведена на рис. 4.7.
Проследим последовательность создания этих множеств более подробно.
- Вычисляем I0 = closure({[E' -> .E, $]}).
- Ситуация [E' -> .E, $] попадает в него по умолчанию как исходная.
- Если обратиться к обозначениям функции closure, то для
нееЗначит, для терминала $ добавляем ситуации на основе правил со знаком E в левой части правила. Это правила
 и соответствующие им ситуации
и соответствующие им ситуации
![\begin{align*}
& [E \rightarrow. E + T, \$] \text{ и } [E \rightarrow . T, \$]
\end{align*}](/sites/default/files/tex_cache/593a5c1fcbd47126f842ae65257bd2da.png)
- Просматриваем получившиеся ситуации.
Для ситуации [E ->.E + T, $]
 , поэтому
, поэтому  .
На основе этого добавляем к I0 [E -> E + .T, +] и [E ->.T, +].
.
На основе этого добавляем к I0 [E -> E + .T, +] и [E ->.T, +]. - Для ситуации
![[E \to .T, $] \beta = e, first(\beta a) = \{ $\}](/sites/default/files/tex_cache/7c4dd49b8a2e83107958b303f1a7e1a5.png) .
Поэтому добавляем к I0 [T ->. T * F, $] и [T ->.F, $].
.
Поэтому добавляем к I0 [T ->. T * F, $] и [T ->.F, $]. - Подобно этому для ситуации
![[E \to .T, +]\beta = e, first(\beta a) = \{ +\}](/sites/default/files/tex_cache/76cdae16097290c015ac6c186102881b.png) .
Поэтому добавляем к I0 [T ->.T * F, +] и [T ->.F, +].
.
Поэтому добавляем к I0 [T ->.T * F, +] и [T ->.F, +]. - Из ситуации
![[T \to . T * F, +]\beta = *, first(\beta a) = \{ *\}](/sites/default/files/tex_cache/c19c663ddad9197e9fc821a54130f242.png) :
Поэтому добавляем к I0
[T ->.T * F, *] и [T ->.F, *]
:
Поэтому добавляем к I0
[T ->.T * F, *] и [T ->.F, *]
- Далее из ситуации [T ->.F, *] получаем ситуацию [F ->. id, *]. из ситуации [T ->. F, $] - ситуацию [F ->. id, $], а из ситуации [T ->. F, +] - [F ->. id, +].
Таким образом, все 14 искомых ситуаций I0 получены.
Возвращаемся в головную функцию items, включаем I0 в
множество C и исследуем непустые итоги применения функции goto(I0; X), где  .
.
Если посмотреть на вид правил в функции goto(I0; X), то видно, что X должен встретиться в правой части хотя бы одного правила. Для E0 таких правил у нас нет, поэтому значение функции goto(I0, E') пусто.
Возьмем goto(I0; E). E встречается после точки в правых частях двух ситуаций из I0, значит берем эти два правила и переносим в них точки на один символ вправо (пока есть куда - не уперлись в запятую), получаем:
[E' -> E., $]
и
[E -> E. + T, $|+]
Вычислим от каждой из этих ситуаций функцию closure. Но, поскольку справа от точки здесь либо пустая цепочка, либо терминал, то никаких новых ситуаций не возникает. Дальше отслеживаем, может ли куда-то сдвинуться точка дальше на право и по какому символу. Если может, строим соответствующее множество ( рис. 4.9). И т.д.



