Задачи по разделам курса

Языки и их представление

Алфавиты, цепочки и языки

1. Пусть A = {ab, c} и B = {c, ca} - два формальных языка над алфавитом {a, b, c}. Найти следующие формальные языки:
   1. 
   2. A \ B;
   3. A²;
   4. A² \ B²;
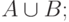
   5. AB.

Представление языков

• Для языка , |x|_b - нечeтное} постройте
  1. Детерминированный конечный автомат;
  2. По нему - регулярное выражение;
  3. По этому выражению - грамматику;
  4. По полученной грамматике перейдите по GN-теореме к N- автомату.

Грамматики

2.3.1. Принадлежит ли цепочка x = abaababb языку, порождаемому грамматикой с правилами:

2.3.2. Принадлежит ли цепочка x = (()())() языку, порождаемому грамматикой с правилами:

S -> SA|A
A -> (S)|()

2.3.3. Принадлежит ли цепочка x = 00011011 языку, порождаемому грамматикой с правилами:

S -> SS|A
A -> 0A1|S|01

2.3.4. Принадлежит ли цепочка x = 0111000 языку, порождаемому грамматикой с правилами:

S -> A0B|B1A
A -> BB|0
B -> AA|1

2.3.5. Верно ли соотношение a*cb* 2 L(G) для следующей грамматики G?

S -> Bab|aDa; A -> Dc|cA; B -> Sb|b;
D -> AB|aD.

2.3.6. Верно ли соотношение ab*c* 2 L(G) для следующей грамматики G?

S -> SAS|A; A -> Ac|Da|b; B -> DaD;
D -> ABD|AB.

2.3.7. Верно ли соотношение ca*b* 2 L(G) для следующей грамматики G?

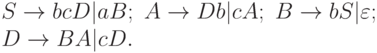
2.3.8. Верно ли соотношение c*ab* 2 L(G) для следующей грамматики G?

S -> ASS|A; A -> c|Ab|aD; B -> aDD;
D -> AB|BaB.

2.3.9. Пусть грамматика G определяется правилами

S -> AB; AB -> CBb; CB -> ABB;
A -> a; aB -> a:

Какому классу (по Хомскому) она принадлежит? Порождается ли L(G) грамматикой более узкого класса?

2.3.10. Пусть грамматика G определяется правилами

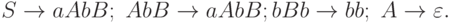
Какому классу (по Хомскому) она принадлежит? Порождается ли L(G) грамматикой более узкого класса?

2.3.11. Пусть грамматика G определяется правилами

Какому классу (по Хомскому) она принадлежит? Порождается ли L(G) грамматикой более узкого класса?

2.3.12. Пусть грамматика G определяется правилами

S -> AB; AB -> aDB; DB -> ABB; B -> b; Ab -> b.

Какому классу (по Хомскому) она принадлежит? Порождается ли L(G) грамматикой более узкого класса?

2.3.13. Какому классу по Хомскому принадлежит:

а) Грамматика с правилами:

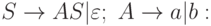
б) Язык, порождаемый этой грамматикой?

2.3.14. Какому классу по Хомскому принадлежит:

а) Грамматика с правилами:

S -> AB; AB -> aABB; B -> b; A -> a;

б) Язык, порожденный этой грамматикой?

2.3.15. Какому классу по Хомскому принадлежит:

а) Грамматика с правилами:

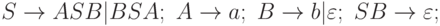
б) Язык, порожденный этой грамматикой?

2.3.16. Какому классу по Хомскому принадлежит:

а) Грамматика с правилами:

S -> AcBs; A -> AcA|B; B -> a|b;

б) Язык, порождeнный этой грамматикой?

2.3.17. Сколько существует различных выводов цепочки baaaab, принадлежащей языку, порождаемому грамматикой с правилами:

S -> bAb; A -> AA|a

2.3.18. Построить праволинейные грамматики для языков, состоящих из:

а) идентификаторов произвольной длины, начинающихся с буквы;

б) идентификаторов, содержащих от 1 до 6 символов и начинающихся с букв I, J, K, L, M, N;

в) вещественных констант;

г) всех цепочек из нулей и единиц, имеющих:

- чeтное число нулей и чeтное число единиц;

- либо нечeтное число нулей и нечeтное число единиц.