Задачи по разделам курса
Лексический анализ
Регулярные множества и выражения
3.1.1. Показать, что множества, соответствующие двум данным регулярным выражениям, совпадают,
1) (a*b)c и a*(bc); 2) a*b и b + aa*b; 3) b(b + ab)*a и b(b*ab)*b*a; 4) b(ab + b)* и bb*a(bb*a)*:
3.1.2. Заменить каждое из следующих выражений эквивалентным, в котором не используются знак "+":
1) (a + b)*; 2) (a + bb + ba)*; 3) (a + (bb + ab)*)*:
3.1.3. Найти регулярные выражения, обозначающие языки, все слова которых - элементы множества {0, 1}*:

3.1.4. Является ли язык, состоящий из всех цепочек из 0 и 1, не содержащих подцепочки 010, регулярным?
3.1.5. Является ли язык, состоящий из всех цепочек из 0 и 1, содержащих чeтное число 0 и нечeтное - 1, регулярным?
3.1.6. Является ли язык, состоящий из всех цепочек чeтной длины в алфавите {fa, b, c}, регулярным?
3.1.7. Регулярен ли

3.1.8. Определить язык, состоящий из всех идентификаторов, с помощью:
а) регулярного выражения; б) леволинейной грамматики; в) конечного автомата; г) праволинейной грамматики.
3.1.9. Будет ли регулярным язык 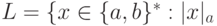 четно и |x|b нечетно}?
четно и |x|b нечетно}?
3.1.10. Построить праволинейную грамматику, порождающую язык L всех слов в алфавите {0, 1}, содержащих чeтное число единиц и нечeтное число нулей. Будет ли она однозначной?
3.1.11. Построить регулярное выражение для языка LR, где L - язык всех слов в алфавите {0, 1}, содержащих чeтное число единиц и нечeтное число нулей.
Конечные автоматы
3.2.1. Какой язык допускается конечным автоматом 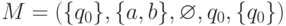 ?
?
3.2.2. Построить недетерминированный конечный автомат, допускающий цепочки в алфавите {1, 2}, у которых последний символ цепочки уже появлялся в ней раньше. Построить эквивалентный детерминированный конечный автомат. Построить аналогичные конечные автоматы в алфавите {1, 2, 3}.
3.2.3. Построить конечный автомат, допускающий язык 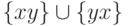 , где
, где  .
.
3.2.4. Построить детерминированный конечный автомат, допускающий язык L всех слов в алфавите {0, 1}, содержащих чeтное число единиц и нечeтное число нулей;
Алгоритмы построения конечных автоматов
3.3.1. Для регулярного выражения над алфавитом T = {a, b} построить эквивалентный детерминированный конечный автомат:
а) b(ba|b)*|b б) (ab|b)*ba|ab в) (a|b)*ba(a|b) г) (a|b)*ab(a|b)* д) a(ab|b)*|ba е) (ba|b)*ab|ba ж) (a*b)*ab*a з) (a|b)*(a|b)(a|b(a|b)
Лексический анализ
Регулярные множества и их представления
3.4.1. Будет ли регулярным язык  не содержит подцепочки aba }?
не содержит подцепочки aba }?
3.4.2. Возможно ли построить регулярную грамматику, порождающую язык, включающий в себя все непустые цепочки из 0 и 1, не содержащие трeх 1 подряд?
Алгебраические свойства регулярных множеств. Лемма о разрастании.
3.5.1. Будут ли регулярными следующие языки в алфавите {a}:
а) 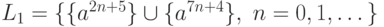 ;
;
б) 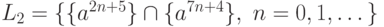 ;
;
в) 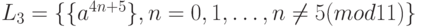 ;
;
д) 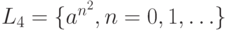 .
.
3.5.2. Будут ли регулярными следующие языки в алфавите 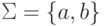 :
:
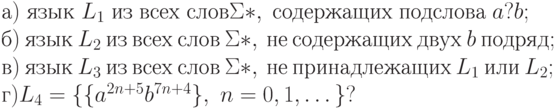
3.5.3. Задается ли язык {anbm|n  m
m  1} регулярным
выражением?
1} регулярным
выражением?
3.5.4. Является ли грамматика с правилами:
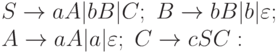
праволинейной грамматикой?
